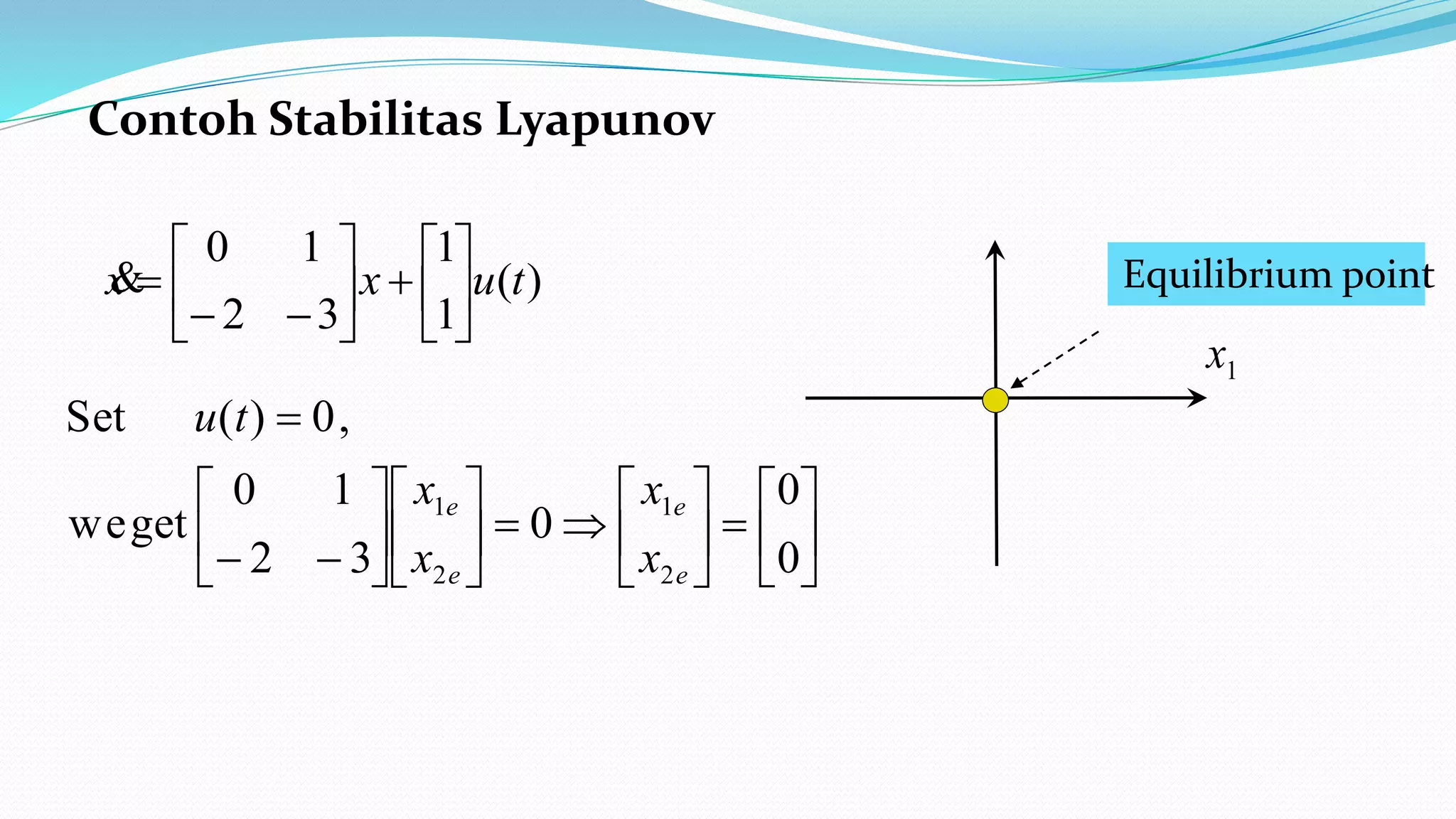
Dokumen ini membahas tentang stabilitas Lyapunov, sebuah metode untuk menganalisis kestabilan sistem linier dan nonlinier. Terdapat penjelasan mengenai stabilitas asimptotik baik lokal maupun global, serta bentuk kuadrat dan hermitian Lyapunov. Metode kedua Lyapunov juga dijelaskan beserta syarat-syarat untuk mencapai kestabilan asimptotik global.

1. Stabilitas Lyapunov
Nama : Trisni Wulansari / 1410501026
Dosen Pengampu : R. Suryoto Edy Raharjo, S.T., M.Eng.
Teknik Elektro, Fakultas Teknik Universitas Tidar

2. Outline
Pengertian Stabilitas Lyapunov
Stabilitas secara asimptotik
Stabilitas secara asimptotik bersifat lokal ataupun global
Penyajian Diagram Kestabilan dan Ketidakstabilan.
Bentuk kuadrat Lyapunov
Bentuk Hermitian Lyapunov
Metode kedua Lyapunov

3. Stabilitas Lyapunov
Aleksandr Mikhailovich Lyapunov merupakan penemu materi lyapunov.
Stabilitas Lyapunov merupakan jenis metode yang digunakan untuk menyelidiki
kinerja (terutama kestabilan) sistem linier maupun nonlinier , yang :
• Tak berubah dengan waktu maupun berubah dengan waktu
• Dengan order rendah maupun order tinggi.
hanya berlaku bagi sistem nonlinier , dengan sifat nonlinieritas tidak diskontinyu
atau mendadak perubahannya .

4. Stabilitas secara asimptotik
Sistem dengan dinamika
dapat dikatakan stabil secara asimptotik jika terdapat satu fungsi V(x) , yang
disebut kandidat fungsi Lyapunov, yang memenuhi sifat-sifat berikut ini.
,
, dan hanya bernilai nol untuk
Pada saat waktu t menjadi tak berhingga (menuju kekekalan), maka semua state
pada sistem tersebut sudah menuju ke titik kesetimbangan, dan pada saat itu,
gangguan sebesar apapun akan mengakibatkan pergeseran (lokal) yang pada
akhirnya dengan berjalannya waktu, semua state pada sistem bergerak kembali
menuju kesetimbangan.

5. Stabilitas secara asimptotik bersifat lokal ataupun global
1. Lokal, bila hanya berlaku untuk nilai-nilai state awal (initial state) di sekitar
titik kesetimbangan (the neighborhood of the equilibrium point).
2. Global, bila untuk semua nilai-nilai state awal, semua state akan bergerak
menuju 1 titik kesetimbangan yang sama.
Jikakeadaanasimptotikberlakuuntuksemuakeadaantitikawaltrayektori,makak
eadaankesetimbangantersebutstabilasimptotikglobal.
Keadaankesetimbanganxedarisistemdisebutstabilasimptotikglobaljikakeadaa
nsetimbangtersebutstabil,danjikasetiapjawabkonvergenkexedenganmembesar
nyawaktutmenunjutakhingga.
Syaratyangperluuntukkestabilanasimptotikglobaladalahbahwahanyaadasatu
keadaankesetimbangandalamseluruhkeadaan

6. Penyajian Diagram Kestabilan dan Ketidakstabilan.
Gambar: Kondisi yang menggambarkan
pergerakan perluru setimbangstabil
Terlihat pada gambar, menunjukkan
lintasan peluru dari kondisi awal x0dengan
batas keadaan awal S(δ).
Kondisi setimbang stabil sesuai hukum Lyapunov.

7. Penyajian Diagram Kestabilan dan Ketidakstabilan.
Kondisikeadaan setimbang secara garis
lurus
pergerakan peluru dari titik awal x0pada
daerah batas keadaan awal S(δ) menuju ke
daerah ini kembali, pergerakan ini
dikatakan sebagai kondisi setimbang secara
garis lurus

8. Penyajian Diagram Kestabilan dan Ketidakstabilan.
Kondisi tidak stabil
pergerakan peluru dari kondisi awal
x0menuju keluar dari batas kesetimbangan
S(ε) menunjukkan bahwa kondisi setimbang
tidak stabil.

9. Bentuk kuadrat Lyapunov
Beberapa contoh dari fungsi skalar Lyapunov yang menunjukkan sifat – sifat
seperti disebutkan diatas,

10. Bentuk kuadrat Lyapunov
Untuk memahami bahwa fungsi skalar dari Lyapunov, menunjukkan suatu
kondisi kestabilan, maka dinyatakan dalam bentuk kuadrat, dalam persamaan
berikut,
X merupakan vektor bernilai real, dan P adalah matriks simetri bernilai real.

11. Bentuk Hermitian Lyapunov
Jika x adalah n – vektor bernilai kompleks dan P adalah sebuah matriks
Hermitian, maka bentuk kuadrat kompleks dikatakan sebagai bentuk
Hermitian.

12. Metode kedua Lyapunov
Teorema 1 : Jika diketahui, suatu sistem dinyatakan dalam bentuk :
Dimana : f(0,t) = 0 untuk sembarang t. Jika ada suatu parameter V(x,t) yang
mempunyai turunan parsial pertama kontinyu dan memenuhi syarat :
• V(x,t) definit positif
• definit negatif
Maka keadaan kesetimbangan di titik asal adalah stabil asimptotik secara
uniform. Jika ternyata V(x,t) → ~ untuk ║x║→ ~, maka keadaan kesetimbangan
di titik asal adalah stabil asimptotik global secara uniform.

13. Metode kedua Lyapunov
Teorema 2 : Jika diketahui, suatu sistem dinyatakan dalam bentuk :
untuk sembarang t
.Jika ada suatu parameter V(x,t) yang mempunyai turunan parsial pertama
kontinyu dan memenuhi syarat :
• V(x,t) definit positif
• definit negatif
tidak terjadi nol pada t ≥ t0 , untuk t0 dan x0 dimana
Φ(t, x0 , t0 ) menyatakan trayektori atau jawab dengan titik awal di
x0 pada t0 , maka keadaan kesetimbangan di titik asal dari sistem
adalah stabil asimptotik global secara uniform.

14. Contoh Stabilitas Lyapunov
)(
1
1
32
10
tuxx 







































0
0
0
32
10
getwe
,0)(Set
2
1
2
1
e
e
e
e
x
x
x
x
tu
1x
Equilibrium point

15. Daftar Pustaka
•https://teknikpengaturan.wordpress.com/2009/10/07/mengapa-lyapunov-
mengatakan-there-exists-dalam-teori-stabilitasnya/
•http://eprints.undip.ac.id/31376/
•http://stanford.edu/class/ee363/lectures/lyap.pdf
•http://share.its.ac.id/pluginfile.php/40669/mod_resource/content/3/8.9%20Anal
isa%20Kestabilan%20Lyapunov.pdf
•https://en.wikipedia.org/wiki/Lyapunov_stability
•http://www.mnurq.ga/2014/11/persamaan-dan-fungsi-lyapunov.html

16. Terima Kasih
231116