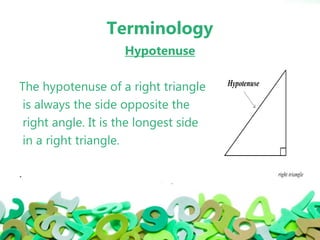
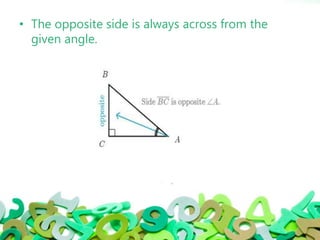
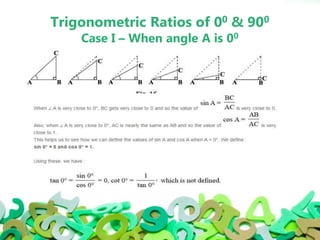
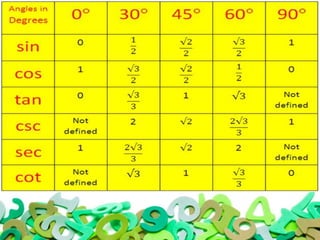
Trigonometry is a branch of mathematics that studies relationships involving lengths and angles of triangles. It was originated by Hipparchus around 140BC to study the motion of planets and solar/lunar eclipses. There are three basic trigonometric functions: sine, cosine, and tangent. Sine is the ratio of the opposite side to the hypotenuse. Cosine is the ratio of the adjacent side to the hypotenuse. Tangent is the ratio of the opposite side to the adjacent side. Trigonometry has many applications in fields like astronomy, navigation, surveying, and defense.

1. Topic – Introduction to
Trigonometry
By : Ravikumar D
Msc(Mathematics).

3. Introduction to Trigonometry
• Branch of Mathematics that deals with the
triangles, mostly with right triangles, used
in finding relationship between sides &
angles.

4. Definition
• Branch of mathematics that studies
relationships involving lengths
and angles of triangles.

5. Origin & Purpose of Trigonometry
Name - Hipparchus, known as father of
trigonometry
Place - Turkey
Year -140BC
Need - To find the motion of the planets, and the
solar and lunar eclipses

6. Overview
Trigonometric Functions
There are three basic trigonometric functions
which are :-
1. Sine Function (Sin)
2. Cosine Function (Cos)
3. Tangent Function (Tan)

7. Terminology
Hypotenuse
The hypotenuse of a right triangle
is always the side opposite the
right angle. It is the longest side
in a right triangle.
.

8. • The opposite side is always across from the
given angle.

9. • Angle of elevation
• The angle of elevation of an object as seen by an
observer is the angle between the horizontal and
the line from the object to the observer's eye
(the line of sight).

10. Basics Understanding of
Trigonometry

11. Sine Function
• Sine function (sin), defined as the ratio of the
side opposite the angle to the hypotenuse.
• SOH - Sine is Opposite over Hypotenuse

12. Cosine Function
• Cosine function (cos), defined as the ratio of
the adjacent leg to the hypotenuse.
• CAH - Cosine is Adjacent over Hypotenuse

13. Tangent Function (Tan)
• Tangent function (tan), defined as the ratio of
the opposite leg to the adjacent leg.
• Tangent - Opposite over Adjacent

15. Reciprocal Functions
• The cosecant or cosec(A), is the reciprocal of
sin(A); i.e. the ratio of the length of the
hypotenuse to the length of the opposite side

16. • The secant sec(A) is the reciprocal of cos(A); i.e.
the ratio of the length of the hypotenuse to the
length of the adjacent side

17. • The cotangent cot(A) is the reciprocal of tan(A);
i.e. the ratio of the length of the adjacent side to
the length of the opposite side

19. Finding the value of Trigonometric
Functions

22. • Similarly

23. Trigonometric Ratios of 00 & 900
Case I – When angle A is 00

24. Case II – When angle A is 900

26. Example :-
In Δ PQR, right-angled at Q, PQ = 3 cm and PR = 6 cm. Determine ∠
QPR and ∠ PRQ.
Solution :-

27. Example :-Evaluate the following
Solution :-

28. Trigonometrical Ratios
of Complementary
Angles

30. Example

31. Trigonometric Identities

32. Example

33. Applications in Real Life
• In ancient time it was used for astronomy
in finding distance of stars
• Finding radius of earth
• Finding height of hills, buildings, trees
• Navigation – Airplane, Ships etc.
• Defense