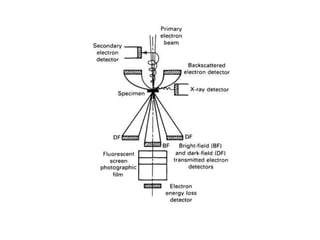
The transmission electron microscope can be used to image microstructural features at high magnifications, perform elemental analysis, and determine crystal structures. Samples must be thinly sectioned or ion milled to be electron transparent. Imaging techniques like bright field and dark field are used to reveal structural features based on diffraction contrast. Selected area diffraction patterns can be indexed to identify crystal structures and orientations. The transmission electron microscope thus provides valuable microscopic and crystallographic information about materials at high resolution.

1. Transmission Electron
Microscope

2. General Uses
• Imaging of micro structural features at 1000 to 450000 X.
Resolution - ˂ 1 nm
• Qualitative and Quantitative elemental analysis
• Crystal structure and Orientation determination
• Lattice imaging of crystals with inter planar spacing

3. Applications
• High magnification characterization of the microstructure
of metals, ceramics, geologic materials, polymers and
biological materials
• Identification (Composition and Crystal structure) of
inorganic phases, precipitates and contaminants

4. Samples
• Solids – Metals, Ceramics, Minerals, Polymers,
biological etc.
• Size: ~ 5 µm thick, 3mm diam disk
• Preparation: Specimens must be sectioned and electro-
thinned or ion milled to produce regions that permit
transmission of the electron beam
• Powder samples are often dispersed on a thin carbon
substrate

5. Limitations
• Sample preparation is tedious and development of a suitable
procedure may take weeks
• Elemental microanalysis:
• Electron Diffraction:
Typical minimum size of the region
analyzed is 30 nm in diameter
Sensitivity- ~ 0.5 to 1 wt %
Accuracy of quantification – 5 to 15 %
Quantification possible for atomic
number ≥ 11
Minimum size of region analyzed : ~ 30 nm
Crystal structure identification is limited to phases or compounds
tabulated in powder difraction file

6. Introduction
• It is unique among materials characterization
techniques because of simultaneous
examination of micro-structural features through
high resolution imaging, chemical and
crystallographic information from small regions
of the specimen

7. Principles
• Formation of diffraction patterns and images in
TEM : Kinematic theory of electron diffraction

8. Instrumentation
• Electron Optics:
• Electron Beam Specimen Interaction
• Signal Detectors
Electron Guns
Electromagnetic Lenses
Elastic Scattering
Inelastic scattering
Electron scattering volume

11. 2q ≈ sin 2q = R/L
l = 2d sin q ≈ d (2q)
R/L = l/d
Rd = lL
L is "camera length"
lL is "camera constant"
image plane
specimen
λ = wavelength of electrons ( 0.0037 nm and 0.0025 for 100 and 200 keV electrons
respectively
d = interplanar spacing for the family of diffracting planes
Θ= diffracting angle

12. Rules for Diffraction
• The diffraction of atomic plane is a function of
crystal structure.
• All planes can diffract in simple (Bravais) lattice.
• Only planes in which h and k (of the Miller
indices) are both odd or even can diffract in a
base-centered lattice
• Only planes in which (h+k+l) is even can diffract in
body-centered Bravais lattice.
• Only planes in which h, k and l are all even or odd
can diffract in a face-centered Bravais lattice.

13. Selected area diffraction patern (SADP)
• The selected-area aperture is used to limit the
area of the specimen for diffraction.
• The minimum area from which SADP is
generated is ~0.5 μm diameter.
• Three types of electron diffraction patterns
can be generated:
– Ring pattern
– Spot pattern
– Kikuchi line pattern

14. Diffraction
Get pattern of spots around transmitted beam from one grain (crystal)

15. Diffraction
Symmetry of diffraction pattern reflects
symmetry of crystal around beam direction
Why does 3-fold diffraction pattern look hexagonal?
[111] in cubic [001] in hexagonal
Example:
6-fold in hexagonal, 3-fold in cubic

16. Diffraction
Note: all diffraction patterns
are centrosymmetric,
even crystal structure is not
centrosymmetric (Friedel's
law)
Some 0-level patterns thus
exhibit higher rotational
symmetry than structure has
P cubic reciprocal lattice
layers along [111] direction
0-level
l = +1 level
l = -1 level

17. Diffraction
Cr23C6 - F cubic
a = 10.659 Å
Ni2AlTi - P cubic
a = 2.92 Å

18. Indexing electron diffraction patterns
Measure R-values for at least 3 reflections

19. Indexing electron diffraction patterns

20. Indexing electron diffraction patterns
Index other reflections by vector sums, differences
Next find zone axis from cross product of any two (hkl)s
(202) x (220) ——> [444] ——> [111]

21. Indexing electron diffraction patterns
Find crystal system, lattice parameters, index pattern, find zone axis
ACTF!!! Note symmetry - if cubic, what direction
has this symmetry (mm2)?
Reciprocal lattice unit cell
for cubic lattice is a cube

22. Polycrystalline regions
polycrystalline BaTiO3
spotty Debye rings

23. Indexing electron diffraction patterns - polycrystalline regions
Same as X-rays – smallest ring - lowest q - largest d
Hafnium (铪)

24. Indexing electron diffraction patterns - comments
Helps to have some idea what phases present
d-values not as precise as those from X-ray data
Systematic absences for lattice centering and other translational
symmetry same as for X-rays
Intensity information difficult to interpret

25. Sources of contrast
Diffraction contrast - some grains diffract more strongly than others;
defects may affect diffraction
Mass-thickness contrast - absorption/
scattering. Thicker areas or mat'ls w/
higher Z are dark

26. Bright field imaging
Only main beam is used. Aperture in back focal plane blocks diffracted
beams
Image contrast mainly due to subtraction of intensity from the main beam
by diffraction

27. Bright field imaging
Only main beam is used. Aperture in back focal plane blocks diffracted
beams
Image contrast mainly due to subtraction of intensity from the main beam
by diffraction

28. Bright field imaging
Only main beam is used. Aperture in back focal plane blocks diffracted
beams
Image contrast mainly due to subtraction of intensity from the main beam
by diffraction

29. Bright field imaging
Only main beam is used. Aperture in back focal plane blocks diffracted
beams
Image contrast mainly due to subtraction of intensity from the main beam
by diffraction

30. What else is in the image?
Many artifacts
surface films
local contamination
differential thinning
others
Also get changes in image because of
annealing due to heating by beam

31. Dark field imaging
Instead of main
beam, use a
diffracted beam
Move aperture to
diffracted beam or
tilt incident beam

32. Dark field imaging
Instead of main beam, use a diffracted beam
Move aperture to diffracted beam or tilt incident beam
strain field contrast

33. Dark field imaging
Instead of main beam, use a diffracted beam
Move aperture to diffracted beam or tilt incident beam

34. Lattice imaging
Use many diffracted beams
Slightly off-focus
Need very thin specimen region
Need precise specimen alignment
See channels through foil
Channels may be light or dark in image
Usually do image simulation to
determine features of structure

35. Examples
M23X6 (figure at top
left).
L21 type b'-Ni2AlTi
(figure at top center).
L12 type twinned g'-
Ni3Al (figure at bottom
center).
L10 type twinned NiAl
martensite (figure at
bottom right).