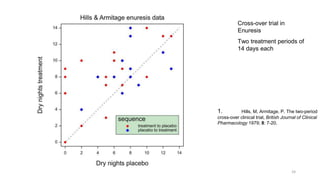
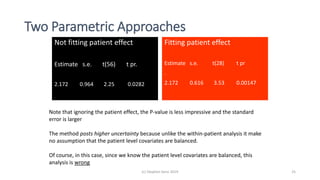
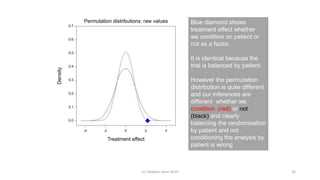
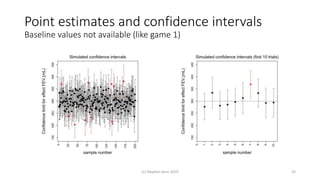
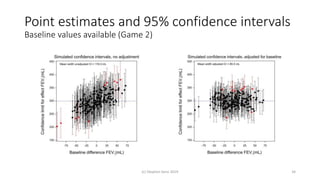
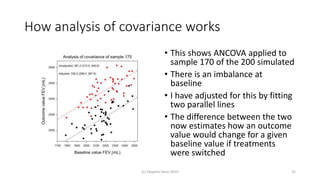
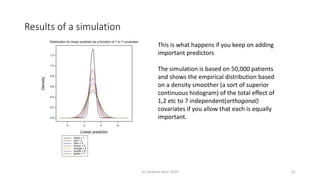
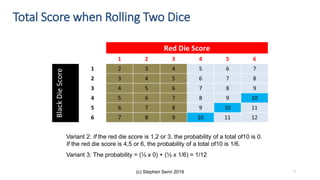
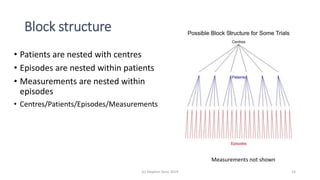
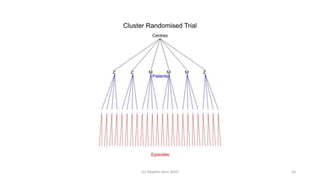
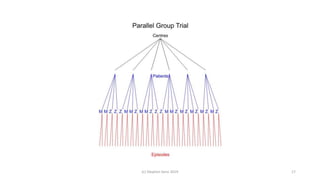
Randomisation balances both known and unknown factors that influence outcomes between treatment groups on average. Conditioning the analysis on available baseline covariates further reduces uncertainty by accounting for imbalances. While there are many potential covariates, their combined influence is bounded; randomisation thus remains important for accounting for unknown factors. Correct analysis requires matching the randomisation design to the analysis to make valid statistical inferences.

1. Understanding
Randomisation
Stephen Senn, Edinburgh
(c) Stephen Senn 2019 1

2. (c) Stephen Senn 2019 2
An anniversary
• RA Fisher 1890-1962
• Statistician at Rothamsted agricultural
station 1919-1933
• Most influential statistician ever
• Also a major figure in evolutionary
biology
• Educated Harrow and Cambridge
• Developed theory of small sample
inference and many modern concepts
• Likelihood, variance, sufficiency, ANOVA
• Developed theory of experimental
design
• Blocking, Replication, Randomisation
This is the 100th anniversary of Fisher’s
arrival at Rothamsted research station

3. Outline
• Preliminary
• A game of two dice
• What is randomisation and how does it work?
• Illustration using three kinds of randomised trial
• Illustration using a famous cross-over trial
• Understanding conditioning
• Analysis of covariance explained through simulation
• Two common criticisms
• Conclusions?
(c) Stephen Senn 2019 3

4. A game of two dice
Roll call
(c) Stephen Senn 2019 4

5. (c) Stephen Senn 2019
• Two dice are rolled
– Red die
– Black die
• You have to call correctly the probability of a total score of 10
• Three variants
– Game 1 You call the probability and the dice are rolled
together
– Game 2 the red die is rolled first, you are shown the score
and then must call the probability
– Game 3 the red die is rolled first, you are not shown the
score and then must call the probability
Game of Chance
5

6. (c) Stephen Senn 2019
Total Score when Rolling Two Dice
Variant 1. Three of 36 equally likely results give a 10. The probability is 3/36=1/12.
6

7. (c) Stephen Senn 2019
Variant 2: If the red die score is 1,2 or 3, the probability of a total of10 is 0.
If the red die score is 4,5 or 6, the probability of a total of10 is 1/6.
Variant 3: The probability = (½ x 0) + (½ x 1/6) = 1/12
Total Score when Rolling Two Dice
7

8. The morals
Dice games
• You can’t treat game 2 like game 1
• You must condition on the information
received
• You must use the actual data from the red die
• You can treat game 3 like game 1
• You can use the distribution in probability
that the red die has
Inference in general
• You can’t use the random behavior of
a system to justify ignoring
information that arises from the
system
• That would be to treat game 2 like game 1
• You can use the random behavior of
the system to justify ignoring that
which has not been seen
• You are entitled to treat game 3 like game 1
(c) Stephen Senn 2019 8

9. What does randomisation do?
Mastering uncertainty
(c) Stephen Senn 2019 9

10. Some jargon 1
• Outcomes
• What we measure at the end of a trial and regard as being relevant to judging the
effect of treatment
• Treatment
• What the experimenter varies
• Caution: Sometimes we refer to treatment as being a factor that has two or more levels (for
example beta-blocker or placebo) but sometimes, confusingly we may refer to one of the
levels as treatments .(For example treatment versus placebo)
• Analogy: geneticists sometimes use gene to mean locus and sometimes to mean allele . (The
gene for earwax or the gene for wet-type earwax.)
• Covariate
• Something else that may predict outcomes and can be measured before the trial
starts
(c) Stephen Senn 2019 10

11. Some jargon 2
• Unit
• That which is treated from the experimental point of view: usually patients,
but it could be centres or it might be episodes in the life of a patient
• Allocation algorithm
• The way that treatments are allocated to units (for example to patients)
• Blocking factor (or sometimes block)
• A particular type of covariate that can be recognised and accounted for in the
allocation process
• For example, centre We can choose to ‘block’ treatments by centre. We try make sure
that (say) equal numbers of patients within a given centre receive two treatments that
are being compared
(c) Stephen Senn 2019 11

12. What does the Rothamsted approach do?
• Matches the allocation procedure to the analysis. You can either
regard this as meaning
• The randomisation you carried out guides the analysis
• The analysis you intend guides the randomisation
• Or both
• Either way, the idea is to avoid inconsistency
• Regarding something as being very important at the allocation stage but not
at the analysis stage is inconsistent
• Permits you not only to take account of things seen but also to make
an appropriate allowance for things unseen
• Die analogy is that it makes sure that the game is a fair one
(c) Stephen Senn 2019 12

13. Trial in asthma
Basic situation
• Two beta-agonists compared
• Zephyr(Z) and Mistral(M)
• Block structure has several levels
• Different designs will be investigated
• Cluster
• Parallel group
• Cross-over Trial
• Each design will be blocked at a different
level
• NB Each design will collect
6 x 4 x 2 x 7 = 336 measurements of Forced
Expiratory Volume in one second (FEV1)
Block structure
Level Number
within higher
level
Total
Number
Centre 6 6
Patient 4 24
Episodes 2 48
Measurements 7 336
(c) Stephen Senn 2019 13

14. Block structure
• Patients are nested with centres
• Episodes are nested within patients
• Measurements are nested within
episodes
• Centres/Patients/Episodes/Measurements
(c) Stephen Senn 2019 14
Measurements not shown

15. Possible designs
• Cluster randomised
• In each centre all the patients either receive Zephyr (Z) or Mistral (M) in both
episodes
• Three centres are chosen at random to receive Z and three to receive M
• Parallel group trial
• In each centre half the patients receive Z and half M in both episodes
• Two patients per centre are randomly chosen to receive Z and two to receive
M
• Cross-over trial
• For each patient the patient receives M in one episode and Z in another
• The order of allocation, ZM or MZ is random
(c) Stephen Senn 2019 15

16. (c) Stephen Senn 2019 16

17. (c) Stephen Senn 2019 17

18. (c) Stephen Senn 2019 18

19. Null (skeleton) analysis of variance with Genstat ®
Code Output
(c) Stephen Senn 2019 19
BLOCKSTRUCTURE Centre/Patient/Episode/Measurement
ANOVA

20. Full (skeleton) analysis of variance with Genstat ®
Additional Code Output
(c) Stephen Senn 2019 20
TREATMENTSTRUCTURE Design[]
ANOVA
(Here Design[] is a pointer with values corresponding
to each of the three designs.)

21. The bottom line
• The approach recognises that things vary
• Centres, patients episodes
• It does not require everything to be balanced
• Things that can be eliminated will be eliminated by design
• Cross-over trial eliminates patients and centres
• Parallel group trial eliminates centres
• Cluster randomised eliminates none of these
• The measure of uncertainty produced by the analysis will reflected
what cannot be eliminated
• This requires matching the analysis to the design
(c) Stephen Senn 2019 21

22. A genuine example ( a real trial)
Hills and Armitage 1979
• A cross-over trial of enuresis
• Patients randomised to one of two sequences
• Active treatment in period 1 followed by placebo in period 2
• Placebo in period 1 followed by active treatment in period 2
• Treatment periods were 14 days long
• Number of dry nights measured
(c) Stephen Senn 2019 22

23. Important points to note
• Because every patient acts as his own control all patient level
covariates (of which there could be thousands and thousands) are
perfectly balanced
• Differences in these covariates can have no effect on the difference
between results under treatment and the results under placebo
• However, period level covariates (changes within the lives of patients)
could have an effect
• My normal practice is to fit a period effect as well as patients effects,
however, I shall omit doing so to simplify
• The parametric analysis then reduces to what is sometimes called a
matched pairs t-test
(c) Stephen Senn 2019 23

24. Cross-over trial in
Enuresis
Two treatment periods of
14 days each
1. Hills, M, Armitage, P. The two-period
cross-over clinical trial, British Journal of Clinical
Pharmacology 1979; 8: 7-20.
(c) Stephen Senn 2019 24

25. Two Parametric Approaches
Not fitting patient effect
Estimate s.e. t(56) t pr.
2.172 0.964 2.25 0.0282
Fitting patient effect
Estimate s.e. t(28) t pr
.
2.172 0.616 3.53 0.00147
(c) Stephen Senn 2019
Note that ignoring the patient effect, the P-value is less impressive and the standard
error is larger
The method posts higher uncertainty because unlike the within-patient analysis it make
no assumption that the patient level covariates are balanced.
Of course, in this case, since we know the patient level covariates are balanced, this
analysis is wrong
25

26. Blue diamond shows
treatment effect whether
we condition on patient or
not as a factor.
It is identical because the
trial is balanced by patient.
However the permutation
distribution is quite different
and our inferences are
different whether we
condition (red) or not
(black) and clearly
balancing the randomisation
by patient and not
conditioning the analysis by
patient is wrong
(c) Stephen Senn 2019 26

27. The two permutation* distributions summarised
Summary statistics for Permuted difference no
blocking
Number of observations = 10000
• Mean = -0.00319
• Median = -0.0345
• Minimum = -3.621
• Maximum = 3.690
• Lower quartile = -0.655
• Upper quartile = 0.655
Standard deviation = 0.993
P-value for observed difference 0.0344
(Parametric P-value 0.0282)
*Strictly speaking, these are randomisation
distributions
Summary statistics for Permuted difference
blocking
Number of observations = 10000
• Mean = -0.00339
• Median = 0.0345
• Minimum = -2.793
• Maximum = 2.517
• Lower quartile = -0.517
• Upper quartile = 0.517
P-value for observed difference 0.001
(Parametric P-value 0.00147)
(c) Stephen Senn 2019 27

28. What happens if you balance but don’t
condition?
Approach Variance of estimated
treatment effect over all
randomisations*
Mean of variance of
estimated treatment effect
over all randomisations*
Completely randomised
Analysed as such
0.987 0.996
Randomised within-patient
Analysed as such
0.534 0.529
Randomised within-patient
Analysed as completely
randomised
0.534 1.005
*Based on 10000 random permutations
(c) Stephen Senn 2019 28
That is to say, permute values respecting the fact that they come from a cross-over but analysing them as if
they came from a parallel group trial

29. The Shocking Truth
• The validity of conventional analysis of randomised trials does not
depend on covariate balance
• It is valid because they are not perfectly balanced
• An allowance is already made for things being unbalanced
• If they were balanced the standard analysis would be wrong
• Like an insurance broker forbidding you to travel abroad in the policy but
calculating your premiums on the assumption that you will
(c) Stephen Senn 2019 30

30. Understanding conditioning
Correcting for bias implies correcting for variance
(c) Stephen Senn 2019 31

31. A simulating example
• I am going to simulate 200 clinical trials
• Trials are of a bronchodilator against placebo.
• Simple randomisation of 50 patients to each arm
• I shall have values at outcome and values at baseline
• Forced expiratory volume in one second (FEV1) in mL
• Parameter settings
• True mean under placebo 2200 mL
• Under bronchodilator 2500 mL
• Treatment effect is 300 mL
• SD at outcome and baseline is 150 mL
• Correlation is 0.7
(c) Stephen Senn 2019 32

32. Point estimates and confidence intervals
Baseline values not available (like game 1)
(c) Stephen Senn 2019 33

33. Point estimates and 95% confidence intervals
Baseline values available (Game 2)
(c) Stephen Senn 2019 34

34. How analysis of covariance works
• This shows ANCOVA applied to
sample 170 of the 200 simulated
• There is an imbalance at
baseline
• I have adjusted for this by fitting
two parallel lines
• The difference between the two
now estimates how an outcome
value would change for a given
baseline value if treatments
were switched
(c) Stephen Senn 2019 35

35. Two common criticisms
First catch your carp
(c) Stephen Senn 2019 36

36. The criticisms
1. Since you are going to condition, who needs randomisation
2. Since there are indefinitely many confounders, something is bound
to be seriously imbalanced
(c) Stephen Senn 2019 37

37. Randomisation is superfluous
• The error is to assume that because you can’t use randomisation as a
justification for ignoring information it is useless
• It is useful for what you don’t see
• Knowing that the two-dice game is fairly run is important even though
the average probability is not relevant to game two
• Average probabilities are important for calibrating your inferences
• Your conditional probabilities must be coherent with your marginal ones
• See the relationship between the games
(c) Stephen Senn 2019 38

38. Indefinite irrelevance
• One sometimes hears that the fact that there are indefinitely many
covariates means that randomisation is useless
• This is quite wrong
• It is based on a misunderstanding that variant 3 of our game should not
be analysed like variant 1
• I showed you that it should
(c) Stephen Senn 2019 39

39. You are not free to imagine anything at all
• Imagine that you are in control of all
the thousands and thousands of
covariates that patients will have
• You are now going to allocate the
covariates and their effects to patients
• As in a simulation
• If you respect the actual variation in
human health that there can be you
will find that the net total effect of
these covariates is bounded
𝑌 = 𝛽0 + 𝑍 + 𝛽1 𝑋1 + ⋯ 𝛽 𝑘 𝑋 𝑘 + ⋯
Where Z is a treatment indicator and the X are
covariates. You are not free to arbitrarily assume any
values you like for the Xs and the 𝛽𝑠 because the
variance of Y must be respected.
(c) Stephen Senn 2019 40

40. Results of a simulation
(c) Stephen Senn 2019 41
This is what happens if you keep on adding
important predictors
The simulation is based on 50,000 patients
and shows the empirical distribution based
on a density smoother (a sort of superior
continuous histogram) of the total effect of
1,2 etc to 7 independent(orthogonal)
covariates if you allow that each is equally
important.

41. The essence of the error
• The error is to imagine that a sum of an indefinite number of terms
cannot be bounded
• However, Zeno notwithstanding, we do not consider that the sum of
the series 1, 1/2, 1/4 …..1/2n-1 etc is unbounded
• 1,+1/2+ 1/4+ …..1/2n-1 is less than 2, however large n is
• Thus, to assume that an indefinite series implies an indefinite total
effect is a fallacy
• The total effect is bounded and its value is estimated by looking at the
variation within groups of the outcome
(c) Stephen Senn 2019 42

42. The importance of ratios
• In fact from one point of view there is only one covariate that matters
• potential outcome
• If you know this, all other covariates are irrelevant
• And just as this can vary between groups in can vary within
• The t-statistic is based on the ratio of differences between to variation
within
• Randomisation guarantees (to a good approximation) the
unconditional behaviour of this ratio and that is all that matters for
what you can’t see (game 3)
(c) Stephen Senn 2019 43

43. Conclusions
Finally! The beginning of the end.
(c) Stephen Senn 2019 44

44. My ‘Philosophy’ of Clinical Trials
• Your (reasonable) beliefs dictate the model
• You should try measure what you think is important
• You should try fit what you have measured
• Caveat : random regressors and the Gauss-Markov theorem
• If you can balance what is important so much the better
• But fitting is more important than balancing
• Randomisation deals with unmeasured covariates
• You can use the distribution in probability of unmeasured covariates
• For measured covariates you must use the actual observed distribution
• Claiming to do ‘conservative inference’ is just a convenient way of hiding bad
practice
• Who thinks that analysing a matched pairs t as a two sample t is acceptable?
45(c) Stephen Senn 2019

45. My philosophy of approaching the philosophy
of randomisation
• The devil is in the detail
• Check that you understand
1. How randomisation is done
2. How randomised experiments are analysed
3. What the statistical theory of randomisation claims
• Check any verbal claims you make
1. Do the maths (don’t just say ‘Bayesian this, Bayesian that’, if you don’t really
know how Bayesian analysis works)
2. Ask yourself ‘can I simulate the problem I claim?’
(c) Stephen Senn 2019 46

46. Typical MRC* Stuff
‘The central telephone randomisation system used a minimisation algorithm to
balance the treatment groups with respect to eligibility criteria and other major
prognostic factors.’ (p24)
‘All comparisons involved logrank analyses of the first occurrence of particular
events during the scheduled treatment period after randomisation among all those
allocated the vitamins versus all those allocated matching placebo capsules (ie,
they were “intention-to treat” analyses).’ (p24)
1. (2002) MRC/BHF Heart Protection Study of cholesterol lowering
with simvastatin in 20,536 high-risk individuals: a randomised placebo-
controlled trial. Lancet 360:7-22
47(c) Stephen Senn 2019
The UK’s Medical Research Council

47. The Problem
• However, this seems to imply that in making inferences for
randomised clinical trials we must condition on everything we
observe
• All covariates must be in the model
• What is the effect on efficiency?
• Could it mean that more information is worse than less?
• That’s another talk
48(c) Stephen Senn 2019

48. A quote from a local hero
The use of random sampling is a device for obtaining apparently precise
objectivity but this precise objectivity is attainable, as always, only at the
price of throwing away some information (by using a Statistician’s
Stooge who knows the random numbers but does not disclose them)…
…But the use of sampling without randomization involves the pure
Bayesian in such difficult judgments that, at least if he is at all Doogian,
he might decide by Type II rationality, to use random sampling to save
time.
Jack Good, Good Thinking
50(c) Stephen Senn 2019 50

49. To sum up
• Randomisation makes a valuable contribution to handling
unobserved variables
• Randomisation does not guarantee balance of unobserved
variables
• This balance is not needed
• If it applied, conventional analyses would be invalid
• Randomisation is not an excuse for ignoring prognostic
covariates
• Some technical challenges remain but these are challenges of
modelling not randomisation per se
51(c) Stephen Senn 2019

50. Finally
I leave you with
this thought
Statisticians are always
tossing coins but do not
own many
52(c) Stephen Senn 2019