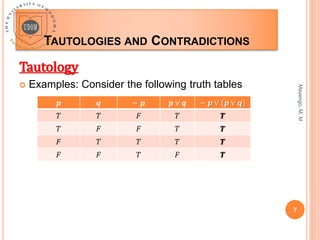
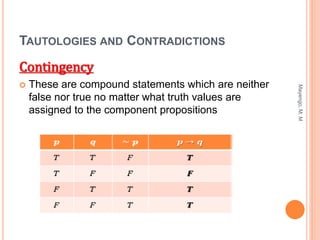
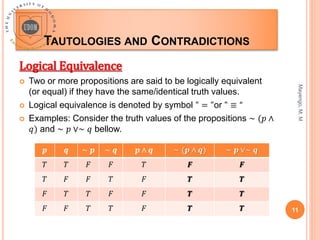
This document outlines the laws of algebra for propositional logic, including identities, commutative laws, associative laws, distributive laws, De Morgan's laws, and other logical equivalences. It defines tautologies as statements that are always true regardless of the truth values assigned to variables, and contradictions as statements that are always false. Examples of truth tables are provided to demonstrate tautologies, contradictions, and logical equivalence between statements. The document concludes by posing questions to classify logic formulas as tautologies, contradictions, or contingencies using truth tables and the laws of propositional logic.

1. LAWS OF ALGEBRA OF PREPOSITIONS
Mayengo,
M.
M
1
Identities
 𝑝 ∨ 𝑝 ≡ 𝑝
 𝑝 ∨ 𝑇 ≡ 𝑇
 𝑝 ∨ 𝐹 ≡ 𝑝
 𝑝 ∧ 𝑝 ≡ 𝑝
 𝑝 ∧ 𝑇 ≡ 𝑝
 𝑝 ∧ 𝐹 ≡ 𝐹
 𝑝 → 𝑝 ≡ 𝑇
 𝑝 → 𝑇 ≡ 𝑇
 𝑝 → 𝐹 ≡∼ 𝑝
 𝑇 → 𝑝 ≡ 𝑝
 𝐹 → 𝑝 ≡ 𝑇
 𝑝 ↔ 𝑝 ≡ 𝑇
 𝑝 ↔ 𝑇 ≡ 𝑝
 𝑝 ↔ 𝐹 ≡∼ 𝑝

2. LAWS OF ALGEBRA OF PREPOSITIONS
Mayengo,
M.
M
2
Commutative Law
 𝑝 ∨ 𝑞 ≡ 𝑞 ∨ 𝑝
 𝑝 ∧ 𝑞 ≡ 𝑞 ∧ 𝑝
 𝑝 → 𝑞 ≠ 𝑞 → 𝑝
 𝑝 ↔ 𝑞 ≡ 𝑞 ↔ 𝑝
The Law of Double
Negation
 ∼ ∼ 𝑝 ≡ 𝑝
Complement Law
 𝑝 ∨∼ 𝑝 ≡ 𝑇
 𝑝 ∧∼ 𝑝 ≡ 𝐹
 𝑝 →∼ 𝑝 ≡∼ 𝑝
 ∼ 𝑝 → 𝑝 ≡ 𝑝
 𝑝 ↔∼ 𝑝 ≡ 𝐹

3. LAWS OF ALGEBRA OF PREPOSITIONS
Mayengo,
M.
M
3
Associative Law
 𝑝 ∨ 𝑞 ∨ 𝑟 ≡ 𝑝 ∨ 𝑞 ∨ 𝑟
 𝑝 ∧ 𝑞 ∧ 𝑟 ≡ 𝑝 ∧ 𝑞 ∧ 𝑟
Distributive Law
 𝑝 ∨ 𝑞 ∧ 𝑟 ≡ 𝑝 ∨ 𝑞 ∧ (𝑝 ∨ 𝑟)
 𝑝 ∧ 𝑞 ∨ 𝑟 ≡ 𝑝 ∧ 𝑞 ∨ (𝑝 ∧ 𝑟)

4. LAWS OF ALGEBRA OF PREPOSITIONS
Mayengo,
M.
M
4
The Law of Absorption
 𝑝 ∨ 𝑝 ∧ 𝑞 ≡ 𝑝
 𝑝 ∧ 𝑝 ∨ 𝑞 ≡ 𝑝
De Morgan’s Law
 ∼ 𝑝 ∨ 𝑞 ≡∼ 𝑝 ∧∼ 𝑞
 ∼ 𝑝 ∧ 𝑞 ≡∼ 𝑝 ∨∼ 𝑞

5. LAWS OF ALGEBRA OF PREPOSITIONS
Mayengo,
M.
M
5
The Law of Equivancy of Contrapositive
 𝑝 → 𝑞 ≡∼ 𝑞 →∼ 𝑝
The Law of Syllogism
 If 𝑝 → 𝑞 and 𝑞 → 𝑟 then 𝑝 → 𝑟
Other Laws
 𝑝 → 𝑞 ≡∼ 𝑝 ∨ 𝑞
 𝑝 ↔ 𝑞 ≡ 𝑝 → 𝑞 ∧ (𝑞 → 𝑝)

6. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
6
Tautology
 A compound statement that is always true no
matter what truth values are assigned to its
component propositions is called a tautology
 Examples: Consider the following truth tables
𝒑 ∼ 𝒑 (𝒑 ∨∼ 𝒑)
𝑇 𝐹 𝑻
𝐹 𝑇 𝑻

7. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
7
Tautology
 Examples: Consider the following truth tables
𝒑 𝒒 ∼ 𝒑 𝒑 ∨ 𝒒 ∼ 𝒑 ∨ (𝒑 ∨ 𝒒)
𝑇 𝑇 𝐹 𝑇 𝑻
𝑇 𝐹 𝐹 𝑇 𝑻
𝐹 𝑇 𝑇 𝑇 𝑻
𝐹 𝐹 𝑇 𝐹 𝑻

8. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
8
Contradictions/Fallacy
 These are compound statements which are always
false no matter what truth values are assigned to
the component propositions
 Examples: Consider the following truth tables
𝒑 ∼ 𝒑 (𝒑 ∧∼ 𝒑)
𝑇 𝐹 𝑭
𝐹 𝑇 𝑭

9. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
9
Contradictions
 Examples: Consider the following truth tables
𝒑 𝒒 𝒑 ∧ 𝒒 𝒑 ∨ 𝒒 ∼ (𝒑 ∨ 𝒒) 𝒑 ∧ 𝒒 ∧∼ (𝒑 ∨ 𝒒)
𝑇 𝑇 𝑇 𝑇 𝐹 𝑭
𝑇 𝐹 𝐹 𝑇 𝐹 𝑭
𝐹 𝑇 𝐹 𝑇 𝐹 𝑭
𝐹 𝐹 𝐹 𝐹 𝑇 𝑭

10. TAUTOLOGIES AND CONTRADICTIONS
Contingency
 These are compound statements which are neither
false nor true no matter what truth values are
assigned to the component propositions
Mayengo,
M.
M

11. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
11
Logical Equivalence
 Two or more propositions are said to be logically equivalent
(or equal) if they have the same/identical truth values.
 Logical equivalence is denoted by symbol " = "or " ≡ “
 Examples: Consider the truth values of the propositions ∼ (𝑝 ∧
𝑞) and ∼ 𝑝 ∨∼ 𝑞 bellow.
𝒑 𝒒 ∼ 𝒑 ∼ 𝒒 𝒑 ∧ 𝒒 ∼ (𝒑 ∧ 𝒒) ∼ 𝒑 ∨∼ 𝒒
𝑇 𝑇 𝐹 𝐹 𝑇 𝑭 𝑭
𝑇 𝐹 𝐹 𝑇 𝐹 𝑻 𝑻
𝐹 𝑇 𝑇 𝐹 𝐹 𝑻 𝑻
𝐹 𝐹 𝑇 𝑇 𝐹 𝑻 𝑻

12. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
12
Logical Equivalence
 The propositions ∼ (𝑝 ∧ 𝑞) and ∼ 𝑝 ∨∼ 𝑞 bellow have the
same truth values for all possible ways of assigning truth
values to the component propositions 𝑝 and 𝑞.
 Hence, we conclude that ∼ 𝑝 ∧ 𝑞 =∼ 𝑝 ∨∼ 𝑞
𝒑 𝒒 ∼ 𝒑 ∼ 𝒒 𝒑 ∧ 𝒒 ∼ (𝒑 ∧ 𝒒) ∼ 𝒑 ∨∼ 𝒒
𝑇 𝑇 𝐹 𝐹 𝑇 𝑭 𝑭
𝑇 𝐹 𝐹 𝑇 𝐹 𝑻 𝑻
𝐹 𝑇 𝑇 𝐹 𝐹 𝑻 𝑻
𝐹 𝐹 𝑇 𝑇 𝐹 𝑻 𝑻

13. TAUTOLOGIES AND CONTRADICTIONS
Mayengo,
M.
M
13
Logical Equivalence
 Similarly, we can show that 𝑝 → 𝑞 =∼ 𝑝 ∨ 𝑞.
 The truth table bellow proves the equivalence of the two
compound statements.
𝒑 𝒒 ∼ 𝒑 𝒑 → 𝒒 ∼ 𝒑 ∨ 𝒒
𝑇 𝑇 𝐹 𝑻 𝑻
𝑇 𝐹 𝐹 𝑭 𝑭
𝐹 𝑇 𝑇 𝑻 𝑻
𝐹 𝐹 𝑇 𝑻 𝑻

14. QUESTIONS
 By using truth table and laws of proposition logic,
classify the following mathematic logic formula
whether they are tautology, contradiction or
contingency statements.
 (i)(∼p→(p→q)
 (ii) (p→q)(q→p)
 (iii) p(p→q)
 (iv) (pq)→(rp)
 (v) (pq)(∼pr)
Mayengo,
M.
M