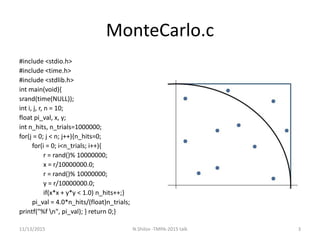
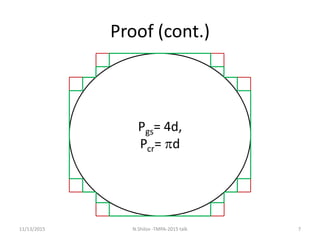
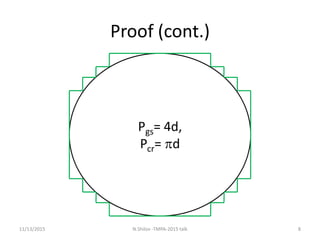
This document discusses the need to formally specify and verify standard mathematical functions in programming languages like C. It uses examples of computing pi using Monte Carlo simulation and solving quadratic equations to show that functions like rand() and sqrt() are not precisely defined, which causes problems for formal verification. The document argues that alternative functions or interval analysis approaches could provide more rigorous specifications of functions like sqrt.

1. A Need To Specify and Verify
Standard Functions
Nikolay Shilov
A.P. Ershov Institute of Informatics
Systems (Novosibirsk, Russia)

2. =4 BACAUSE OF RAND()
Part 1
11/13/2015 2N.Shilov -TMPA-2015 talk

3. MonteCarlo.c
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
int main(void){
srand(time(NULL));
int i, j, r, n = 10;
float pi_val, x, y;
int n_hits, n_trials=1000000;
for(j = 0; j < n; j++){n_hits=0;
for(i = 0; i<n_trials; i++){
r = rand()% 10000000;
x = r/10000000.0;
r = rand()% 10000000;
y = r/10000000.0;
if(x*x + y*y < 1.0) n_hits++;}
pi_val = 4.0*n_hits/(float)n_trials;
printf("%f n", pi_val); } return 0;}
11/13/2015 3N.Shilov -TMPA-2015 talk

4. Experiment
11/13/2015 4N.Shilov -TMPA-2015 talk

5. Proof
Psq= 4d,
Pcr= d
11/13/2015 5N.Shilov -TMPA-2015 talk

6. Proof (cont.)
Prs= 4d,
Pcr= d
11/13/2015 6N.Shilov -TMPA-2015 talk

7. Proof (cont.)
Pgs= 4d,
Pcr= d
11/13/2015 7N.Shilov -TMPA-2015 talk

8. Proof (cont.)
Pgs= 4d,
Pcr= d
11/13/2015 8N.Shilov -TMPA-2015 talk

9. Proof (cont.)
• The figure around the circle converges to the
circle; hence its perimeter converges to d.
• but the value of the perimeter is constant 4d;
• hence =4.
11/13/2015 9N.Shilov -TMPA-2015 talk

10. Formal Methods as a Rescue
• Let us specify the program in Hoare style by
pre- and post-conditions. The pre-condition
may be TRUE since the program has no input.
• The post-condition may be pi_val==4.0, but
since the real program works with floating
point values, it makes sense relax the post-
condition a little bit.
• Due to the exercise we may hope that
╞[TRUE] PiMC [3.9<=pi_val<=4.1].
11/13/2015 10N.Shilov -TMPA-2015 talk

11. Formal Methods as a Rescue
• But if we try to apply Floyd-Hoare methodic to
generate verification conditions and prove the
assertion then we encounter a problem of
formal semantics of the function rand() in
the assignment
r = rand()% 10000000;
that has 2 instances in the program.
11/13/2015 11N.Shilov -TMPA-2015 talk

12. Formal Methods as a Rescue
• The standard rule to generate verification
condition for assignment reads
(x)(t)
;
[(x)] x=t [(x)]
• for function rand()it leads to
(x)(rand())
.
[(x)] x=rand() [(x)]
11/13/2015 12N.Shilov -TMPA-2015 talk

13. What is rand()?!
(C reference. Rand. http://en.cppreference.com/w/c/numeric/random/rand.)
Parameters
(none)
Return value
Pseudo-random integral value between ​0​ and RAND_MAX,
inclusive.
Notes
There are no guarantees as to the quality of the random
sequence produced. …
POSIX requires that the period of the pseudo-random number
generator used by rand is at least 232
POSIX offered a thread-safe version of rand called rand_r, which
is obsolete in favor of the drand48 family of functions.
11/13/2015 13N.Shilov -TMPA-2015 talk

14. WHAT IS SQRT?
Part II
11/13/2015 14N.Shilov -TMPA-2015 talk

15. Solving Quadratic Equations
• A very popular
approach to teach
standard
input/output,
floating point type,
etc., is a program
“solving” quadratic
equation
ax2 + bx + c = 0.
#include <stdio.h>
#include <math.h>
int main(void){
float a, b, c, d, x;
printf("Input
coefficients a, b and c
and type 'enter' after
each:");
scanf("%f%f%f",&a,&b,&c);
d=b*b -4*a*c;
if (d<0) printf("No
root(s).");
else {x= (-b +
sqrt(d))/(2*a);
printf("A root is
%f.", x);} return 0;}
11/13/2015 15N.Shilov -TMPA-2015 talk

16. Solving Quadratic Equations
• We put “solving” to quotation marks because
non of conventional computers can find root
of a simple equation
x2 – 2 = 0
due to irrational nature of the number but
finite size all numeric data types in every
implementation of C.
11/13/2015 16N.Shilov -TMPA-2015 talk

17. Specification says …
(C refernce. Sqrt, sqrtf, sqrtl.
http://en.cppreference.com/w/c/numeric/math/sqrt. )
sqrt, sqrtf, sqrtl
C Numerics Common mathematical functions
Defined in header <math.h>
…
Parameters
arg - floating point value
Return value
If no errors occur, square root of arg , is returned.
11/13/2015 17N.Shilov -TMPA-2015 talk

18. Alternatives for sqrt
• It makes sense to introduce another function
with two arguments SQR(Y, E) where Y stays for
the argument and E stays for accuracy, that can
be formally specified by the following clauses:
• If Y0 then let A0 be square root of Y, i.e. Y=A2.
• if E>0 then SQR(Y, E) must return a floating value
X 0 that differs from A less than E, i.e.
|X-A|<E.
11/13/2015 18N.Shilov -TMPA-2015 talk

19. (NOT YET A ) CONCLUSION
Part III
11/13/2015 N.Shilov -TMPA-2015 talk 19

20. (Not yet a ) Conclusion
• A need of better specification and validation
of standard functions is well-recognized by
industrial and academic professional
community as well as the problem of
conformance of their implementation with the
specification
11/13/2015 20N.Shilov -TMPA-2015 talk

21. (Not yet a ) Conclusion
• J. Harrison, Formal Verification of Square Root Algorithms. Formal
Methods in System Design, 2003, Vol.22(2), p.143-153.
• V. Kuliamin, Standardization and Testing of Mathematical Functions
Programming and Computer Software, 2007, Vol. 33 (3), p.154-173.
• V.V. Kuliamin, Standardization and Testing of Mathematical
Functions in floating point numbers. Proceedings of Int. Conf.
Perspectives of Systems Informatics PSI-2009. Lecture Notes in
Computer Science, 2010, Vol. 5947, p. 257-268.
• A.V. Promsky, C Program Verification: Verification Condition
Explanation and Standard Library. Automatic Control and Computer
Sciences, 2012, Vol. 46, No. 7, p. 394–401.
• A.V. Promsky, Experiments on self-applicability in the C-light
verification system. Bull. Nov.Comp. Center, Comp. Science, Vol.35,
2013, p.85-99.
11/13/2015 21N.Shilov -TMPA-2015 talk

22. (Not yet a ) Conclusion
• A very serious obstacle for formal verification
of standard mathematical functions is a need
of axiomatization of floating point arithmetic.
• Maybe interval analysis approach and
formalization of interval arithmetic may help
to tackle the problem for functions like sqrt
(but not for functions like rand).
11/13/2015 22N.Shilov -TMPA-2015 talk