More Related Content
PPTX
Time series analysis with python chapter2-1 PDF
PDF
PDF
PPT
PDF
Granger因果による�時系列データの因果推定(因果フェス2015) PDF
PDF
Similar to Time series analysis with python 1 3
PDF
PPTX
PDF
構造方程式モデルによる因果推論: 因果構造探索に関する最近の発展 PDF
PPTX
PDF
PPTX
PDF
PDF
PDF
Analysis of clinical trials using sas 勉強用 isseing333 PDF
連続時間フラクショナル・トピックモデル(NLP2023 金融・経済ドメインのための言語処理) PPTX
PPT
PPTX
PPTX
PDF
一般化線形モデル (GLM) & 一般化加法モデル(GAM) PDF
対応分析研究会第20回v1.0.pdf 組合せ論的枠組み、並べ替え検定(リサンプリング)の整理 PDF
PDF
20101002 cd sigfin_spx_ss PPTX
Time series analysis with python 1 3
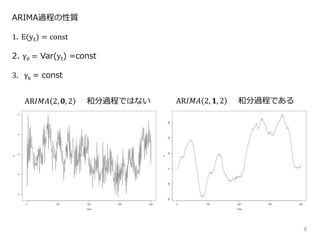
- 1.
- 2.
- 3.
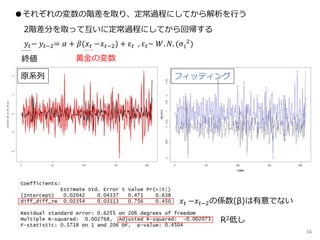
- 4.
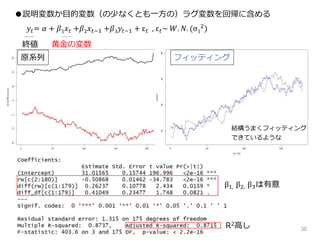
- 5.
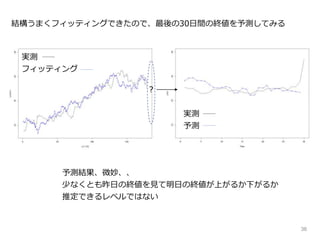
- 6.
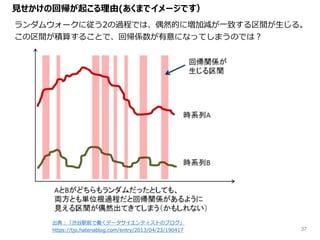
- 7.
- 8.
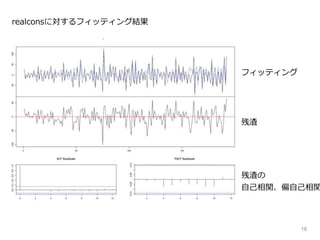
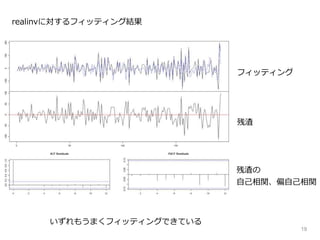
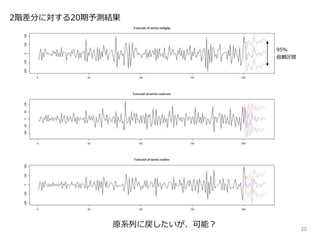
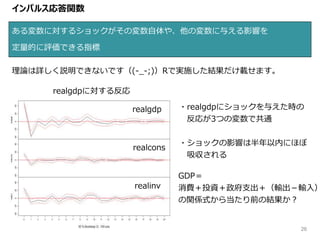
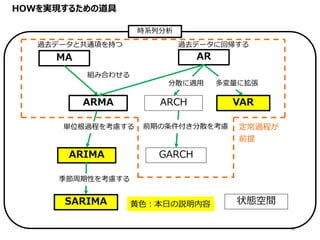
8
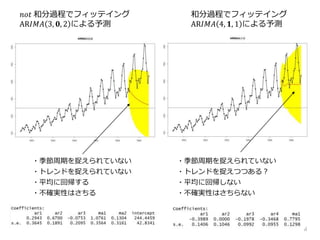
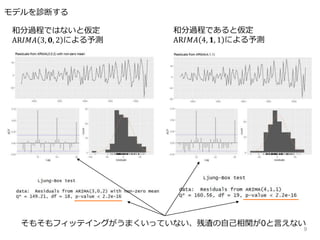
𝑛𝑜𝑡 和分過程でフィッテイング
AR𝐼𝑀𝐴 3,𝟎, 2 による予測
・季節周期を捉えられていない
・トレンドを捉えられていない
・平均に回帰する
・不確実性はさちる
和分過程でフィッテイング
AR𝐼𝑀𝐴 4, 𝟏, 1 による予測
・季節周期を捉えられていない
・トレンドを捉えつつある?
・平均に回帰しない
・不確実性はさちらない
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
1. y1t を用いてOLSでフィッティングし、残渣平方和(SSR1)を計算
2.以下の制約を課したモデルで同様に、残渣平方和(SSR0)を計算
𝑦1𝑡 ‘= 𝑐1 + φ11,1 𝑦1,𝑡−1 + φ11,2 𝑦1,𝑡−2 + ε1𝑡
3. F統計量を計算する
4.rFをカイ二乗分布表のχ2
0.05(r)の値と比較
rF > χ2
0.05(r) → 𝑦2 から 𝑦1
へのグレンジャー因果が存在する
rF < χ2
0.05(r) → 𝑦2 から 𝑦1
へのグレンジャー因果は存在しない 23
2変量のVAR 2 モデルに当てはめて考える
𝑦1𝑡 = 𝑐1 + φ11,1 𝑦1,𝑡−1 + φ12,1 𝑦2,𝑡−1 + φ11,2 𝑦1,𝑡−2 + φ12,2 𝑦2,𝑡−2 + ε1𝑡
𝑦2𝑡 = 𝑐1 + φ21,1 𝑦1,𝑡−1 + φ22,1 𝑦2,𝑡−1 + φ21,2 𝑦1,𝑡−2 + φ22,2 𝑦2,𝑡−2 + ε2𝑡
𝑦1𝑡 : 本日のアメリカの株価 、 𝑦1,𝑡−1 :昨日のアメリカの株価 、𝑦1,𝑡−2 :一昨日のアメリカの株価
𝑦2𝑡 : 本日の日本の株価 、 𝑦2,𝑡−1 :昨日の日本の株価 、𝑦2,𝑡−2 :一昨日の日本の株価
r=2 (制約の数)
T=201 (標本数)
n=2 (変量数)
p=2(ラグ)
- 24.
- 25.
25
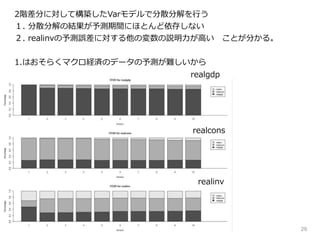
グレンジャー因果性検定を実施する
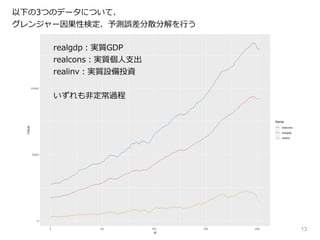
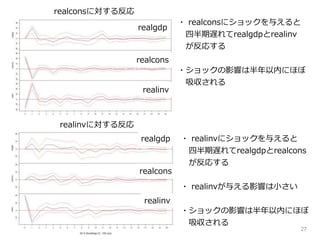
■realgdp → realcons, realinv の因果性あり
■realcons → realgdp , realinv の因果性あり
帰無仮説H0:各変数群がその他の変数に対して「グレンジャー因果性」がない
棄却
棄却
■realinv → realgdp , realcons の因果性あり
棄却
いずれの変数
も他の変数に
対して、
因果性ありという
結果になった
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.




![時系列方向の説明にARIMA(p,d,q)を用い、
周期の方向にARIMA(P,D,Q)を用いたモデル
ARIMA (p,d,q)(P,D,Q)[s] と表記
10
SARIMA過程
季節周期
原系列
季節成分
トレンド成分
残渣
乗客者数のデータを分解する](https://image.slidesharecdn.com/timeseriesanalysiswithpython-13-200506072743/85/Time-series-analysis-with-python-1-3-10-320.jpg)
![11
ARIMA(1,1,0)(0,1,0)[12]
・季節周期を捉えられている
・トレンドを捉えられている
・平均に回帰しない
・不確実性はさちらない
トレンド成分
トレンドの傾きが
増しているため追随
できていない](https://image.slidesharecdn.com/timeseriesanalysiswithpython-13-200506072743/85/Time-series-analysis-with-python-1-3-11-320.jpg)