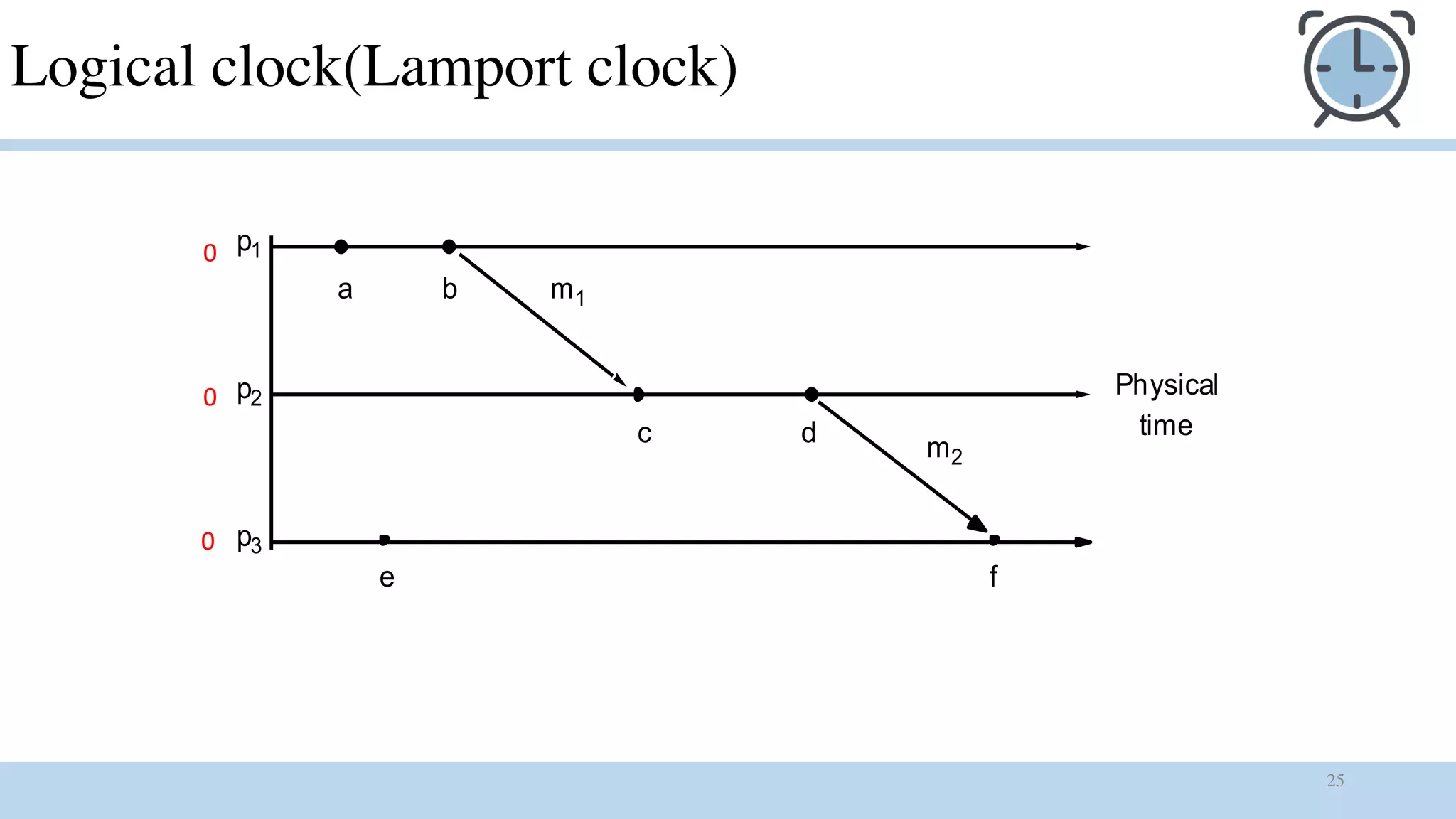
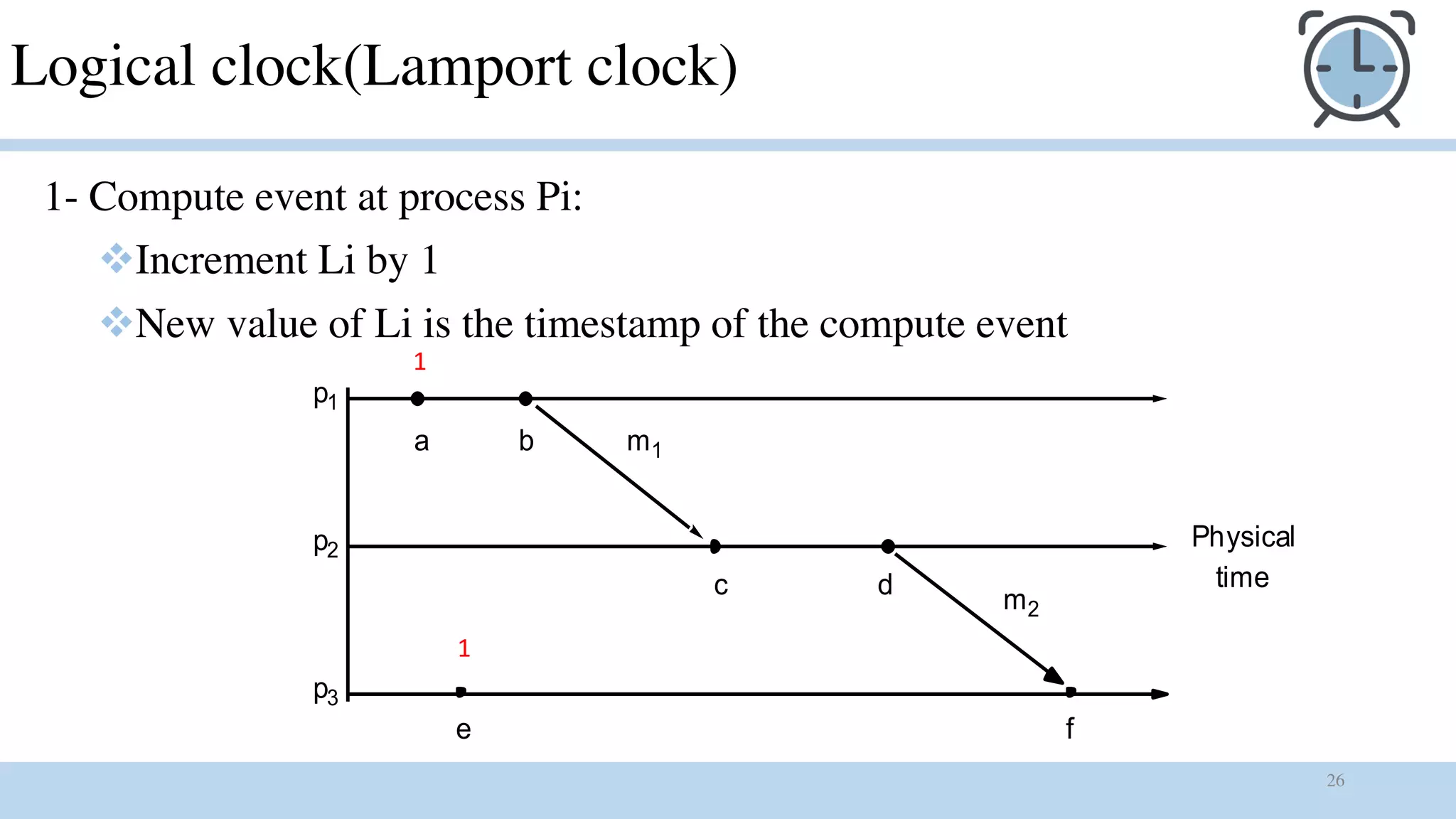
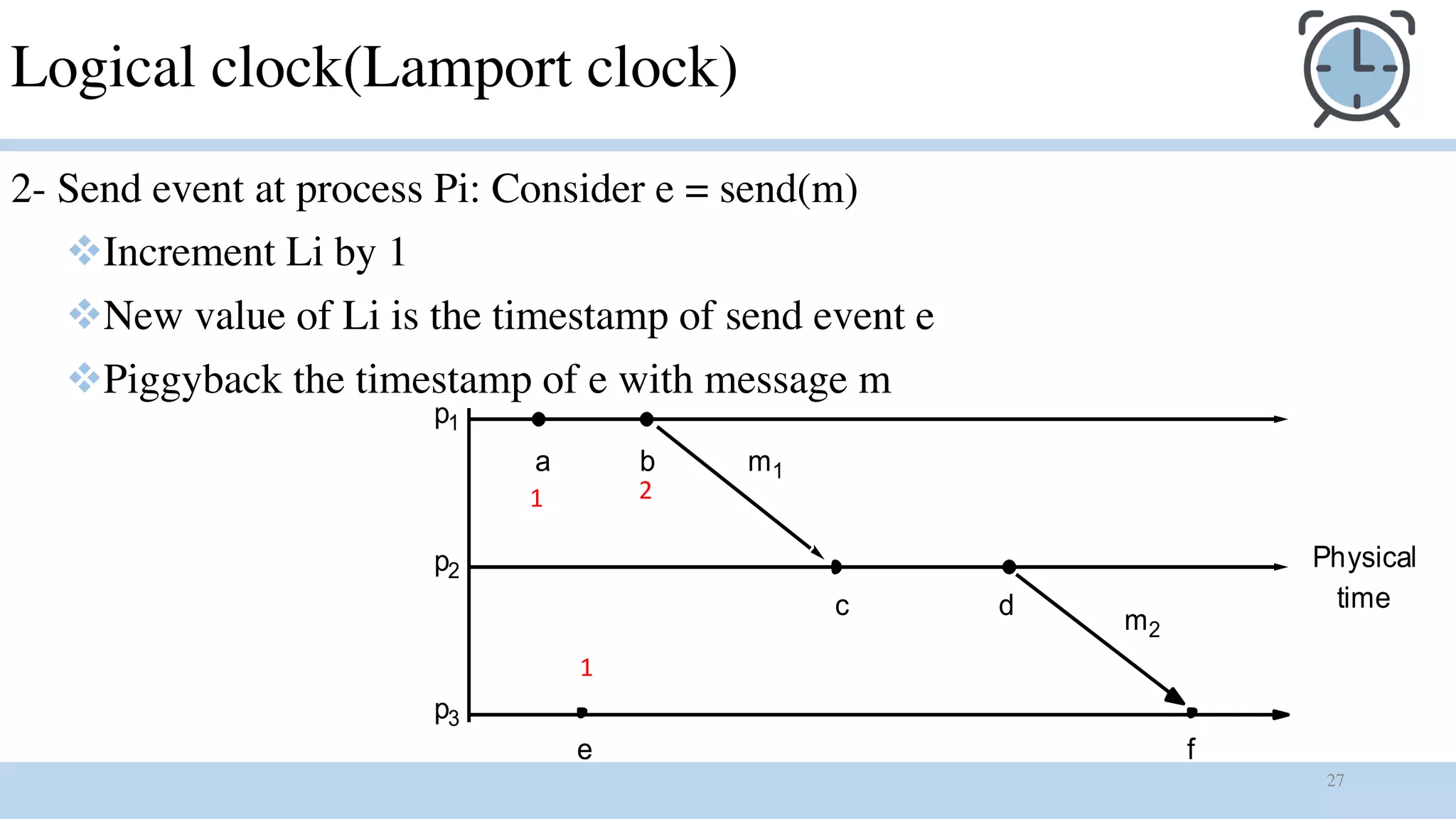
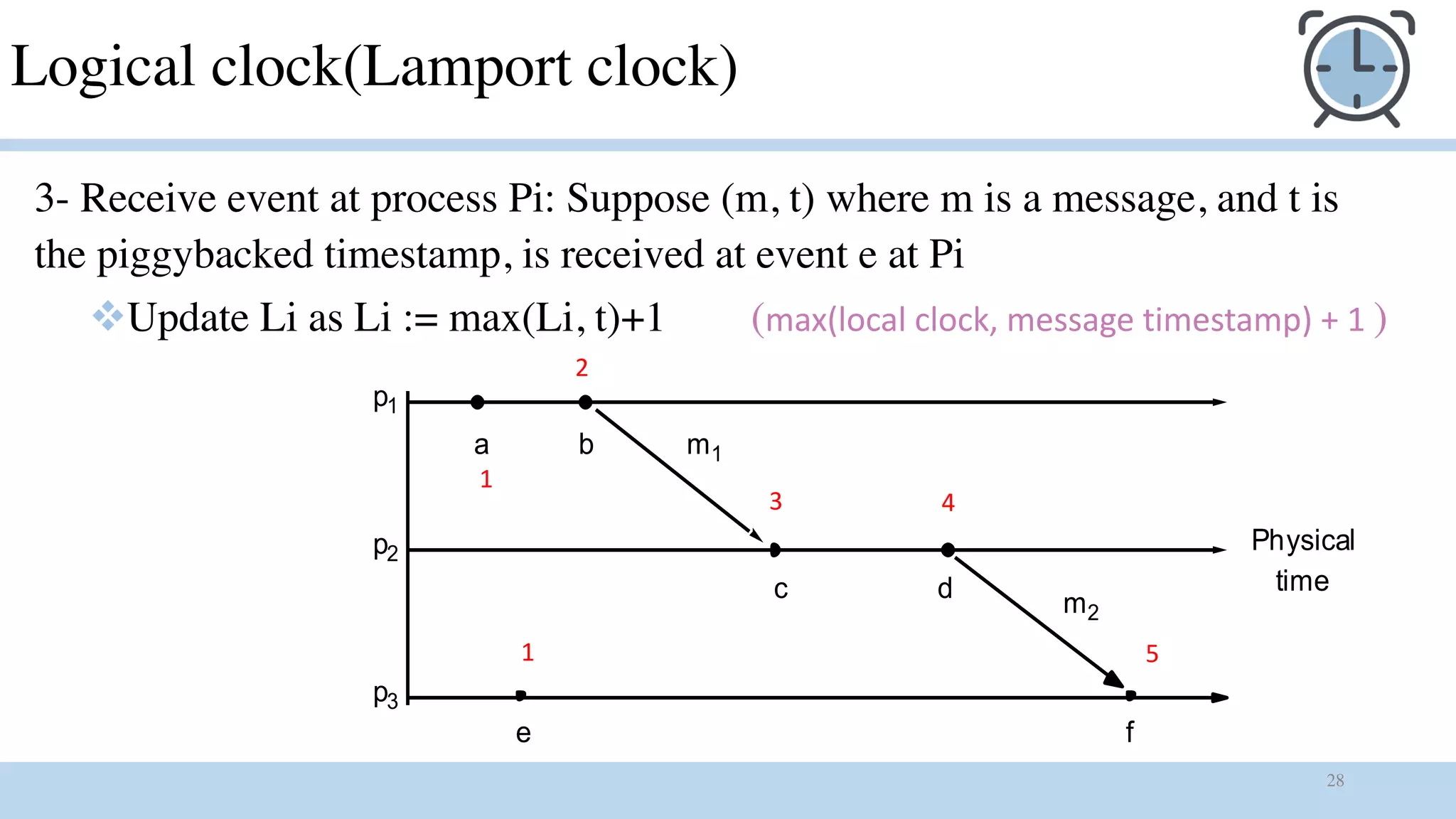
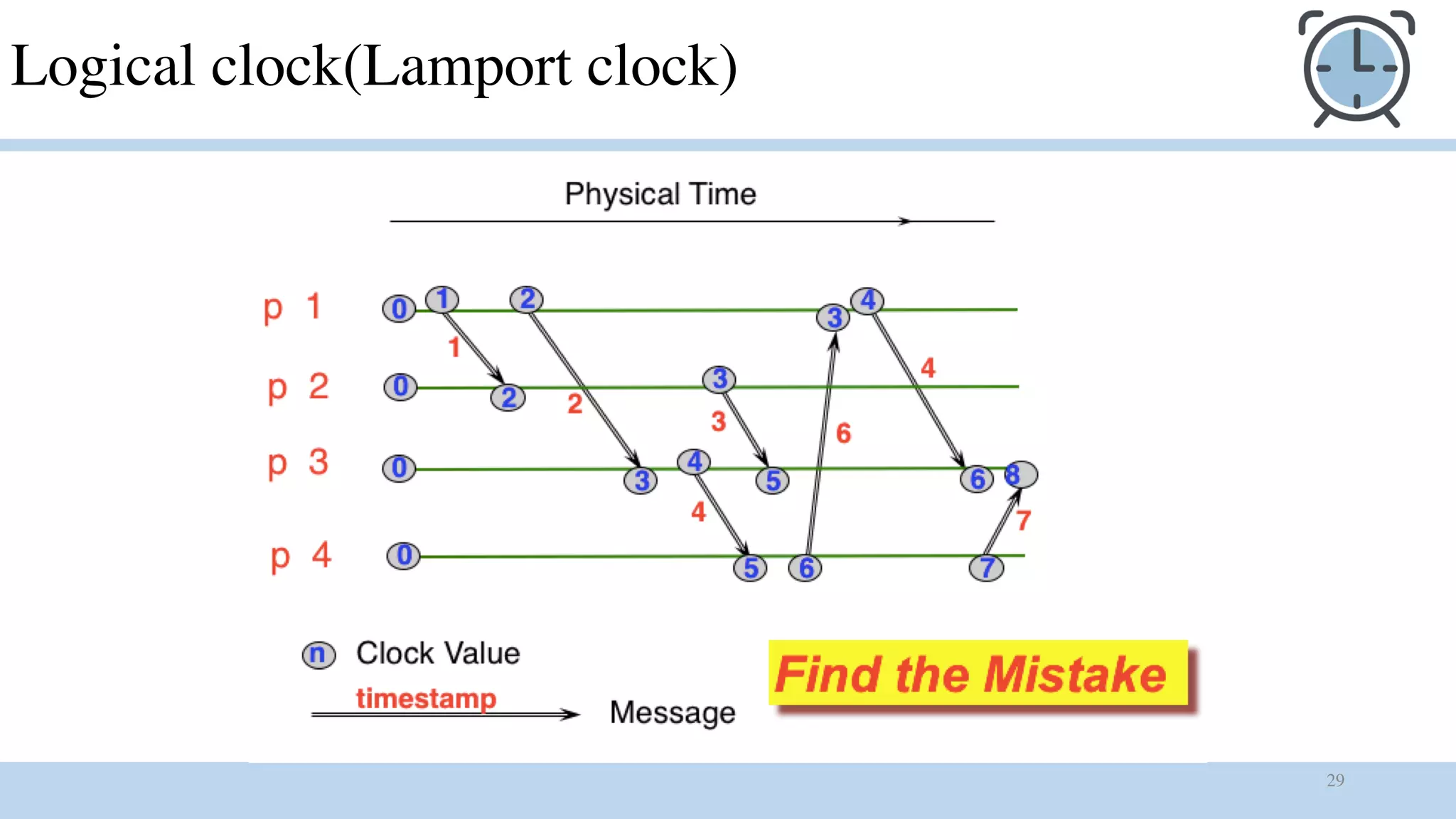
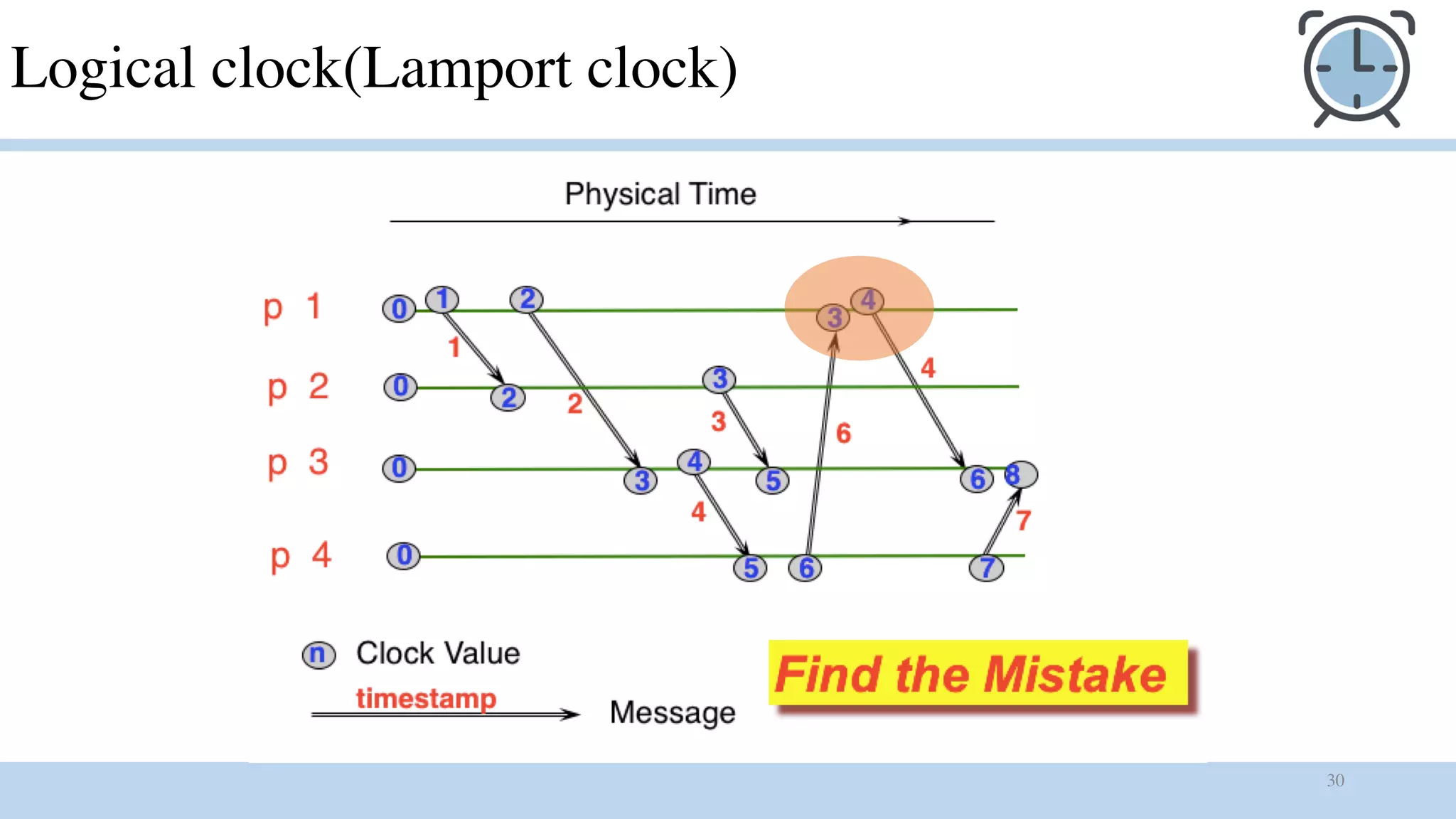
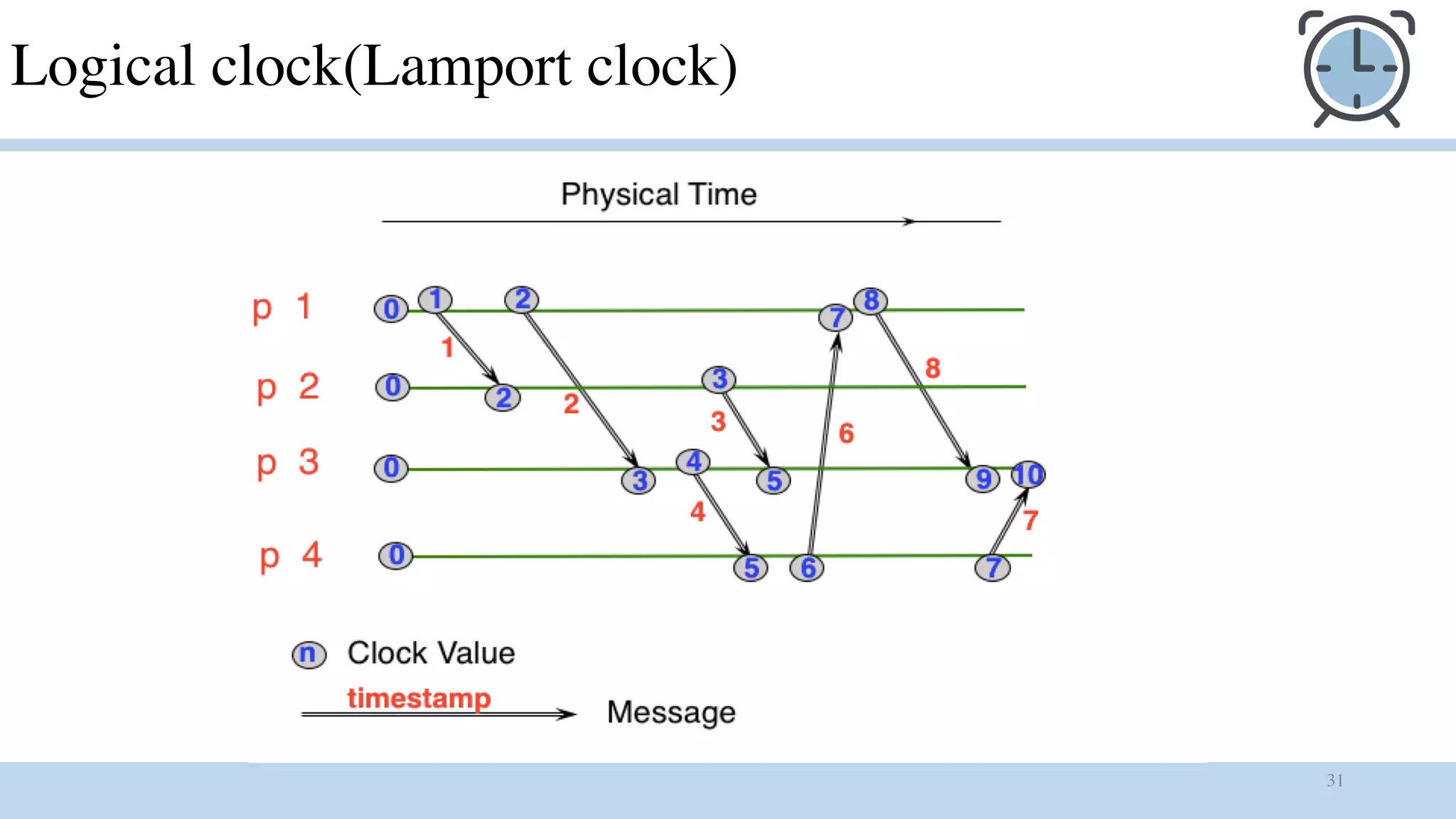
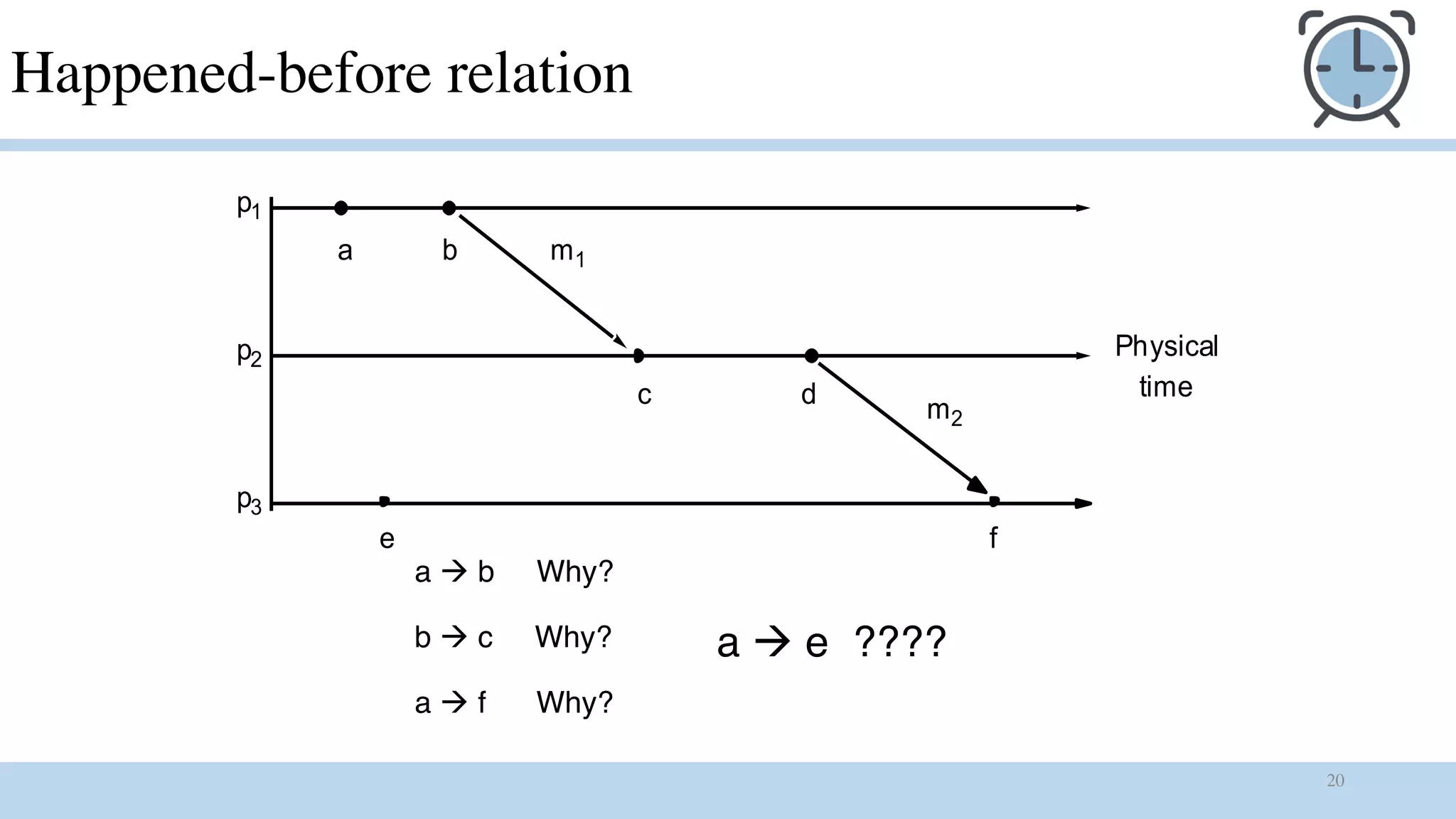
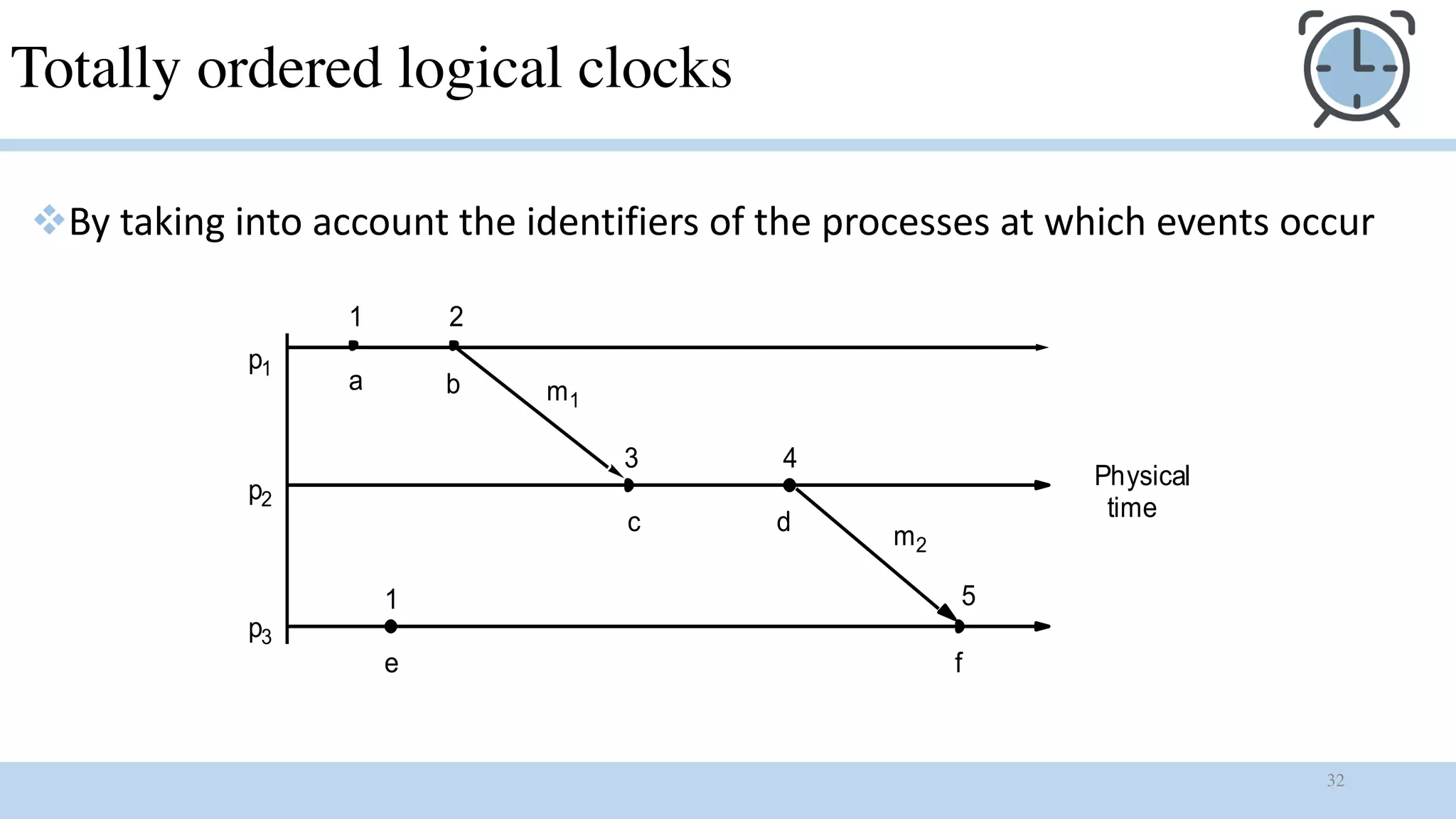
1) Logical clocks are used to provide a total ordering of events in an asynchronous distributed system where there is no global clock. Each process maintains a local logical clock that is incremented for compute and send events. The clock is updated based on timestamp values piggybacked in received messages. 2) The happened-before relation defines a partial ordering of events based on causality. Logical clocks extend this to a total ordering but the ordering is arbitrary and may not match the perceived order of users. 3) While logical clocks provide total ordering, the timestamps do not preclude concurrent events from having the same value. Vector clocks were developed to address this limitation of Lamport clocks.

1. In the name of
God
1

2. 2
Institute for Advanced Studies in Basic Sciences
Time in distributed systems
Mohammad Amid Abbasi - Asieh Hajtaghi
Teacher: Dr Z.Narimani
Spring 2018

3. 3
vIntroduction
vPartial Ordering
vTotal ordering
vConclusion
vFuture works
Contents

4. Introduction

5. 5
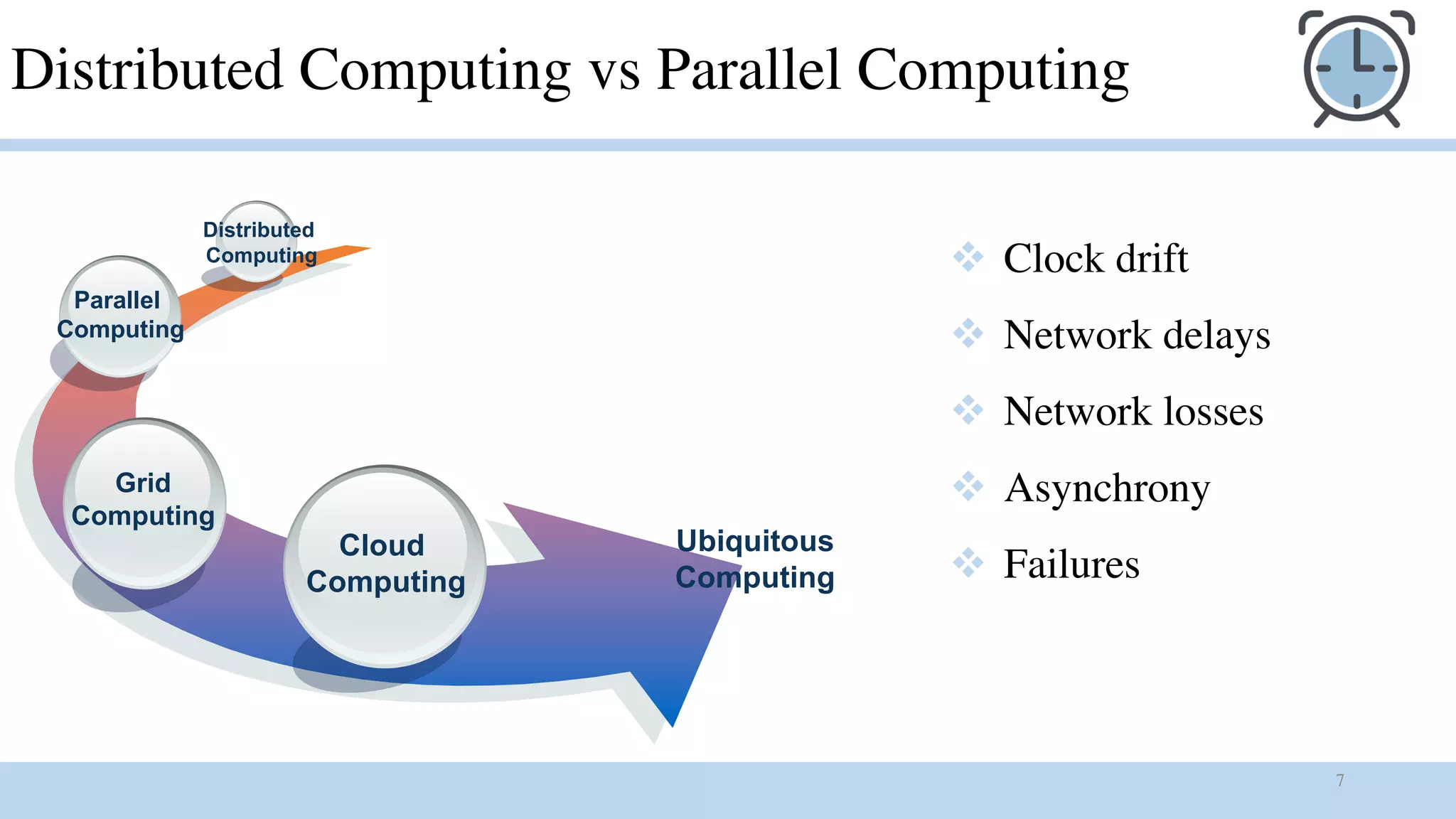
What is a Distributed System?
A distributed system is a collection of independent computers that appear to the users of
the system as a single computer.
[Andrew Tanenbaum]
A distributed system is several computers doing something together. Thus, a distributed
system has three primary characteristics: multiple computers, interconnections, and shared
state.
[Michael Schroeder]

6. 6
Why do these definitions look inadequate to us?
Because we are interested in the insides of a distributed
system
v design and implementation
v Maintenance
v Algorithmics (“protocols” or “distributed algorithms”)

7. 7
Distributed Computing vs Parallel Computing
Cloud
Computing
Grid
Computing
Parallel
Computing
Distributed
Computing
Ubiquitous
Computing
v Clock drift
v Network delays
v Network losses
v Asynchrony
v Failures

8. 8
About Time
v “Time is what keeps everything from happening at once.” Ray cummings
v The concept of time is fundamental to our way of thinking. It is derived
from the more basic concept of the order in which events occur.
v Time in a computer:
v How do computers keep track of wall clock time?
RTC and NTP
v How do operating systems know when to switch processes and otherwise schedule events?
clock interrupt
v How do applications measure the passage of time?
system calls

9. 9
Synchronization is important
v Bus caching example
v Cloud airline reservation system example
v Ordering events

10. 10
Why is it challenging?
v Physical clocks are inaccurate and we have uncertainty in network
v It is impossible to maintain a single global notion of time
v Clocks cannot be synchronized perfectly across a distributed system
v Unlike processors (CPUs) within one server which can share a system
clock

11. 11
Synchronous vs asynchronous
v Process execution speed
v Message transmission delays
v Clock drift rate
v A protocol for an asynchronous system will also work for a synchronous
system (though not vice-versa)

12. born February 7, 1941
New York
12
v Time, Clocks, and the Ordering of Events in a Distributed System
v 1978
v 10907 citation
v Communications of the ACM
About the paper

13. 13
We begin by defining our system more precisely
v An Asynchronous Distributed System consists of a number of processes
v Each process has a state (values of variables).
v State of a may change as a result of a computation step or communication
step
v An event is an abstraction to represent steps performed by a process
v Each process has a local clock, which may drift

14. 14
We begin by defining our system more precisely
v Each process has a local clock – events within a process can be assigned
timestamps, and thus ordered linearly.
v But – in a distributed system, we also need to know the time order of
events across different processes.
v Event types in a message passing system:
v Compute event
v Send event
v Receive event

15. 15
We begin by defining our system more precisely
Space-Time diagram

16. 16
Concurrent vs Parallel
Parallel
Concurrent

17. 17
Ordering of events
v We have no global clock
v Physical clocks are inaccurate
v And we need to ordering the events

18. Partial ordering

19. 19
Happened-before relation
v“happened-before” relation defined without using real-time
vNotation: a à b a happened-before b
vThree rules for message-passing systems:
v Events on the same process: Events a and b occur at the SAME process,
and a occurs before b, then a à b
v If a = Send(m) event and b = Receive(m) event then a à b
v Transitivity: if a à b and b à c then a à c
v If a à b and b à a then a and b are (logically) concurrent events
v Concurrent events are not causally related

20. 20
Happened-before relation
p1
p2
p3
a b
c d
e f
m1
m2
Physical
time
a à b Why?
b à c Why?
a à f Why?
a à e ????

21. Total ordering

22. 22
Logical clock(Lamport clock)
v Relation before Creates a partial order among events
v Used in almost all distributed systems since then
v Almost all cloud computing systems use some form of logical ordering of
events
v Goal: Assign logical (Lamport) timestamp to each event (ordering the
events totally)

23. 23
Logical clock(Lamport clock)
vEach process Pi maintains a logical clock Li(a local counter which is an
integer)
vIntialialize Li = 0 at the start of the process
vWe will describe how timestamps are updated for each type of event
separately

24. 24
Logical clock(Lamport clock)
vEach process Pi maintains a logical clock Li(a local counter which is an
integer)
vIntialialize Li = 0 at the start of the process
vWe will describe how timestamps are updated for each type of event
separately

25. 25
Logical clock(Lamport clock)
p1
p2
p3
a b
c d
e f
m1
m2
Physical
time
0
0
0

26. 26
Logical clock(Lamport clock)
1- Compute event at process Pi:
vIncrement Li by 1
vNew value of Li is the timestamp of the compute event
p1
p2
p3
a b
c d
e f
m1
m2
Physical
time
1
1

27. 27
Logical clock(Lamport clock)
2- Send event at process Pi: Consider e = send(m)
vIncrement Li by 1
vNew value of Li is the timestamp of send event e
vPiggyback the timestamp of e with message m
p1
p2
p3
a b
c d
e f
m1
m2
Physical
time
21
1

28. 28
Logical clock(Lamport clock)
p1
p2
p3
a b
c d
e f
m1
m2
Physical
time
3- Receive event at process Pi: Suppose (m, t) where m is a message, and t is
the piggybacked timestamp, is received at event e at Pi
vUpdate Li as Li := max(Li, t)+1 (max(local clock, message timestamp) + 1 )
1
1
2
3 4
5

29. 29
Logical clock(Lamport clock)

30. 30
Logical clock(Lamport clock)

31. 31
Logical clock(Lamport clock)

32. 32
Totally ordered logical clocks
a b
c d
e f
m1
m2
21
3 4
51
p1
p2
p3
Physical
time
vBy taking into account the identifiers of the processes at which events occur

33. 33
Totally ordered logical clocks
v If e is an event occurring at pi with local timestamp Ti , and e’ is an event
occurring at pj with local timestamp Tj
v we define the global logical timestamps for these events to be
(Ti, i) and (Tj, j) , respectively
v And we define (Ti, i) < (Tj, j) if and only if either Ti <= Tj and i < j .
vThis ordering has no general physical significance (because process identifiers
are arbitrary), but it is sometimes useful

34. 34
Totally ordered logical clocks
v Lamport used it, for example, to order the entry of processes to a critical
section.

35. Conclusion

36. 36
Conclusion
v We have seen that the concept of "happening before" defines an invariant
partial ordering of the events in a distributed multi process system.
v We described an algorithm for extending that partial ordering to a somewhat
arbitrary total ordering.
v A future paper will show how this approach can be extended to solve any
synchronization problem.

37. 37
Conclusion
v The total ordering defined by the algorithm is some- what arbitrary. It can
produce anomalous behavior if it disagrees with the ordering perceived by the
system's users. This can be prevented by the use of properly synchronized
physical clocks. Our theorem showed how closely the clocks can be
synchronized.
v In a distributed system, it is important to realize that the order in which events
occur is only a partial ordering. We believe that this idea is useful in
understanding any multiprocess system.

38. Future works

39. 39
Problem of Lamport clock
v L(a) denotes Lamport or Logical timestamp of event a
vIf a à b then L(a) < L(b)
vHowever, L(b) > L(a) does not imply that a à b
v As long as these timestamps obey causality, that would work
vA pair of concurrent events doesn’t have a causal path from one event to
another
v Mattern [1989] and Fidge [1991] developed vector clocks to overcome the
shortcoming of Lamport’s clocks

40. 40
vhttps://dl.acm.org/citation.cfm?id=359563
vIndranil Gupta’s distributed systems slides
vNitin Vaidya’s distributed systems slides
vdistributed systems concepts and design by george coulouris jean
dollimore and tim kindberg ‘s book
Resources

41. 41
Thanks for your attention