Thermodynamic basics-4

Dr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 Consider that one mole of a perfect gas is
taken in a cylinder having perfectly
conducting walls and bottom, provided with
a piston. Let the cylinder be placed on a
source of heat at temperature T°C. If the
piston is now moved slowly outwards, the
gas expands, does some work and tends to
cool but it absorbs required amount of heat
from the source to keep it at the same
temperature. The work done during an
infinitesimal change in volume dv is given

 W= 𝑉1
𝑉2
𝑃 𝑑𝑉-----------(19)
 For a perfect gas, PV = RT or P = RT/V
 Substituting P = RT/V in the above
equation, we get,
 W= 𝑉1
𝑉2 RT
V
𝑑𝑉-----------(20)
 As temperature is constant during
isothermal expansion and R is a gas
constant
 W= RT
𝑉2 𝑑𝑉
= RT log
𝑣2
--------(21)Dr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 W= RT 𝑉1
𝑉2 𝑑𝑉
V
= 2.303 RT log10
𝑣2
𝑣1
--------(22)
 W=2.303 𝑃2 𝑉2log10
𝑣2
𝑣1
= 2.303 𝑃1 𝑉1log10
𝑣2
𝑣1
 W=2.303 RT log10
𝑃1
𝑃2
 W=2.303 𝑃2 𝑉2log10
𝑃1
𝑃2
= 2.303 𝑃1 𝑉1log10
𝑃1
𝑃2
 When a gas expands, work, V2 >V1 and W is
positive.
 When a gas compress, work, V2 <V1 and W is
negaitive.
 The isothermal expansion P1V1 to P2V2

 An insulated cylinder that contains 1 mole of an
ideal gas. When the gas expands by dV, the change in
its temperature is dT. The work done by the gas in
the expansion is dW=pdV; dQ=0, because the
cylinder is insulated. Put this condition in first law of
thermodynamics.
 0 = dU + dW ------------------- (23)
 At constant volume dU = Cv dT
 Where Cv = Moler Specific heat at constant volume.
 Therefore equation (1.11) becomes
 Cv dT + P dV = 0 ----------------- (24)
 According to perfect gas equation PV = RT

 dT =
P dV + V dP
𝑅
---------------
(24)
 Substitute the value of dT in equation (24), we get,
 Cv
P dV + V dP
𝑅
+ 𝑷𝒅𝒗 -------------- (25)
 Cv P dV + V dP + RPdv=0 -------------- (26)
 According to Mayer’s relation,
 CvV dP + Cv + R P dV=0 -------------- (27)
 (Cp – Cv) =R so Cv + R= Cp
 Substitute in above equation 27
 CvV dP + CpP dV=0 -------------- (28)

 Dividing equation 28 by Cv P V, we get,

CvV dP
Cv P V
+
CpP dV
Cv P V
=0

dP
P
+
Cp dV
Cv V
=0 but 𝛾 = Cp/Cv

dP
P
+ 𝛾
dV
V
=0 ------------------------(29)
 Integrating above equation
 logP + 𝛾 logV = constant
 PV 𝛾= constant ------------------------(30)
 This is relation between P and V during an adiabatic
change.

we know PV 𝛾= constant
 From perfect gas equation, PV = RT.
 P=
𝑅𝑇
𝑉
 Substituting in above equation

𝑅𝑇
𝑉
V 𝛾= constant
 𝑇 V 𝛾_1= constant --------------(31)
 This is relation between T and V during an adiabatic
change.

we know PV 𝛾= constant
 From perfect gas equation, PV = RT
 V=
𝑅𝑇
𝑃
 Substituting in above equation
 P(
𝑅𝑇
𝑃
) 𝛾= constant

𝑻
𝜸
𝑷 𝛾−1 ------------------------(32)
 This is relation between P and T during an adiabatic
change.

 Suppose that one mole of a gas expands adiabatically. Let
P1, V1 and T1 be the initial values of pressure, volume and
temperature of the gas and let P2, V2 and T2 be their final
values.
 𝑊 = 𝑉1
𝑉2
𝑃𝑑𝑣
 For an adiabatic change,
 PV 𝛾= K
 W= 𝑉1
𝑉2 𝐾
𝑉
𝛾 𝑑𝑣
 W=K 𝑉1
𝑉2
𝑉 𝛾−1
𝑑𝑣
 𝑊 = 𝐾
𝑉− 𝛾+1
− 𝛾+1
𝑉2
𝑉1

 𝑊 =
𝐾
1− 𝛾
𝑉2
− 𝛾+1
− 𝑉1
− 𝛾+1
 𝑊 =
𝐾
1− 𝛾
1
𝑉2
𝛾−1 −
1
𝑉1
𝛾−1
 For an adiabatic change,
 K=P1V1
𝛾=P2V2
𝛾

 𝑊 =
1
1− 𝛾
P2V2
𝛾
𝑉2
𝛾−1 −
P1V1
𝛾
𝑉1
𝛾−1
 𝑊 =
1
1− 𝛾
P2V2 − P1V1
 From perfect gas equation, P1V1 = RT1 and P2V2
= RT2
 𝑊 =
1
1− 𝛾
RT2 − RT1
 𝑊 =
R T2 −T1
1− 𝛾
𝑊 =
R T1 −T2
𝛾−1
 For adiabatic expansion, T2 < T1, hence W is
positive.
 While for adiabatic compression, T2 > T1,

 When a system is not affected in any way
when it allowed to interact with
surroundings, such system is known as an
isolated system. But in real application
usually we deal with a system that is
influenced in some way due to its
surroundings.“A system is said to be in a
state of thermodynamic equilibrium, if a
change of state cannot takes place while
the system is subjected to interaction with
its surroundings”. For the system to be
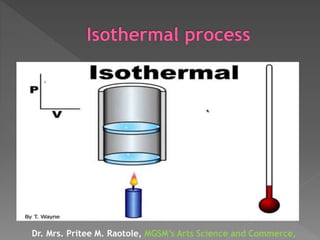
thermodynamic equilibrium it is necessaryDr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 Mechanical equilibrium- When there are no
unbalanced forces within the system and
the surrounding, then system is said to be
under mechanical equilibrium.
 Chemical equilibrium - The system is said
to be in chemical equilibrium when there
are no chemical reactions going on within
the system or there is no transfer of matter
from one part of the system to other due to
diffusion. Two systems are said to be in

 Thermal equilibrium- When the
temperature of the system is uniform and
not changing throughout the system and
also in the surroundings, then system is said
to be in thermal equilibrium. Two systems
are said to be thermal equilibrium with
each other if their temperatures are same.
 Electrical equilibrium- Electrostatic
equilibrium means that there is no net flow
of electric charge or no electric current.

 The process in which the system and
surroundings can be restored to the initial
state from the final state without producing
any changes in the thermodynamic properties
of the universe is called a reversible process.
 Let us suppose that the system has undergone
a change from state A to state B. If the system
can be restored from state B to state A, and
there is no change in the universe, then the
process is said to be a reversible process.
 The reversible process can be reversed
completely and there is no trace left to show
that the system had undergone thermodynamic
change. For the system to undergo reversible
change, it should occur infinitely slowly due toDr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 During reversible process all the changes in state
that occur in the system are in thermodynamic
equilibrium with each other. Thus there are two
important conditions for the reversible process to
occur.
 Firstly, the process should occur in infinitesimally
small steps and secondly all of the initial and final
state of the system should be in equilibrium with
each other.
 If during the reversible process the heat content
of the system remains constant, i.e. it is adiabatic
process, then the process is also isentropic
process, i.e. the entropy of the system remains
constant.

 The irreversible process is also called the
natural process because all the processes
occurring in nature are irreversible
processes.
 The natural process occurs due to the finite
gradient between the two states of the
system. For instance, heat flow between
two bodies occurs due to the temperature
gradient between the two bodies; this is in
fact the natural flow of heat.

 Similarly, water flows from high level to low
level, current flows from high potential to low
potential, etc.
 In the irreversible process the initial state of
the system and surroundings cannot be
restored from the final state.
 During the irreversible process the various
states of the system on the path of change
from initial state to final state are not in
equilibrium with each other.
 During the irreversible process the entropy of
the system increases decisively and it cannot
be reduced back to its initial value. The

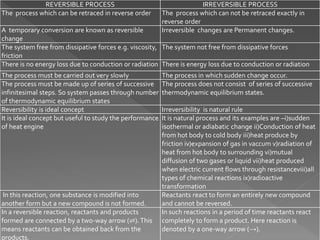
REVERSIBLE PROCESS IRREVERSIBLE PROCESS
The process which can be retraced in reverse order The process which can not be retraced exactly in
reverse order
A temporary conversion are known as reversible
change
Irreversible changes are Permanent changes.
The system free from dissipative forces e.g. viscosity,
friction
The system not free from dissipative forces
There is no energy loss due to conduction or radiation There is energy loss due to conduction or radiation
The process must be carried out very slowly The process in which sudden change occur.
The process must be made up of series of successive
infinitesimal steps. So system passes through number
of thermodynamic equilibrium states
The process does not consist of series of successive
thermodynamic equilibrium states.
Reversibility is ideal concept Irreversibility is natural rule
It is ideal concept but useful to study the performance
of heat engine
It is natural process and its examples are –i)sudden
isothermal or adiabatic change ii)Conduction of heat
from hot body to cold body iii)heat produce by
friction iv)expansion of gas in vaccum v)radiation of
heat from hot body to surrounding vi)mutual
diffusion of two gases or liquid vii)heat produced
when electric current flows through resistanceviii)all
types of chemical reactions ix)radioactive
transformation
In this reaction, one substance is modified into
another form but a new compound is not formed.
Reactants react to form an entirely new compound
and cannot be reversed.
In a reversible reaction, reactants and products
formed are connected by a two-way arrow (⇌).This
means reactants can be obtained back from the
products.
In such reactions in a period of time reactants react
completely to form a product. Here reaction is
denoted by a one-way arrow (→).

 In thermodynamics and fluid
mechanics, compressibility (also known as the
coefficient of compressibility or isothermal
compressibility) is ameasure of the relative
volume change of a fluid or solid as a response
to a pressure change. In its simple form, the
compressibility β may be expressed as;
 𝛽 = −
1
𝑉
𝜕𝑉
𝜕𝑃
 where V is volume and p is pressure. The
choice to define compressibility as
the opposite of the fraction makes
compressibility positive in the (usual) case that
an increase in pressure induces a reduction inDr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 The specification above is incomplete, because
for any object or system the magnitude of the
compressibility depends strongly on whether
the process is isentropic or isothermal.
Accordingly, isothermal compressibility is
defined:
 𝛽 𝑇 = −
1
𝑉
𝜕𝑉
𝜕𝑃
 Where the subscript T indicates that the
partial differential is to be taken at constant
temperature.
 Isentropic compressibility is defined:
 𝛽𝑆 = −
1
𝑉
𝜕𝑉
𝜕𝑃
 Where S is entropy. For a solid, the distinction
between the two is usually negligible.Dr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 The coefficient of thermal expansion describes
how the size of an object changes with a change in
temperature.
 Specifically, it measures the fractional change in
size per degree change in temperature at a
constant pressure. Several types of coefficients
have been developed: volumetric, area, and
linear.
 The choice of coefficient depends on the
particular application and which dimensions are
considered important. For solids, one might only
be concerned with the change along a length, or
over some area.
 The volumetric thermal expansion coefficient is
the most basic thermal expansion coefficient, and
the most relevant for fluids.
 In general, substances expand or contract when
their temperature changes, with expansion orDr. Mrs. Pritee M. Raotole, MGSM’s Arts Science and Commerce,

 Mathematical definitions of these coefficients
are defined below for solids, liquids, and
gases.
 In the general case of a gas, liquid, or solid,
the volumetric coefficient of thermal
expansion is given by
 𝛼 𝑉 =
1
𝑉
𝜕𝑉
𝜕𝑇
𝑃
 The subscript p indicates that the pressure is
held constant during the expansion, and the
subscript V stresses that it is the volumetric
(not linear) expansion that enters this general
definition.
 In the case of a gas, the fact that the pressure
is held constant is important, because the

Thermodynamic basics-4

More Related Content

What's hot

Similar to Thermodynamic basics-4

More from DrPriteeRaotole

Recently uploaded

Thermodynamic basics-4