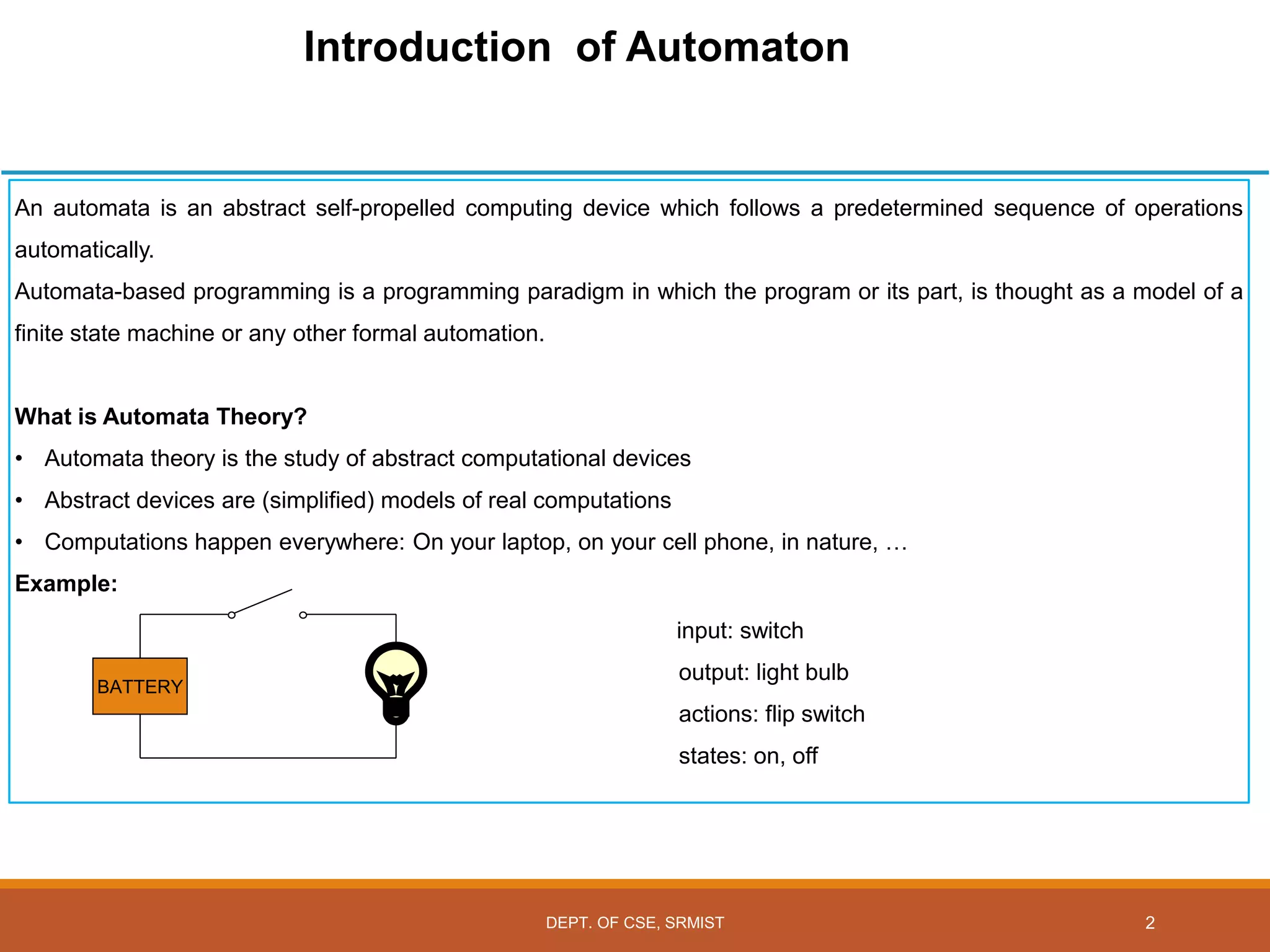
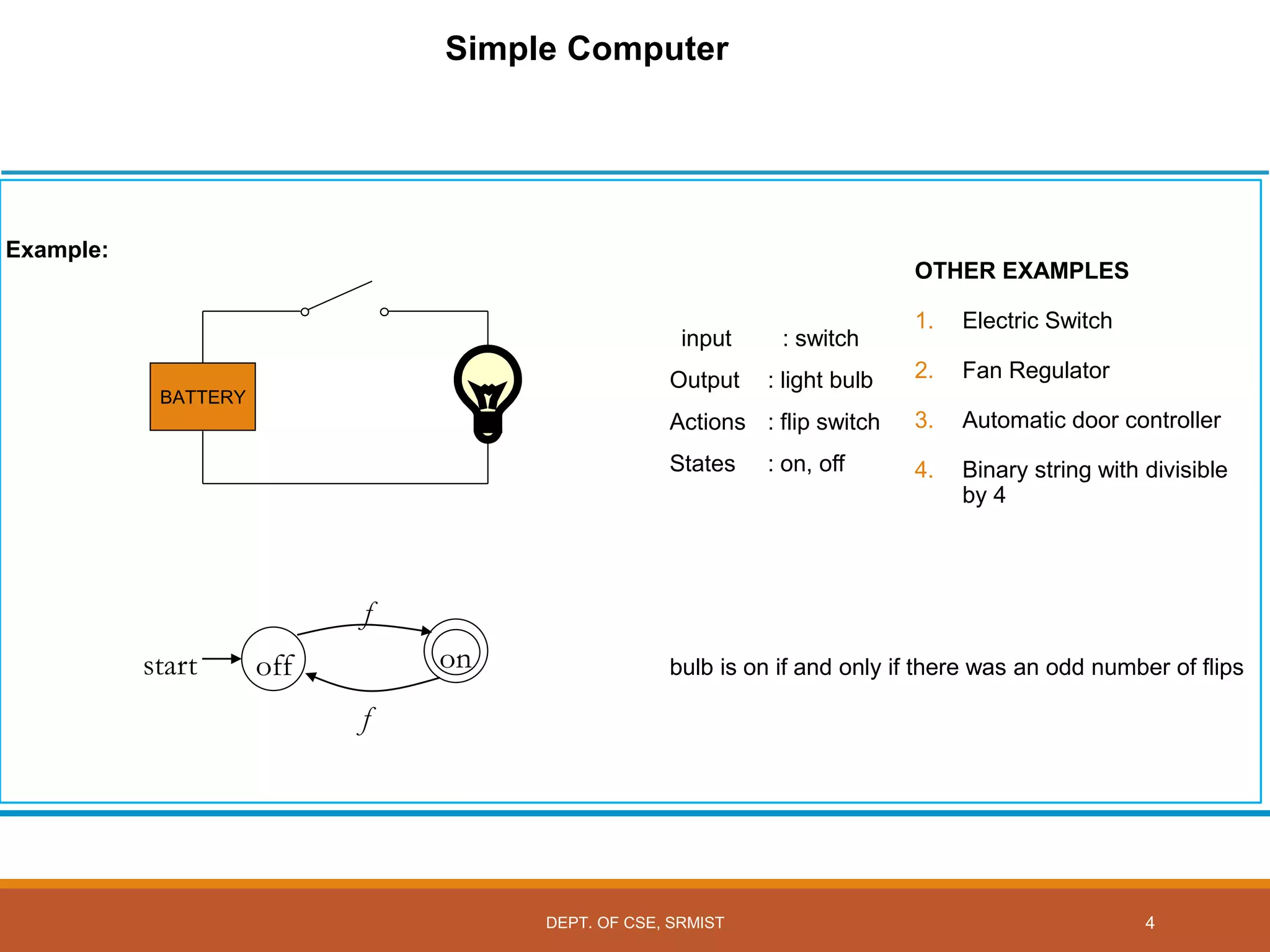
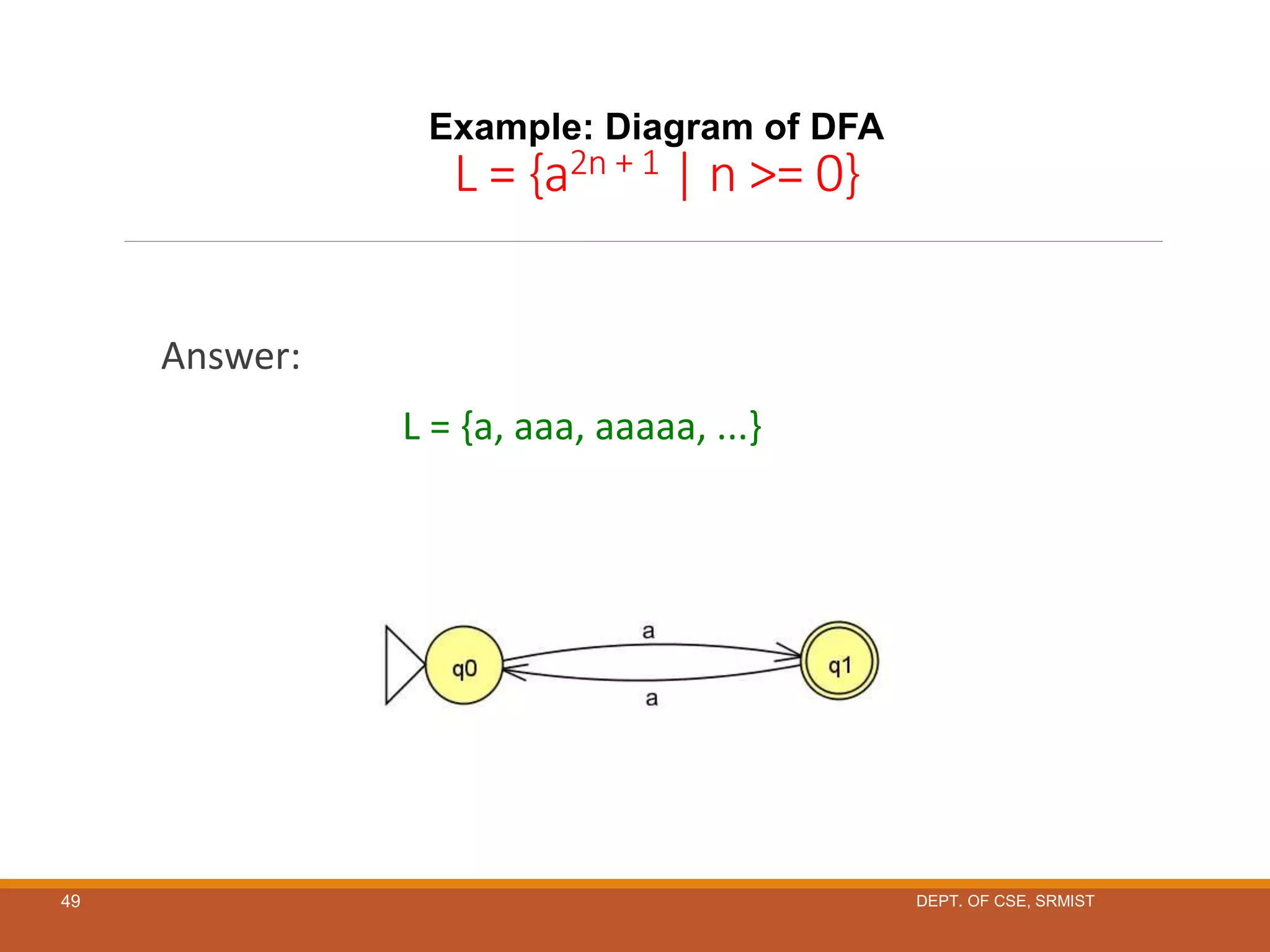
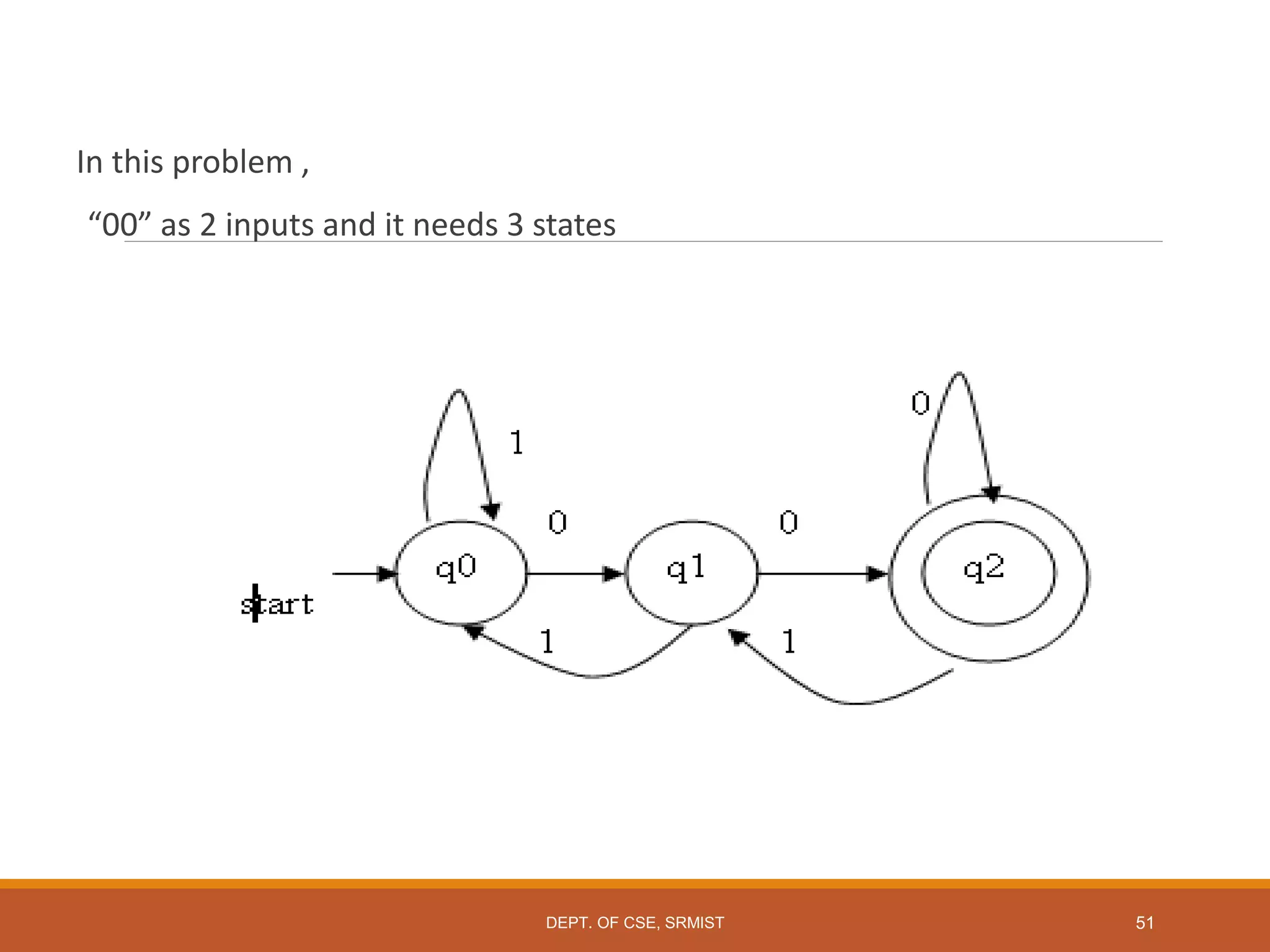
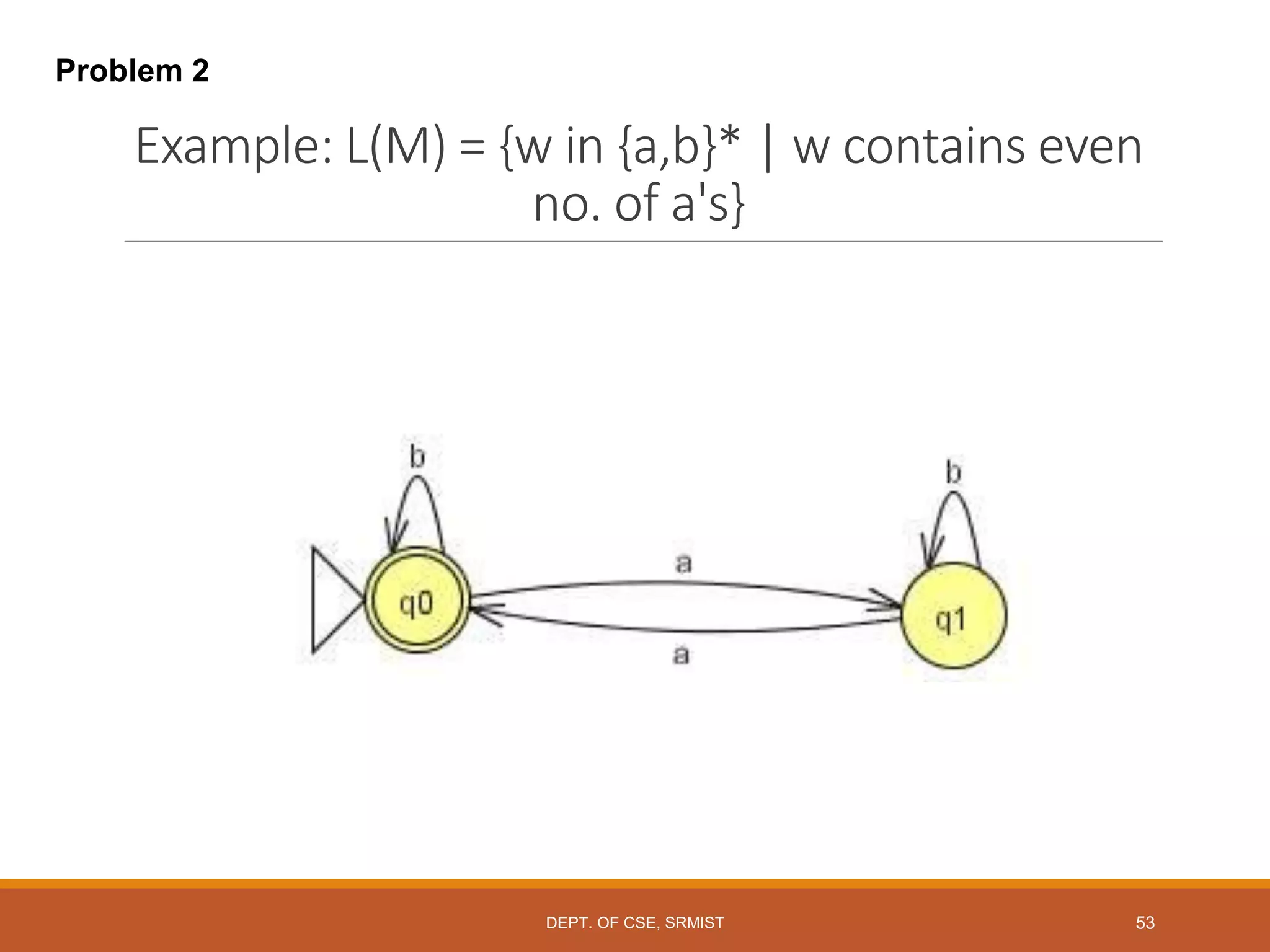
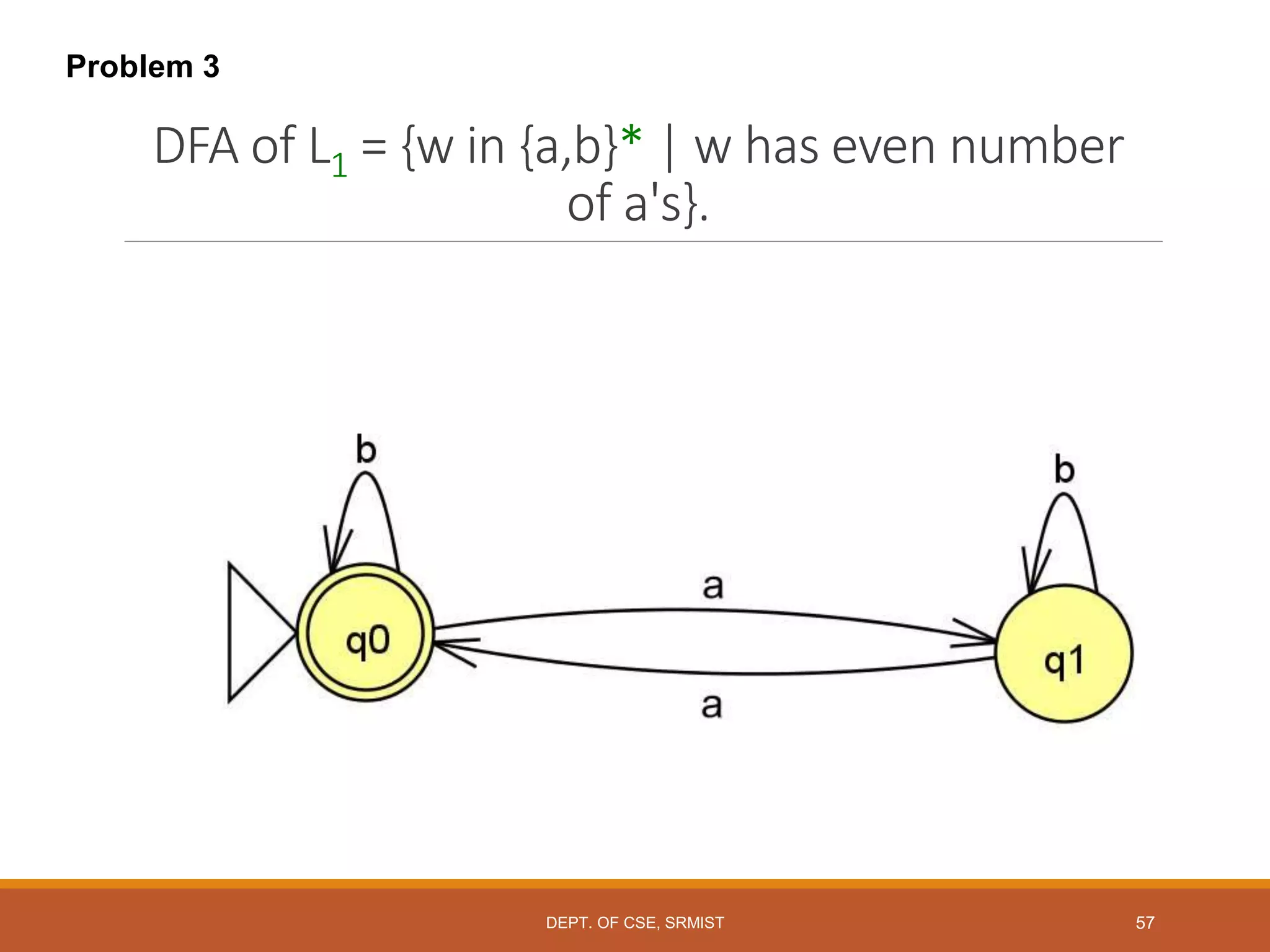
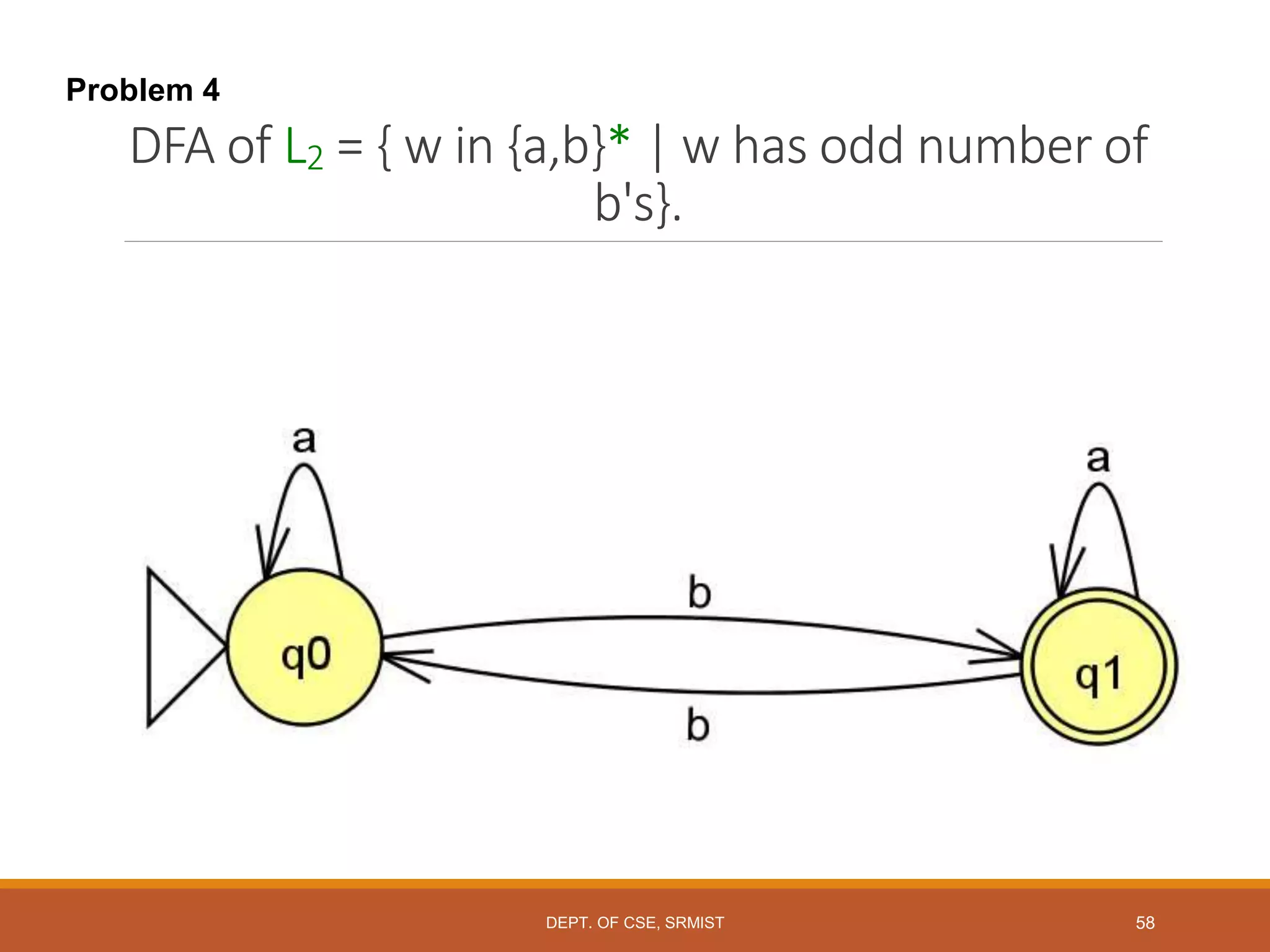
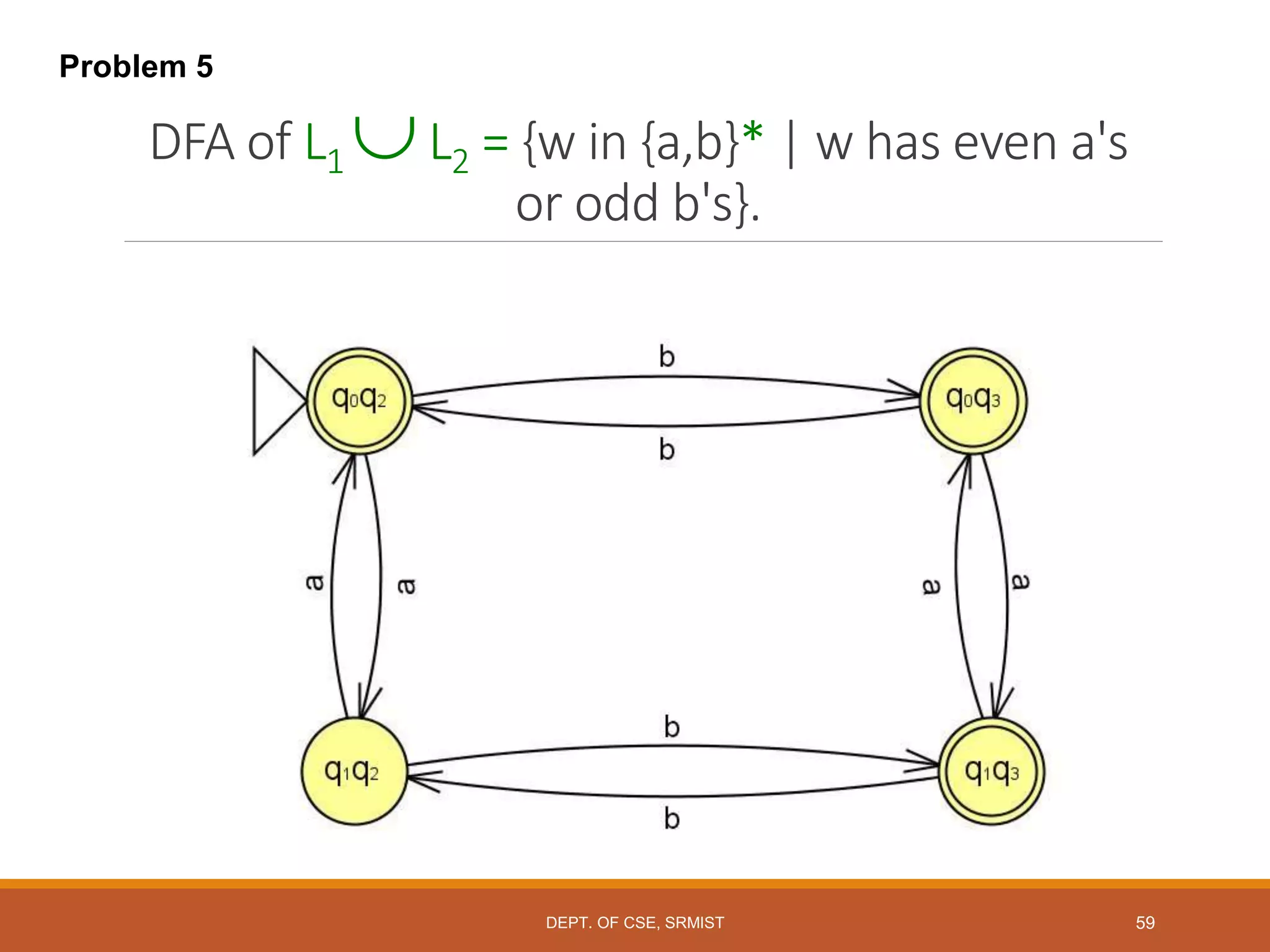
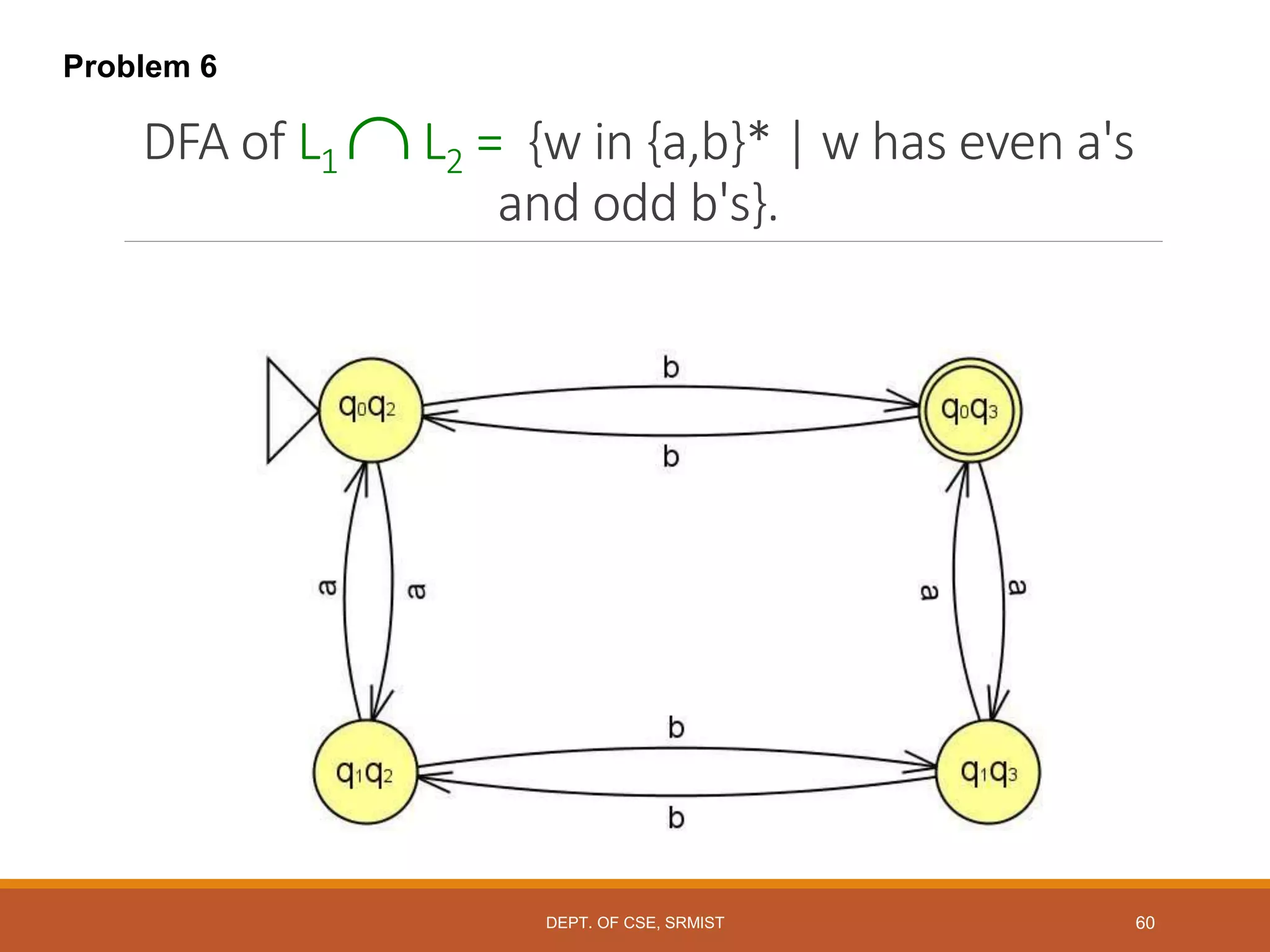
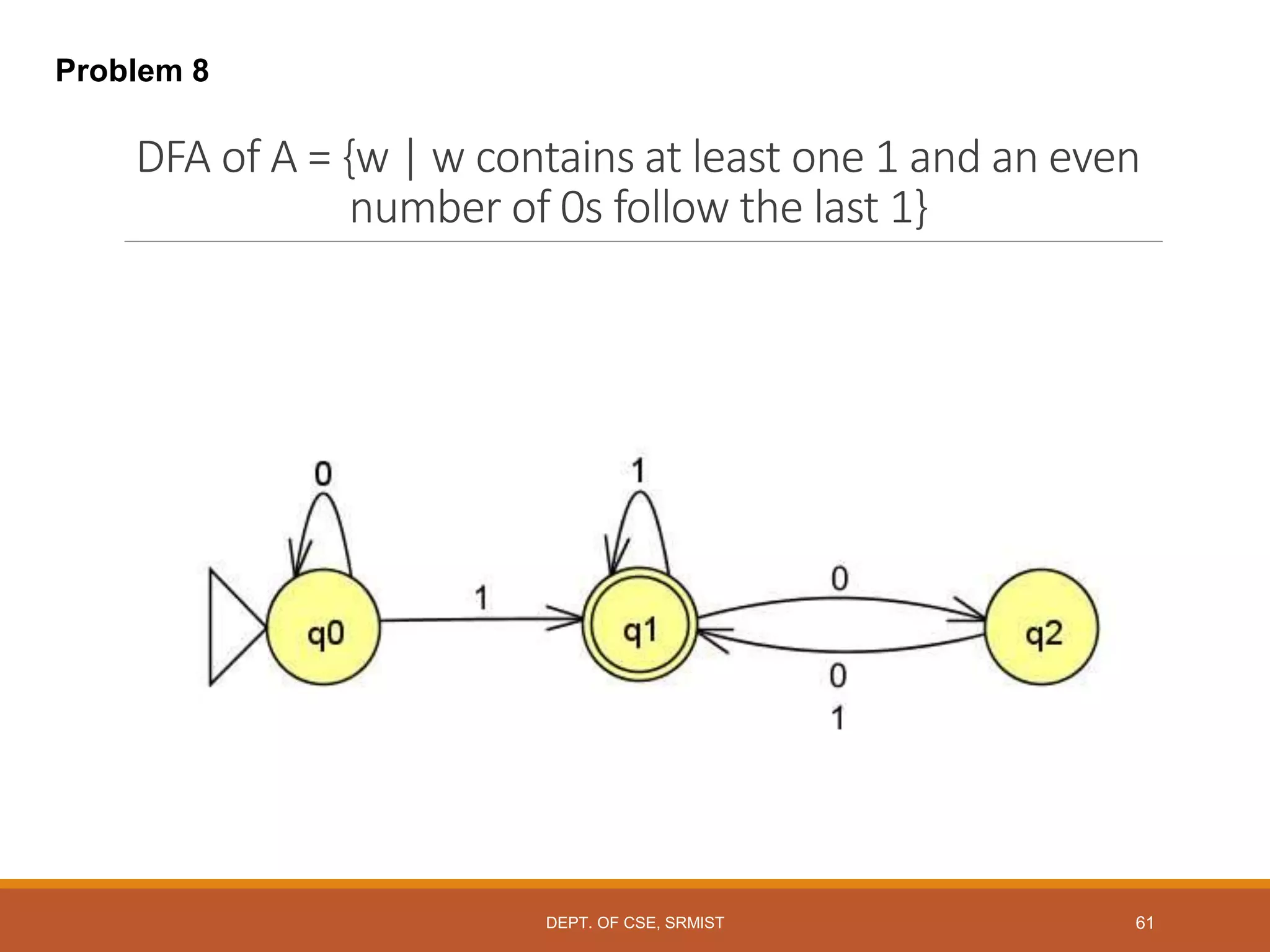
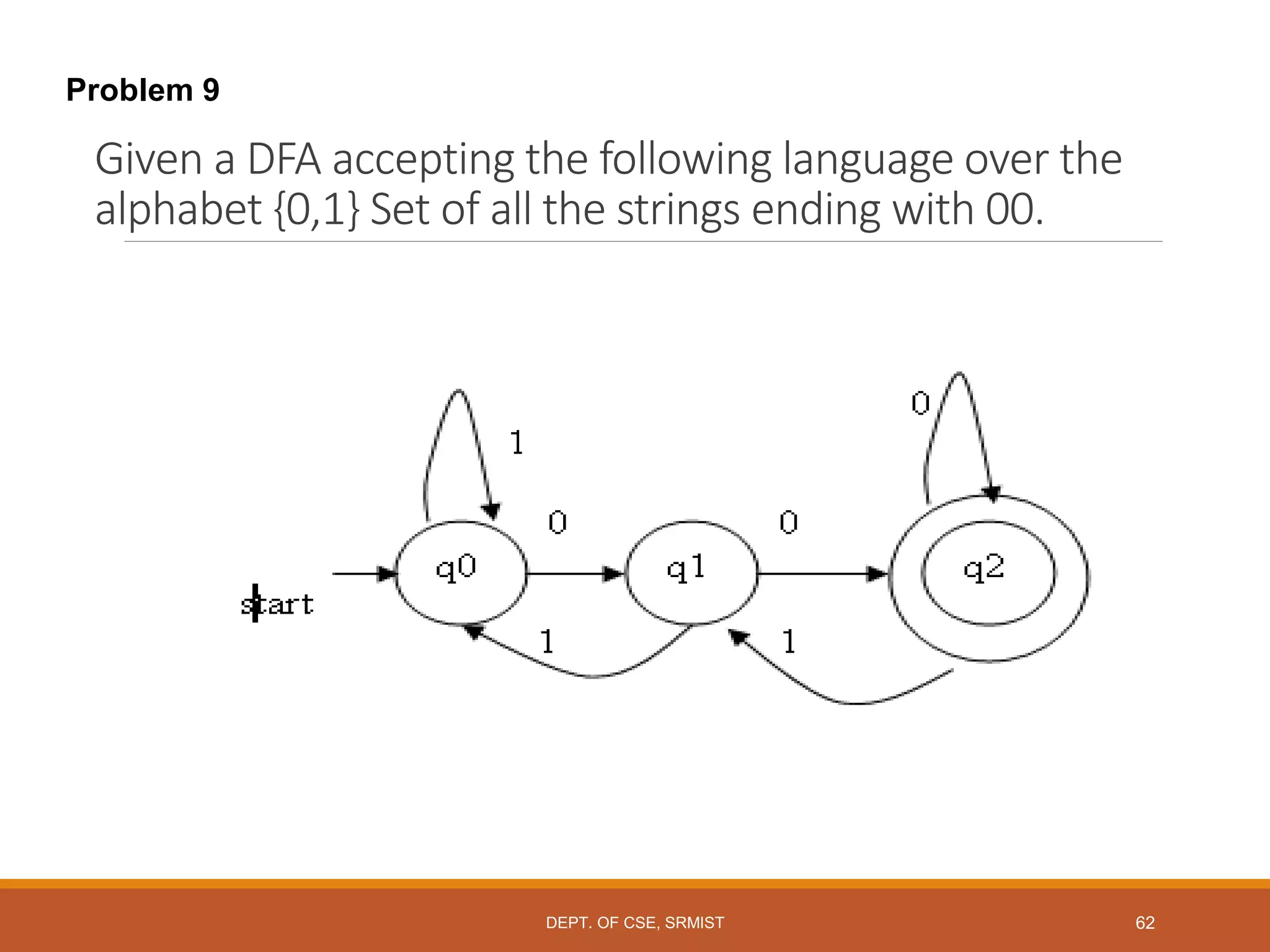
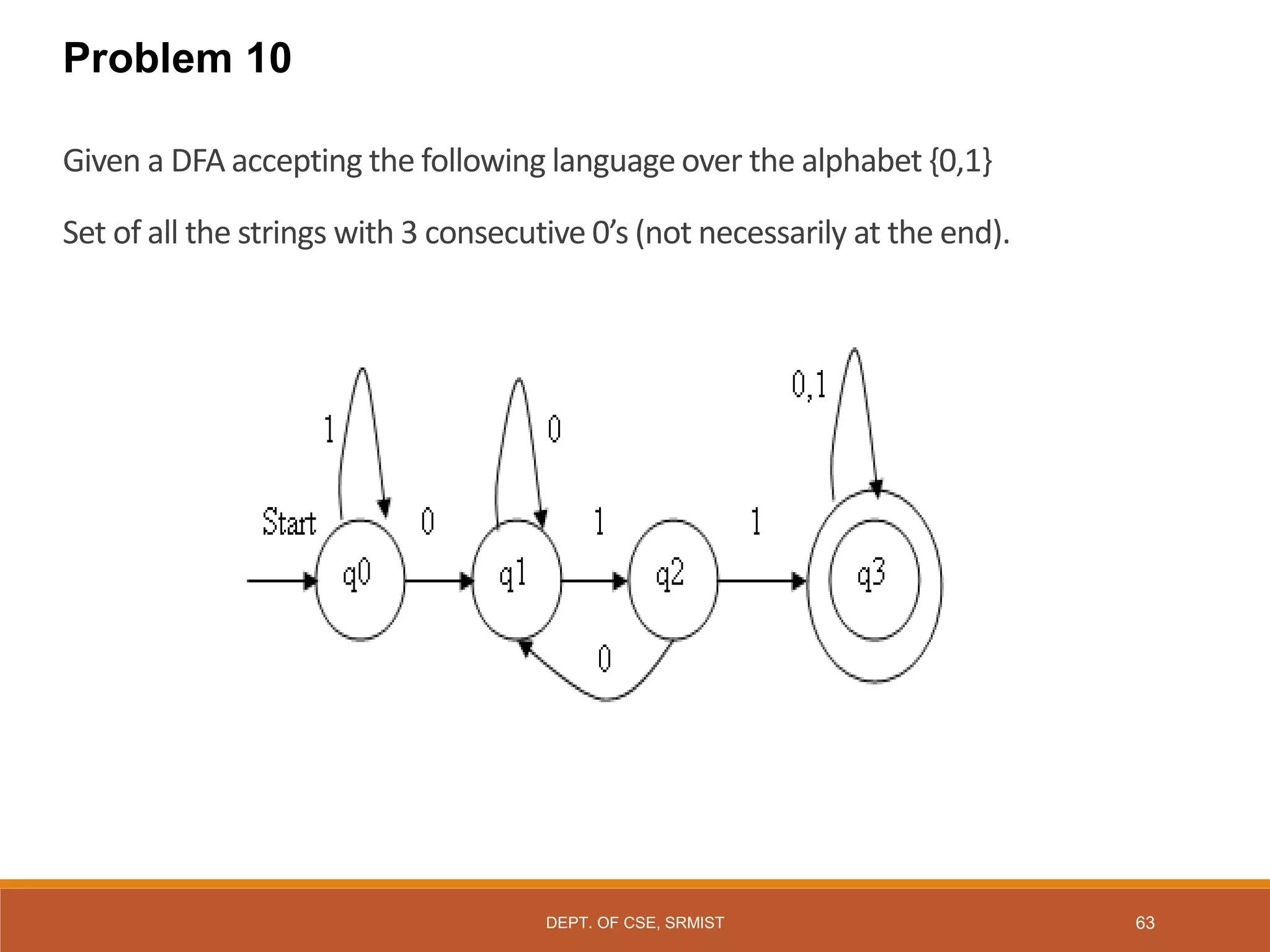
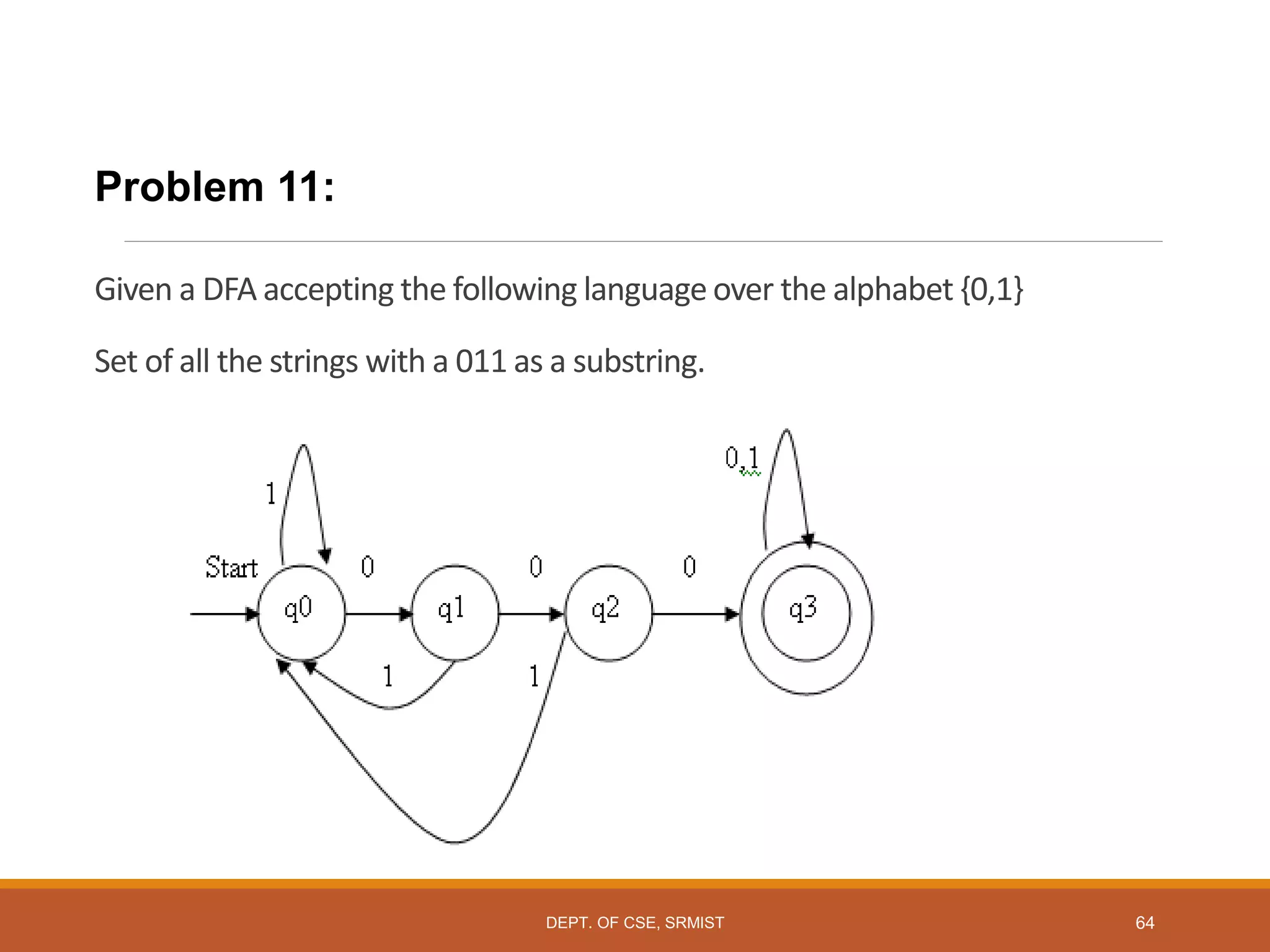
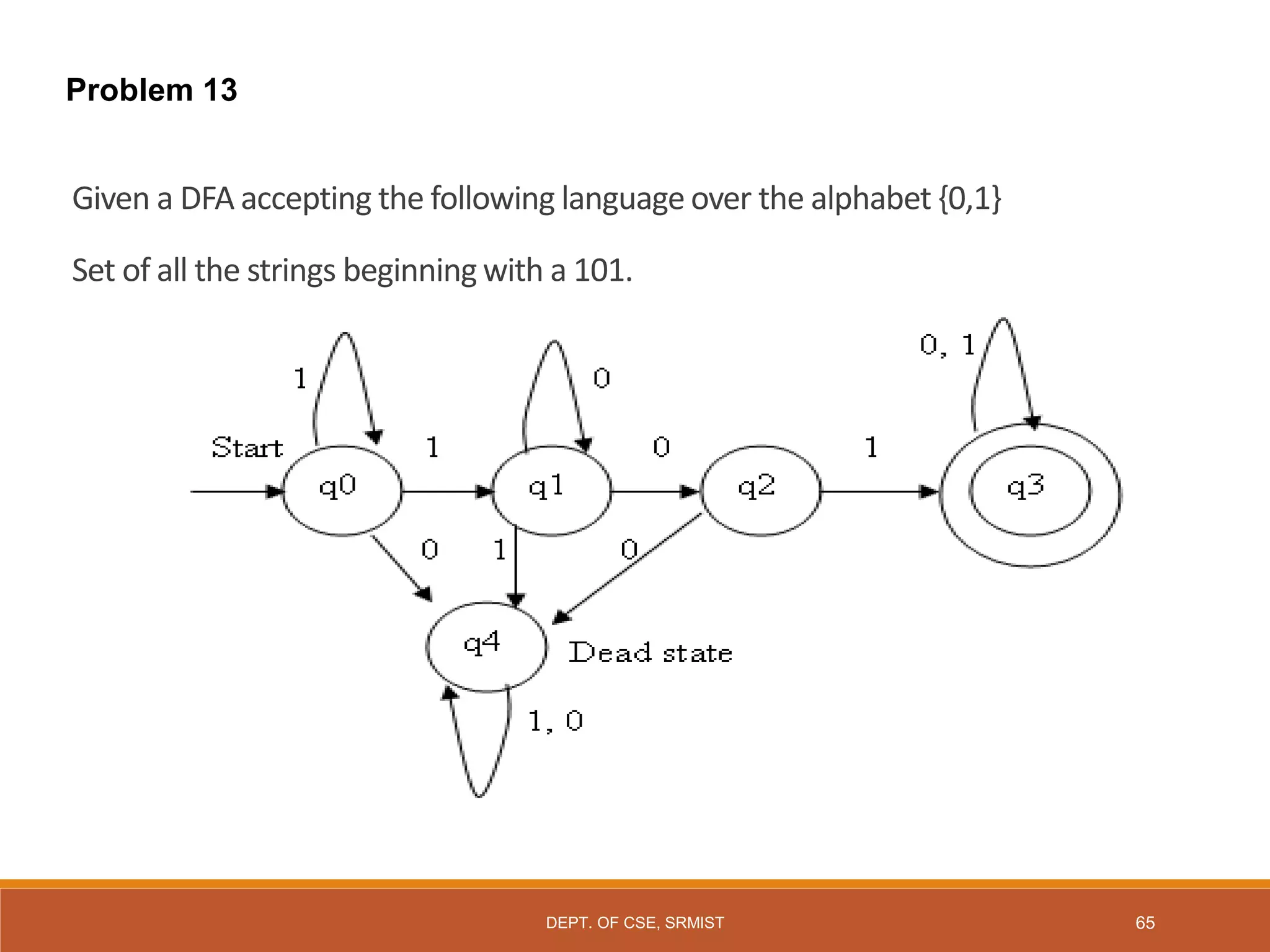
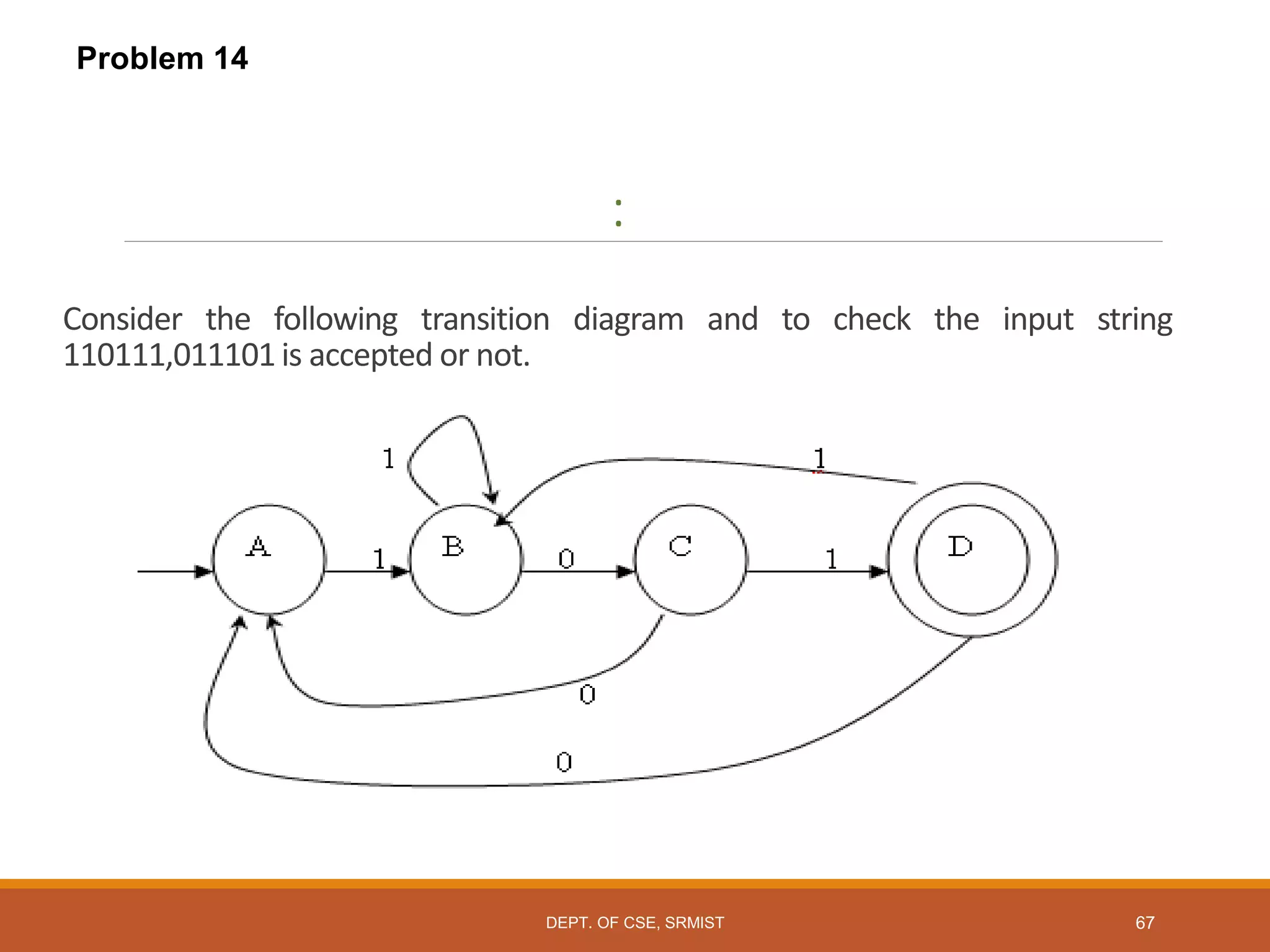
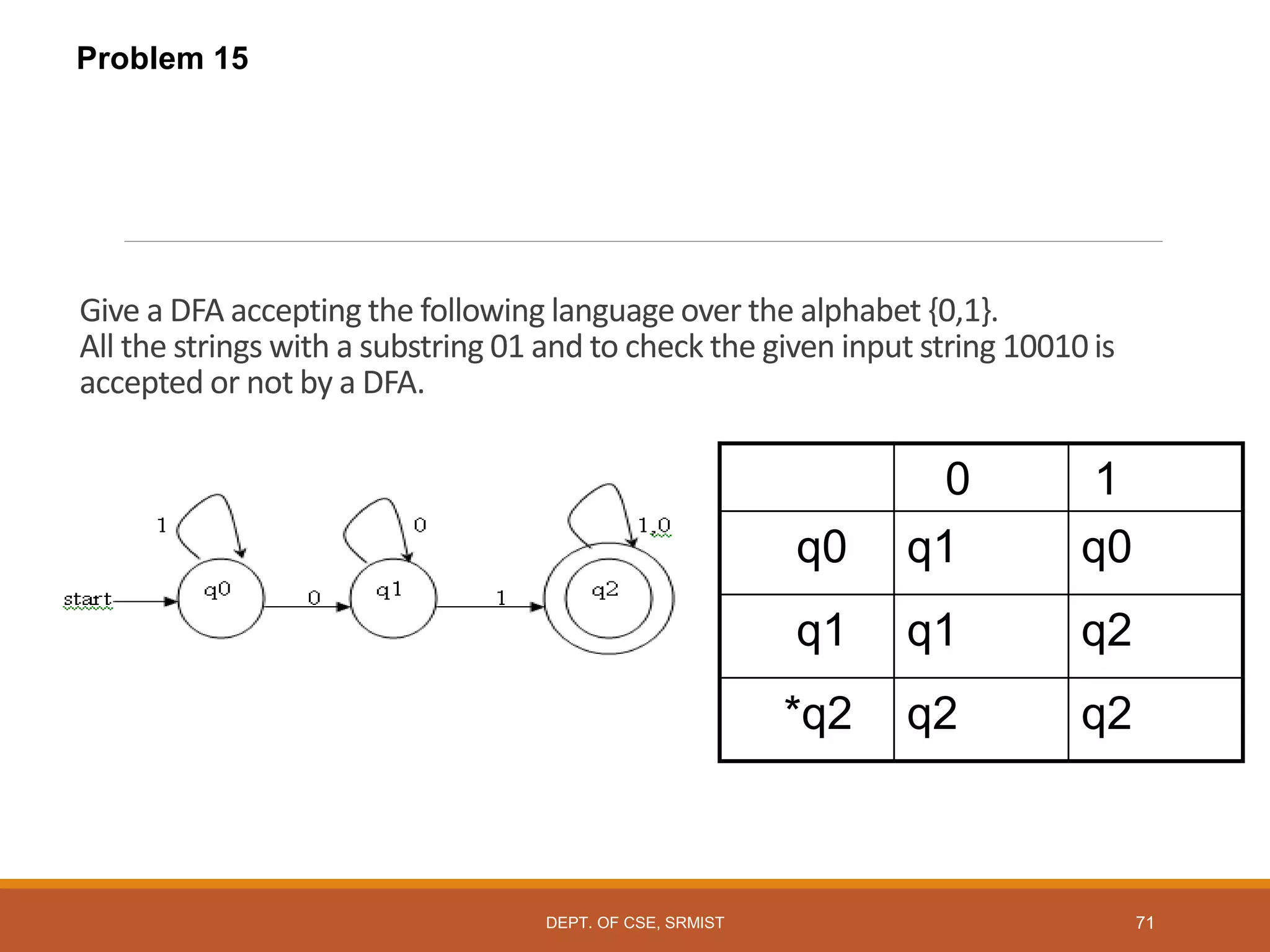
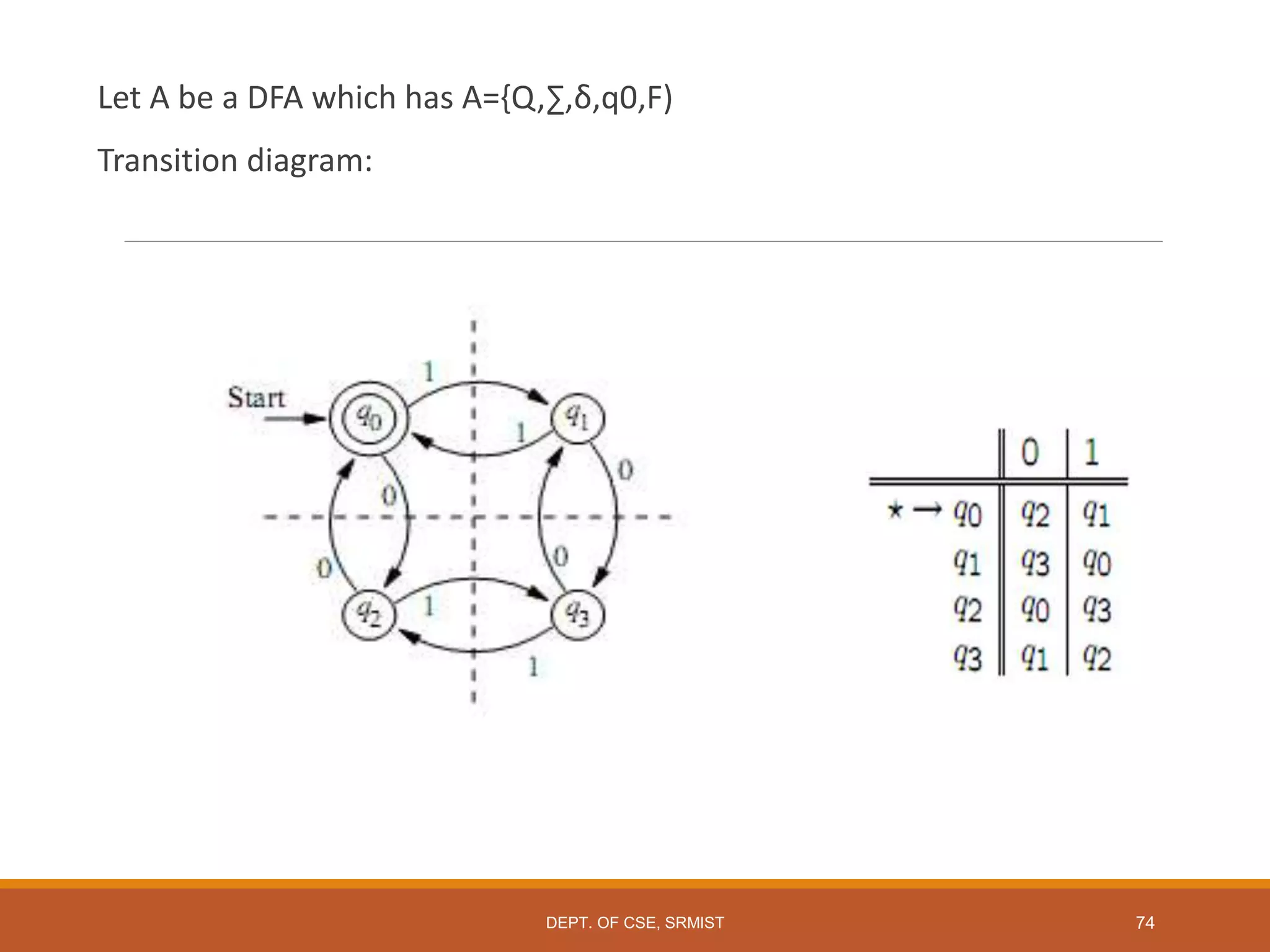
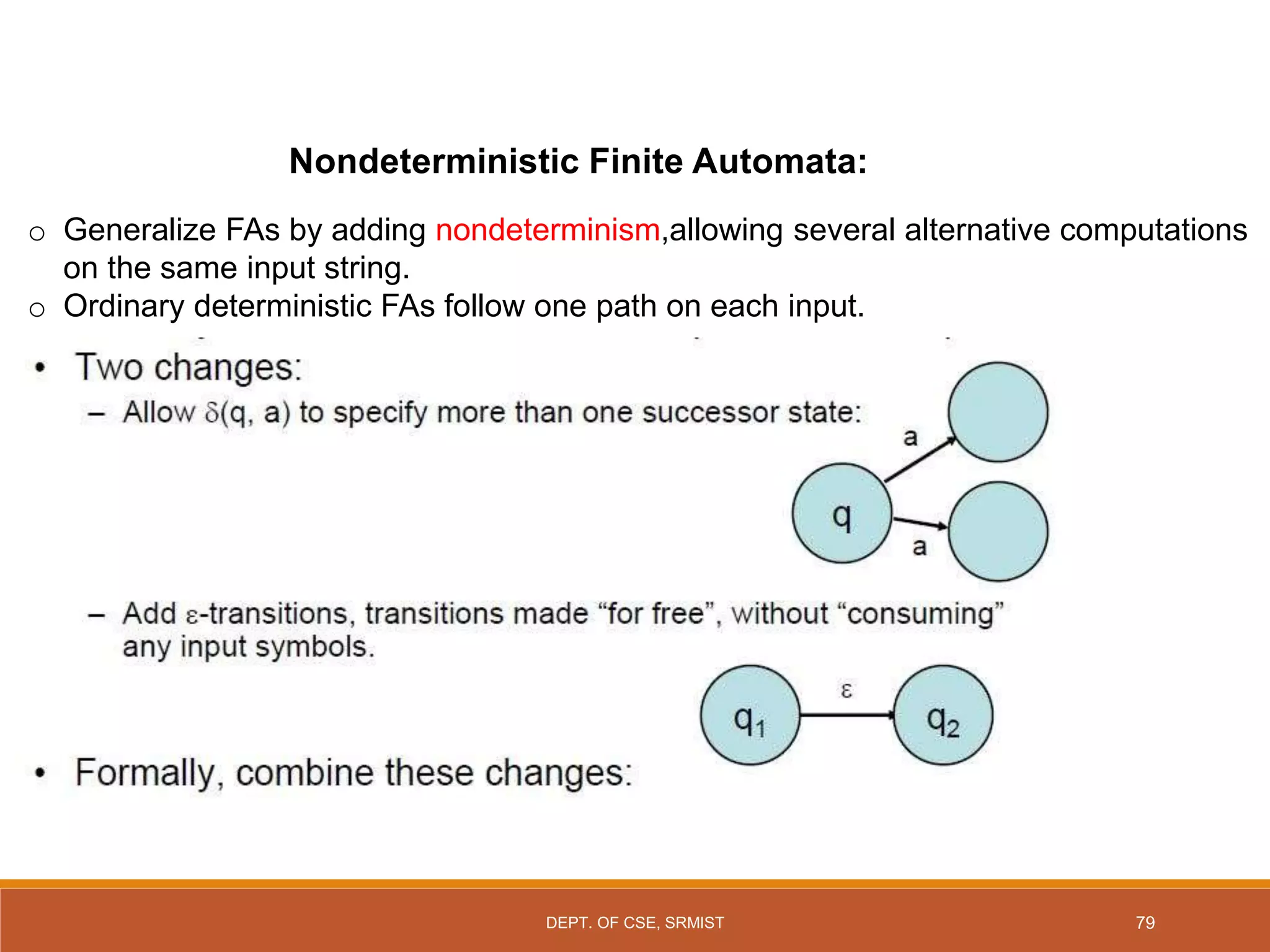
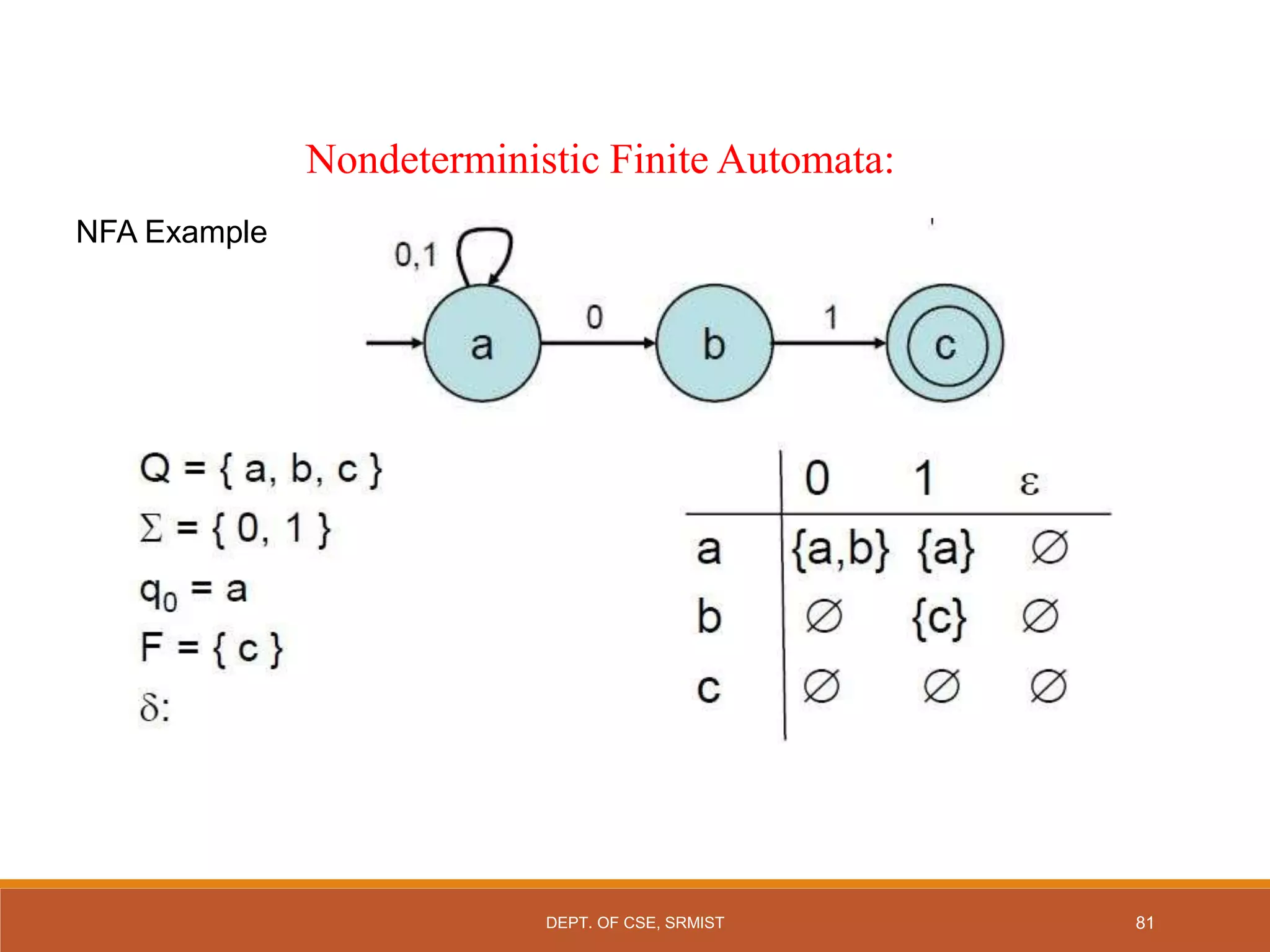
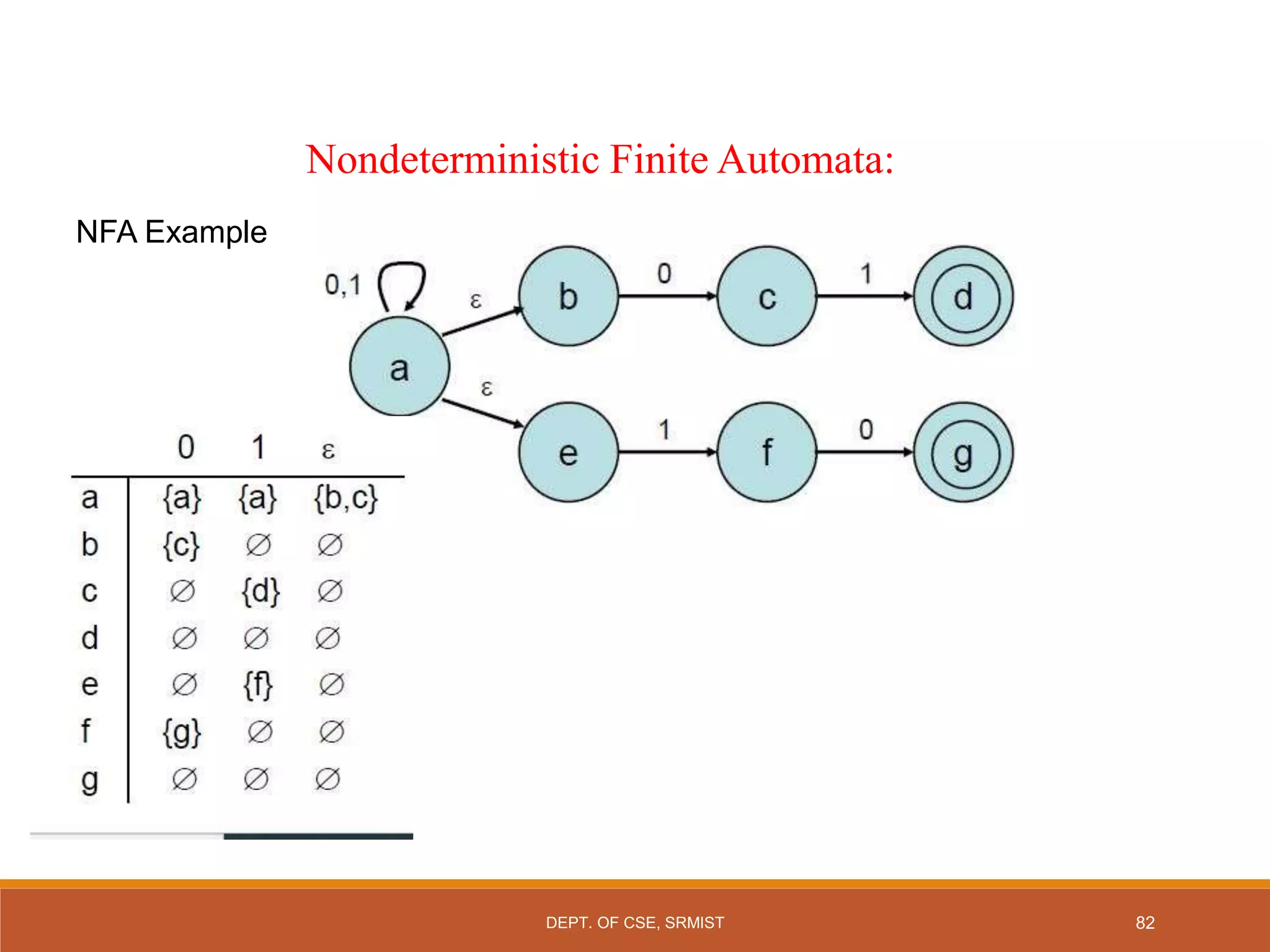
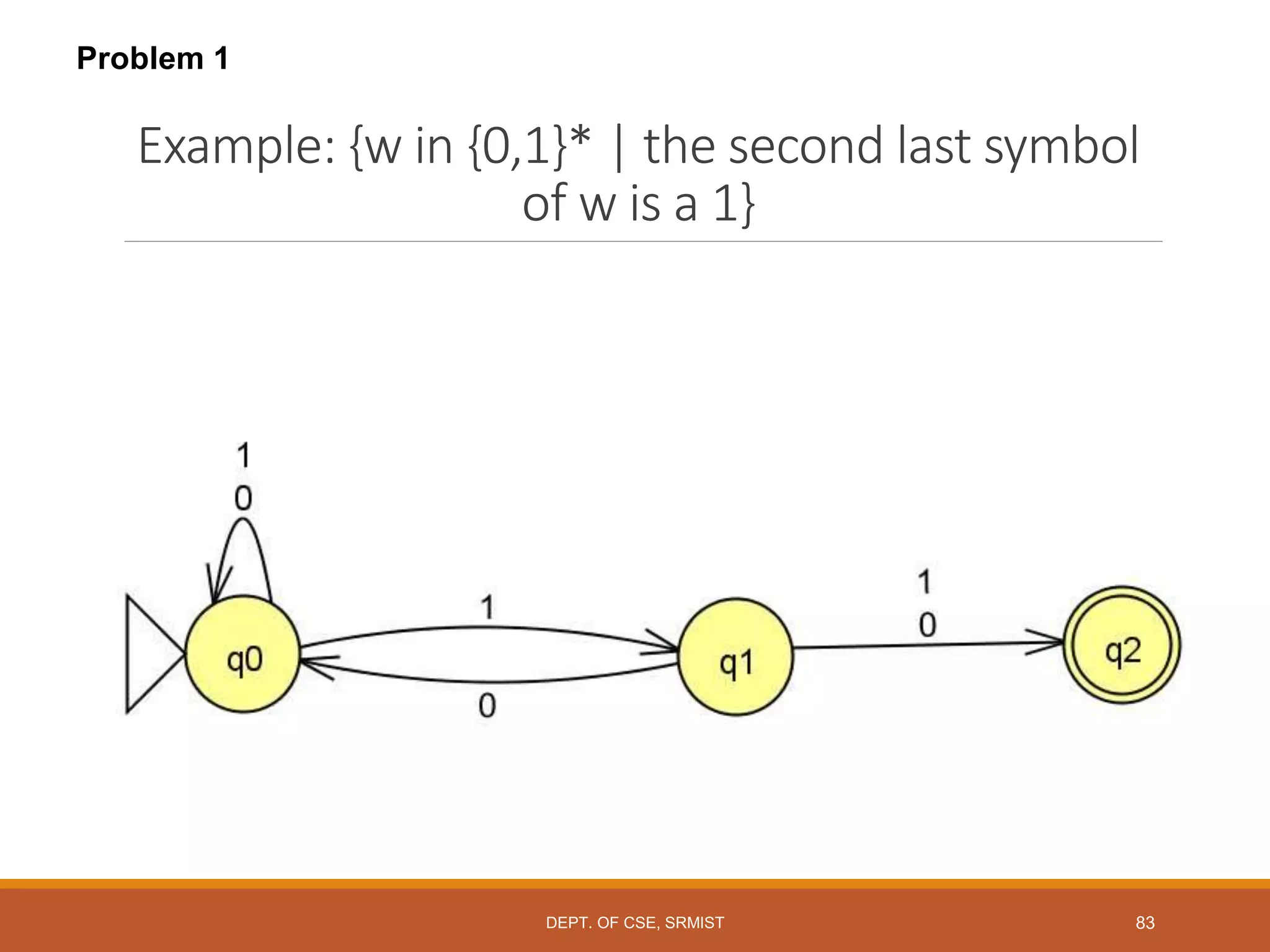
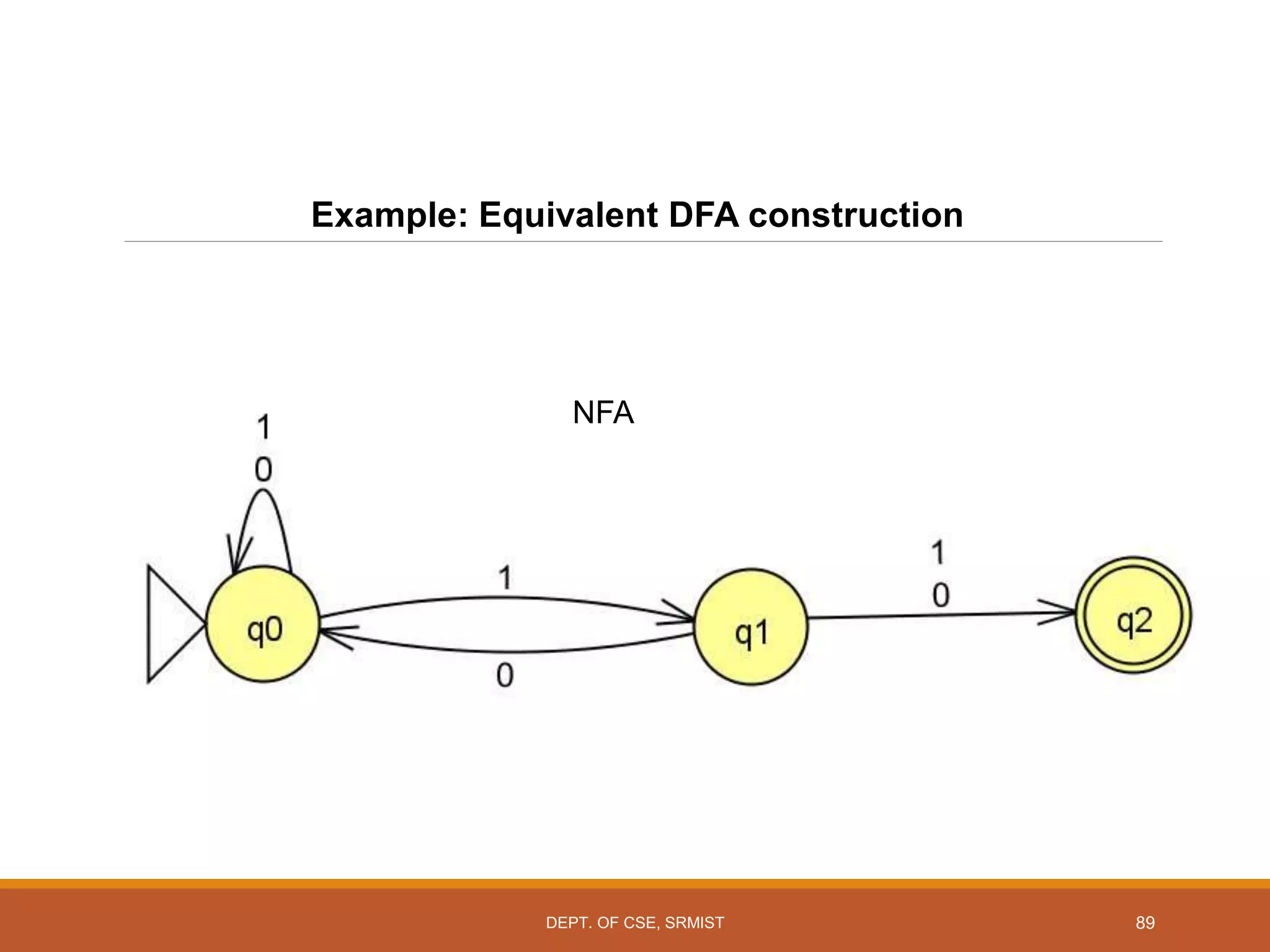
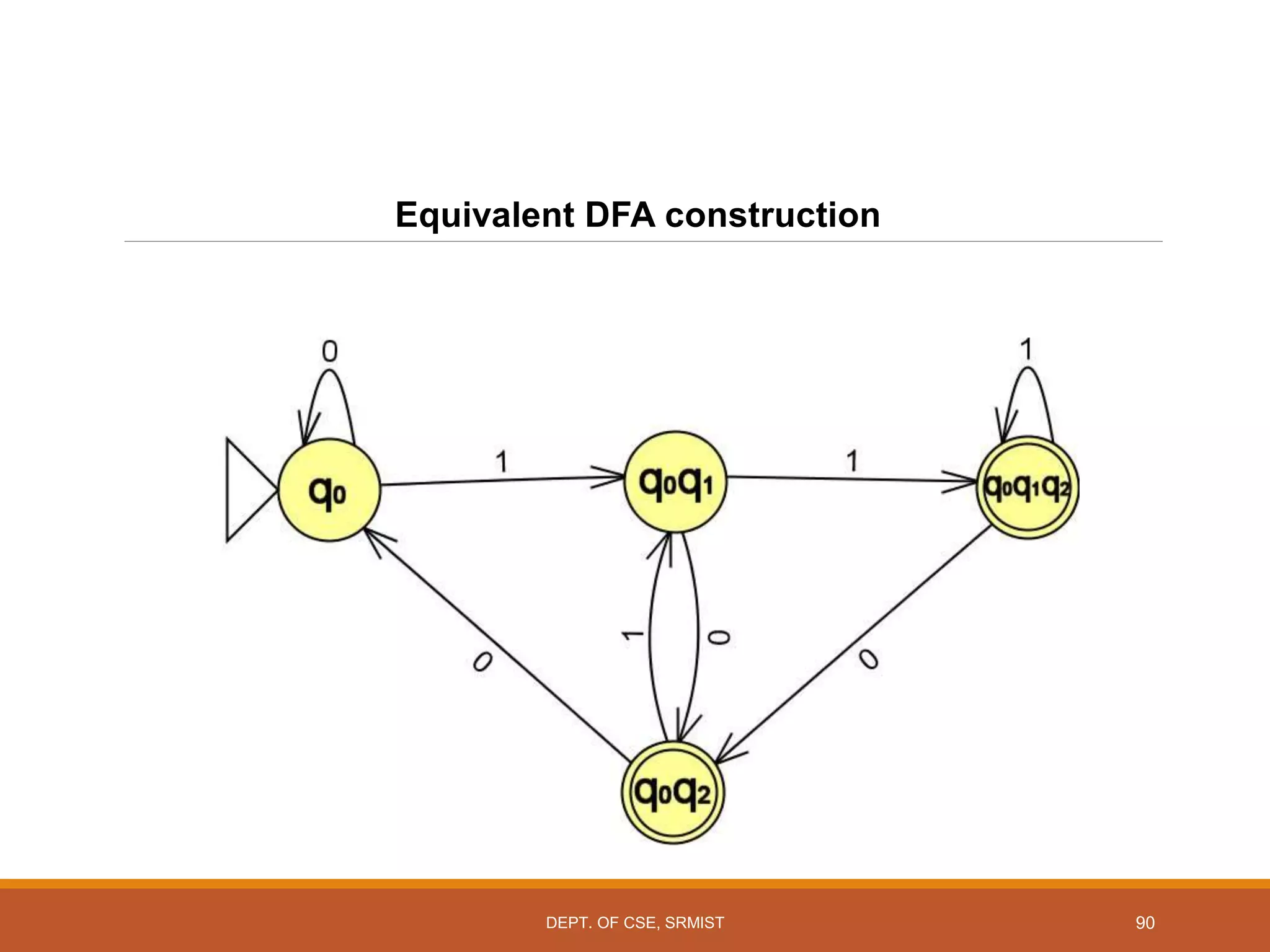
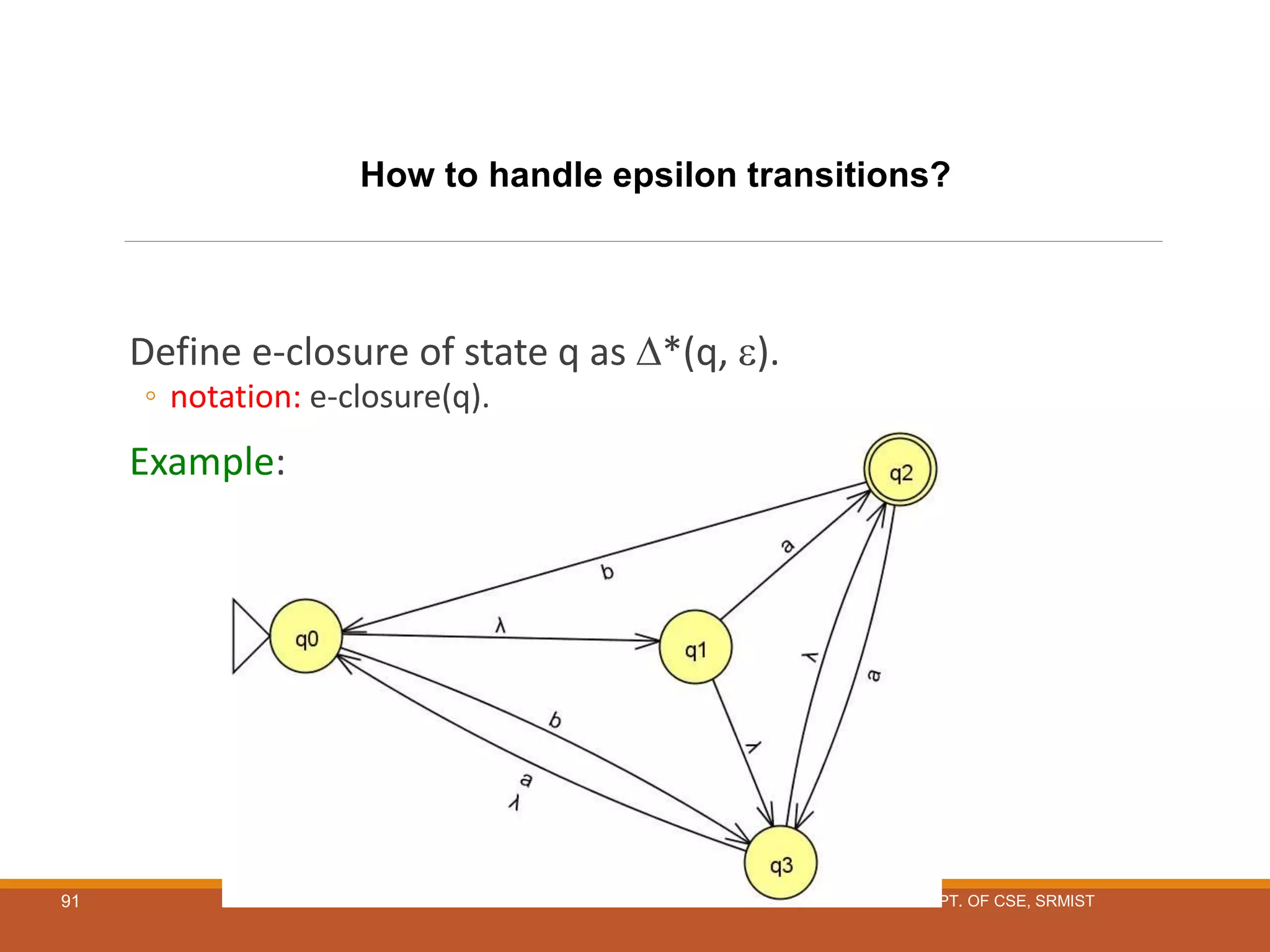
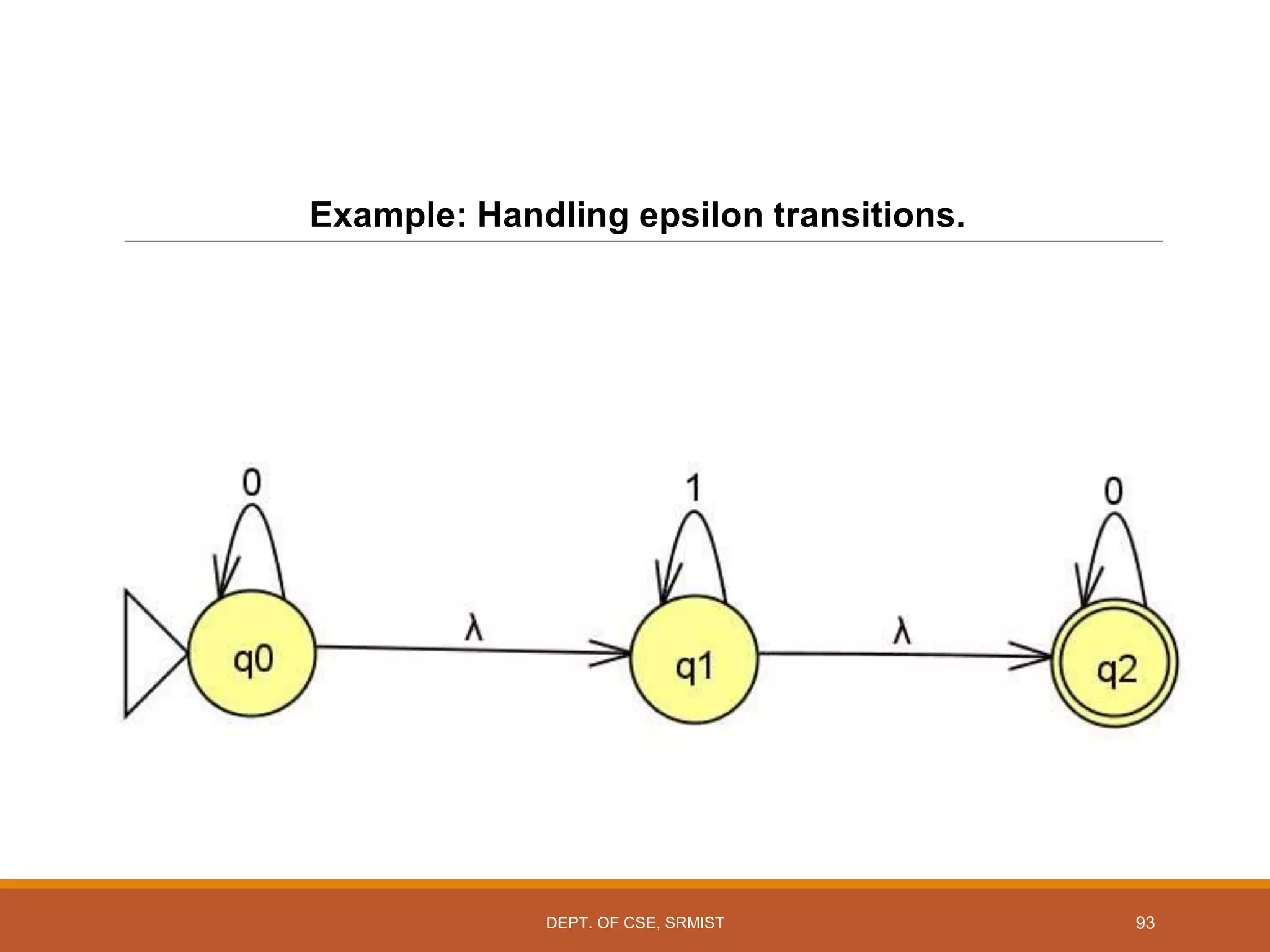
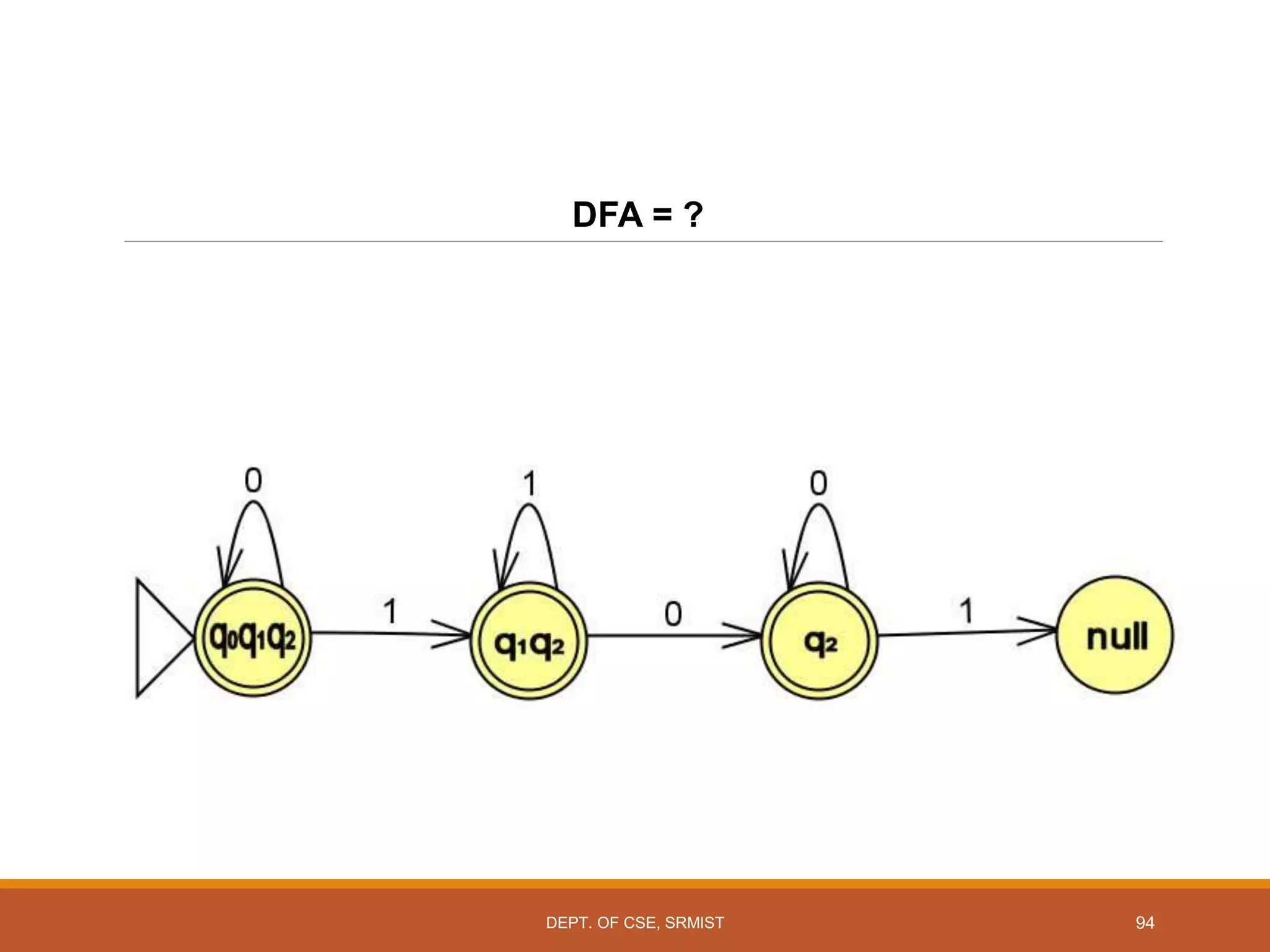
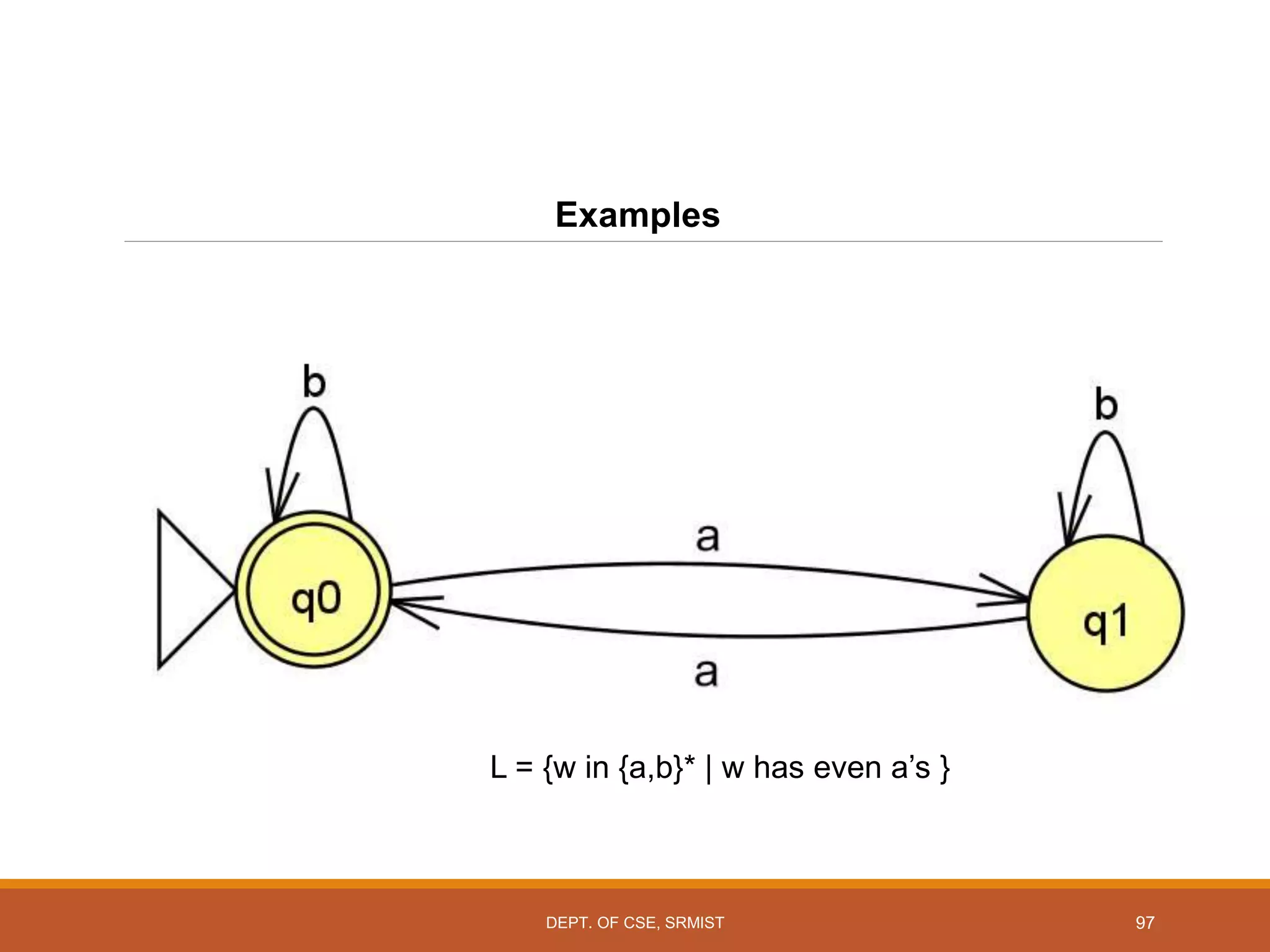
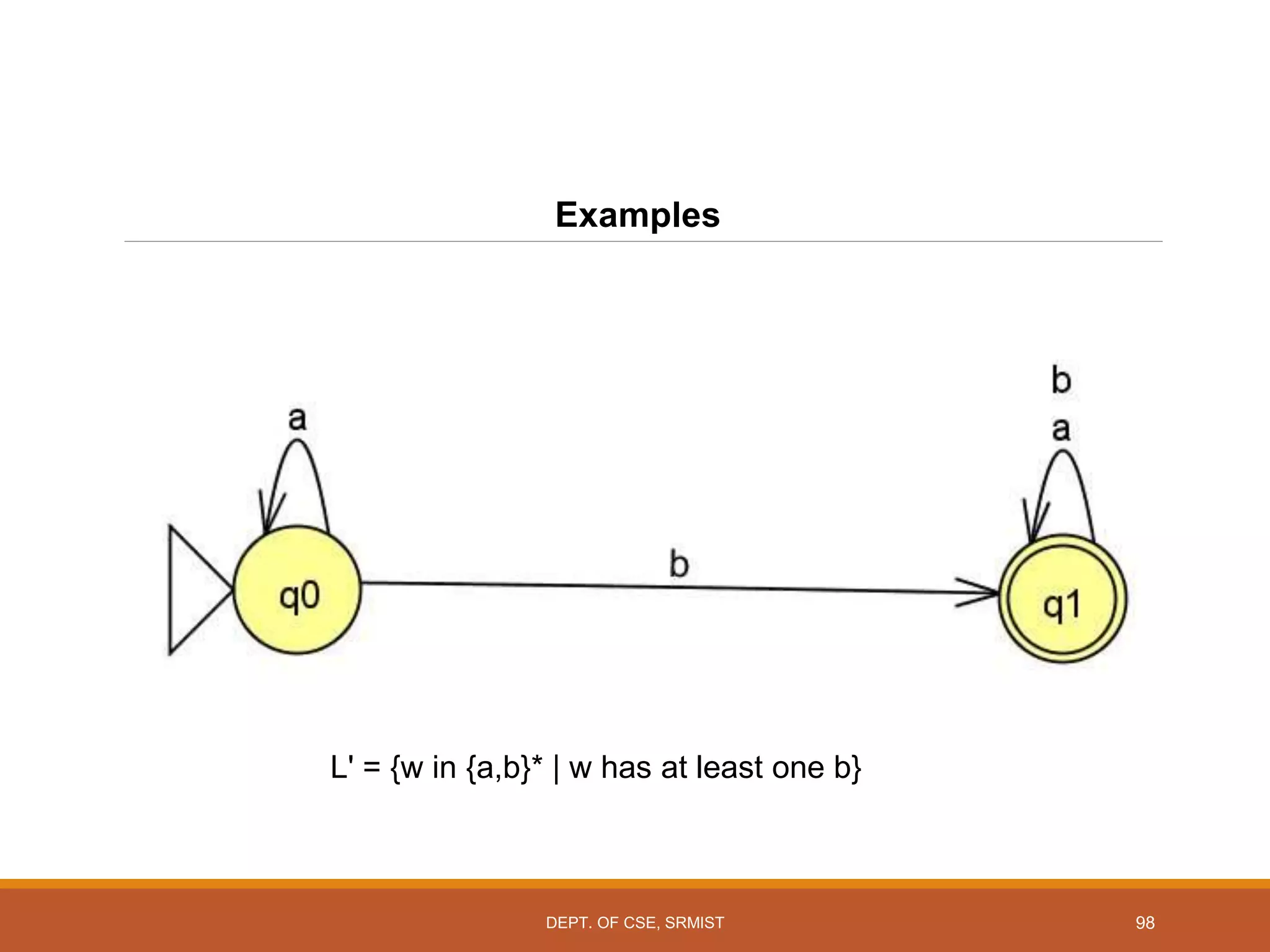
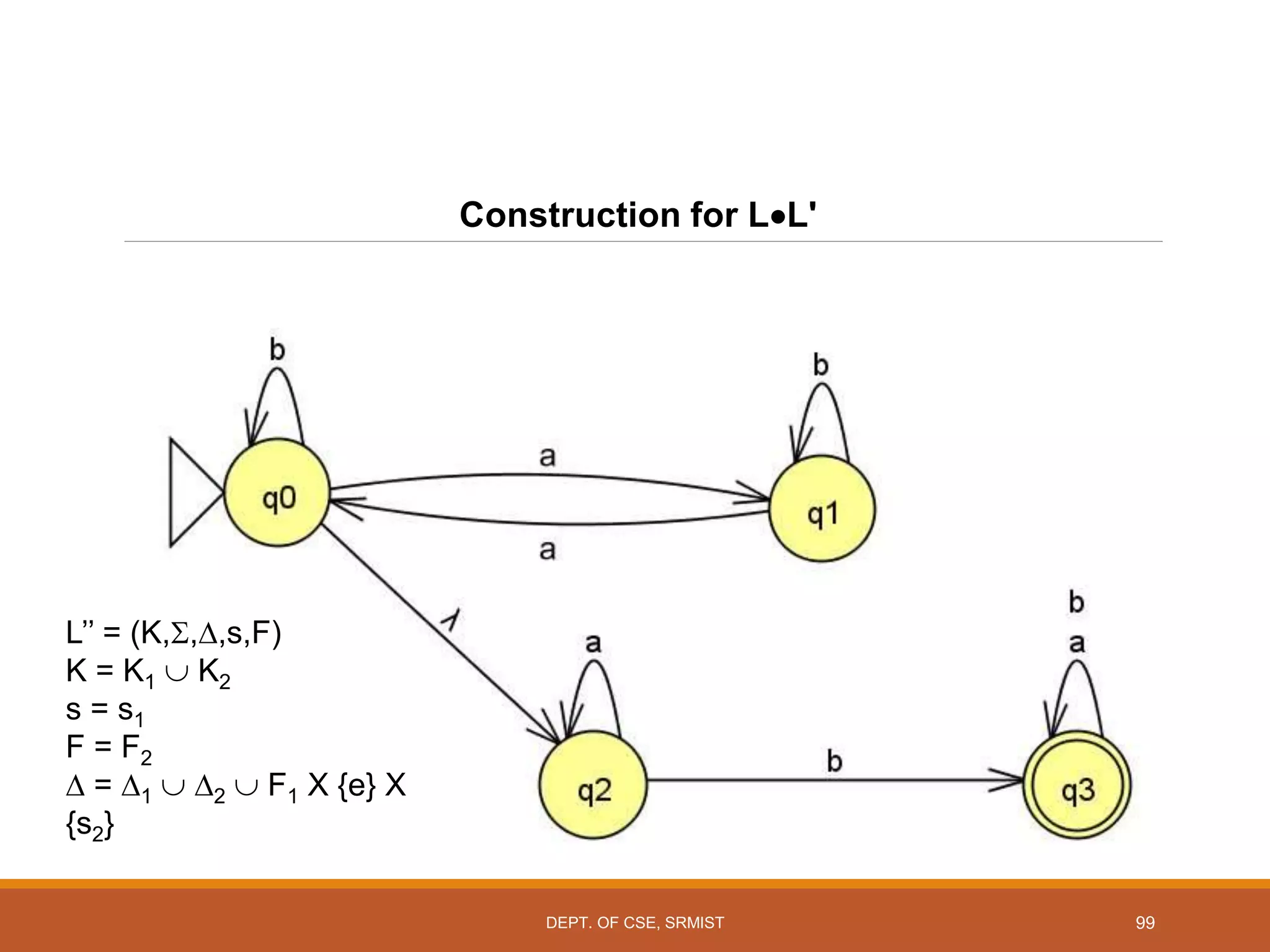
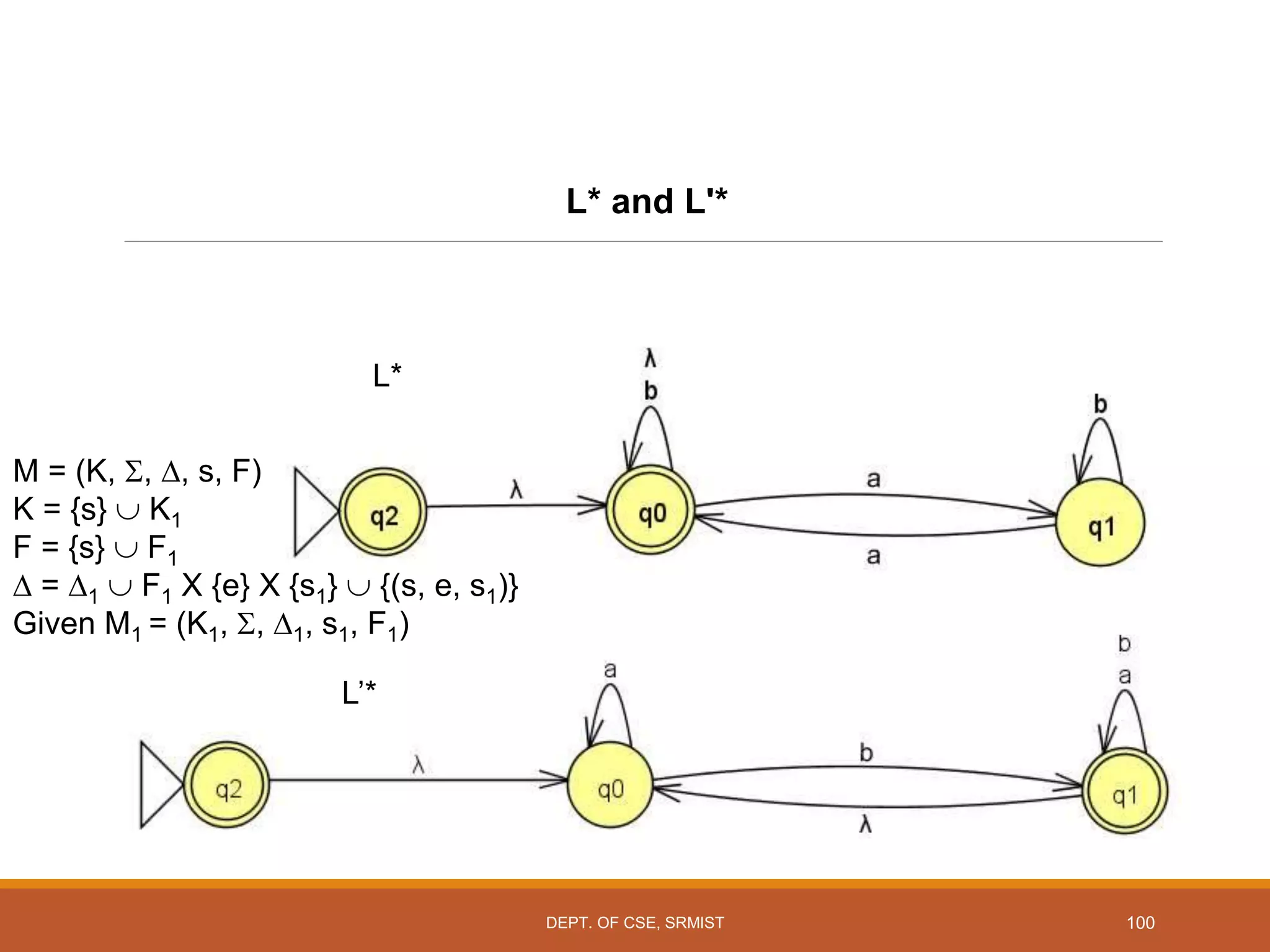
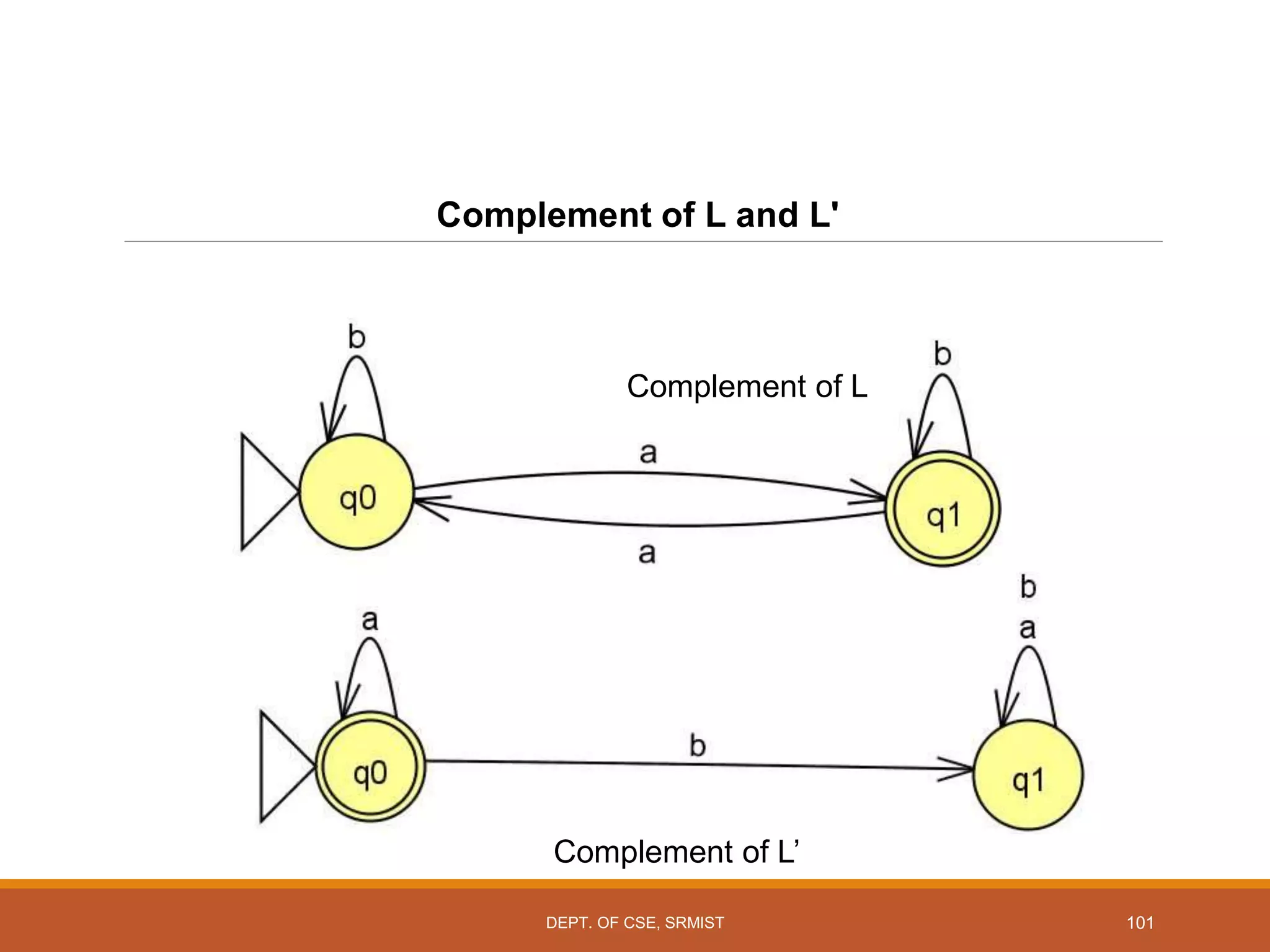
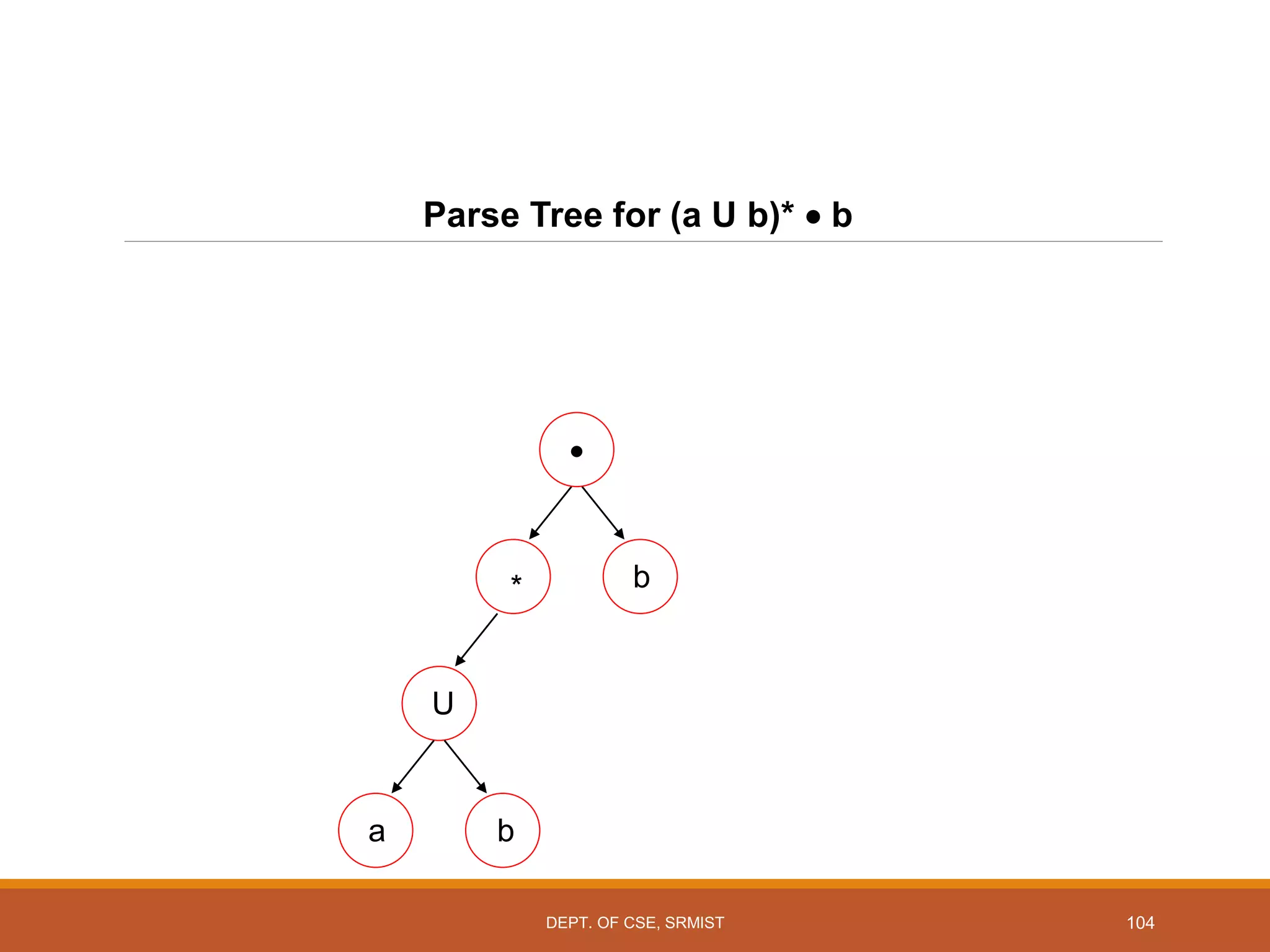
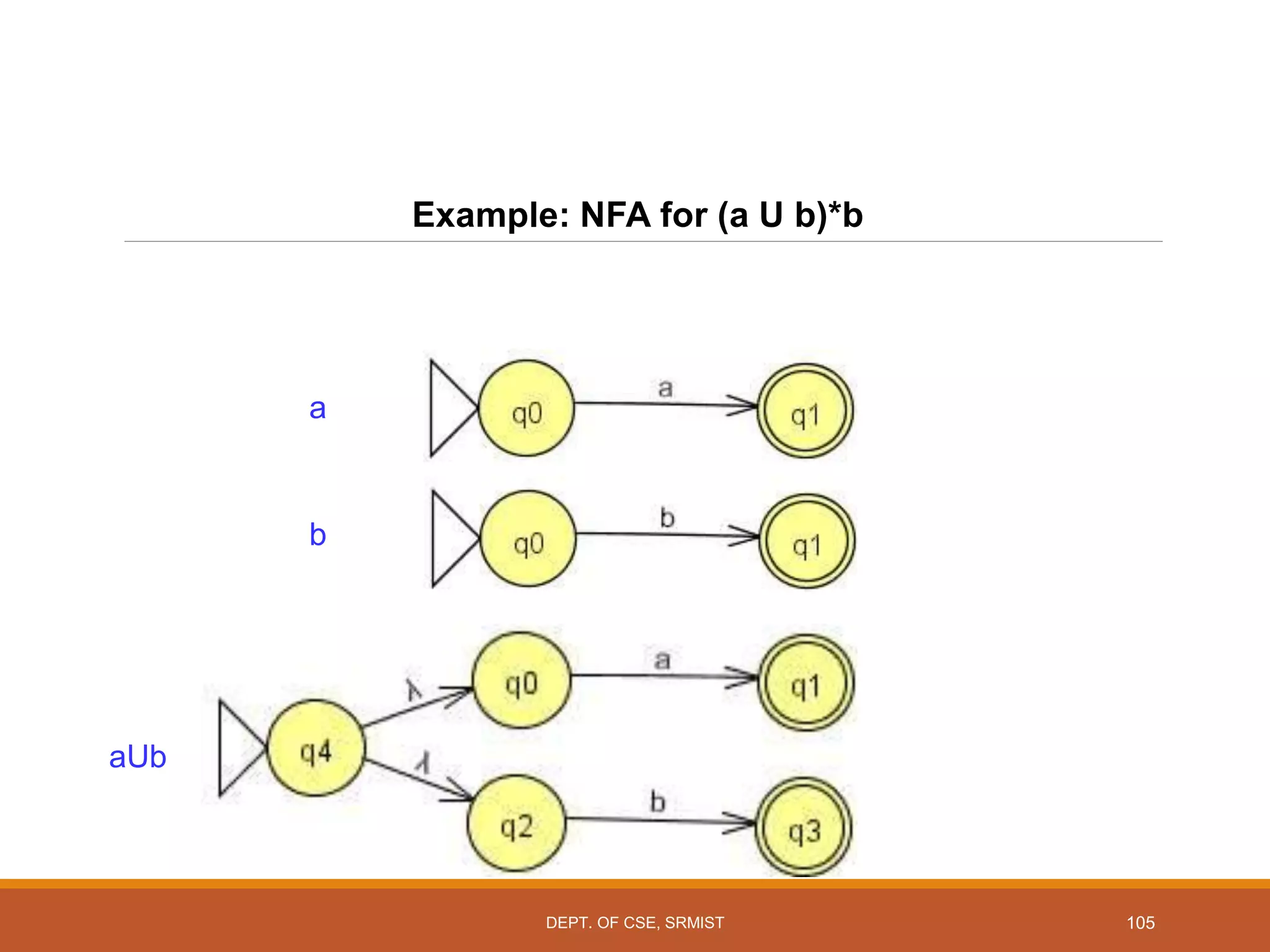
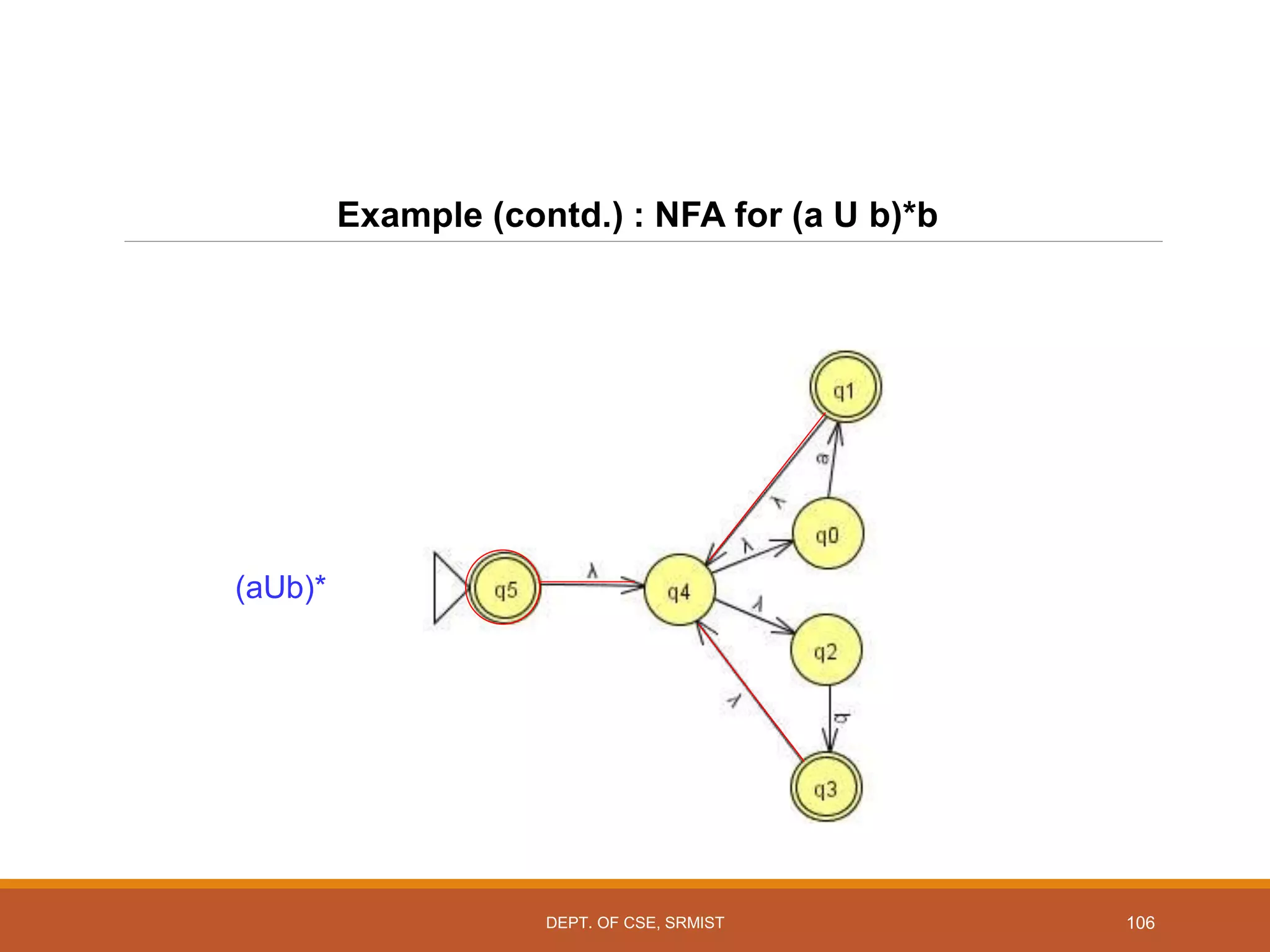
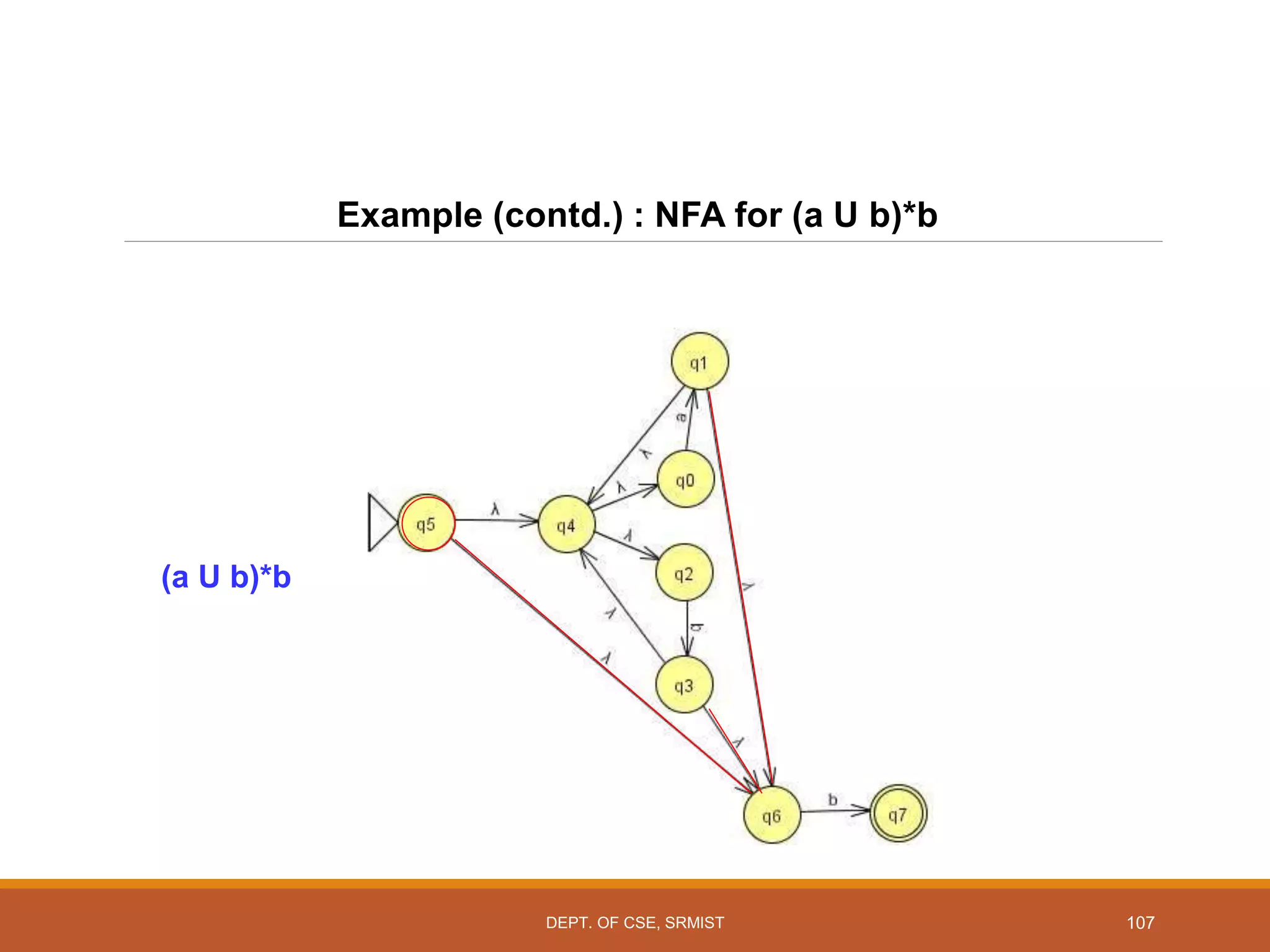
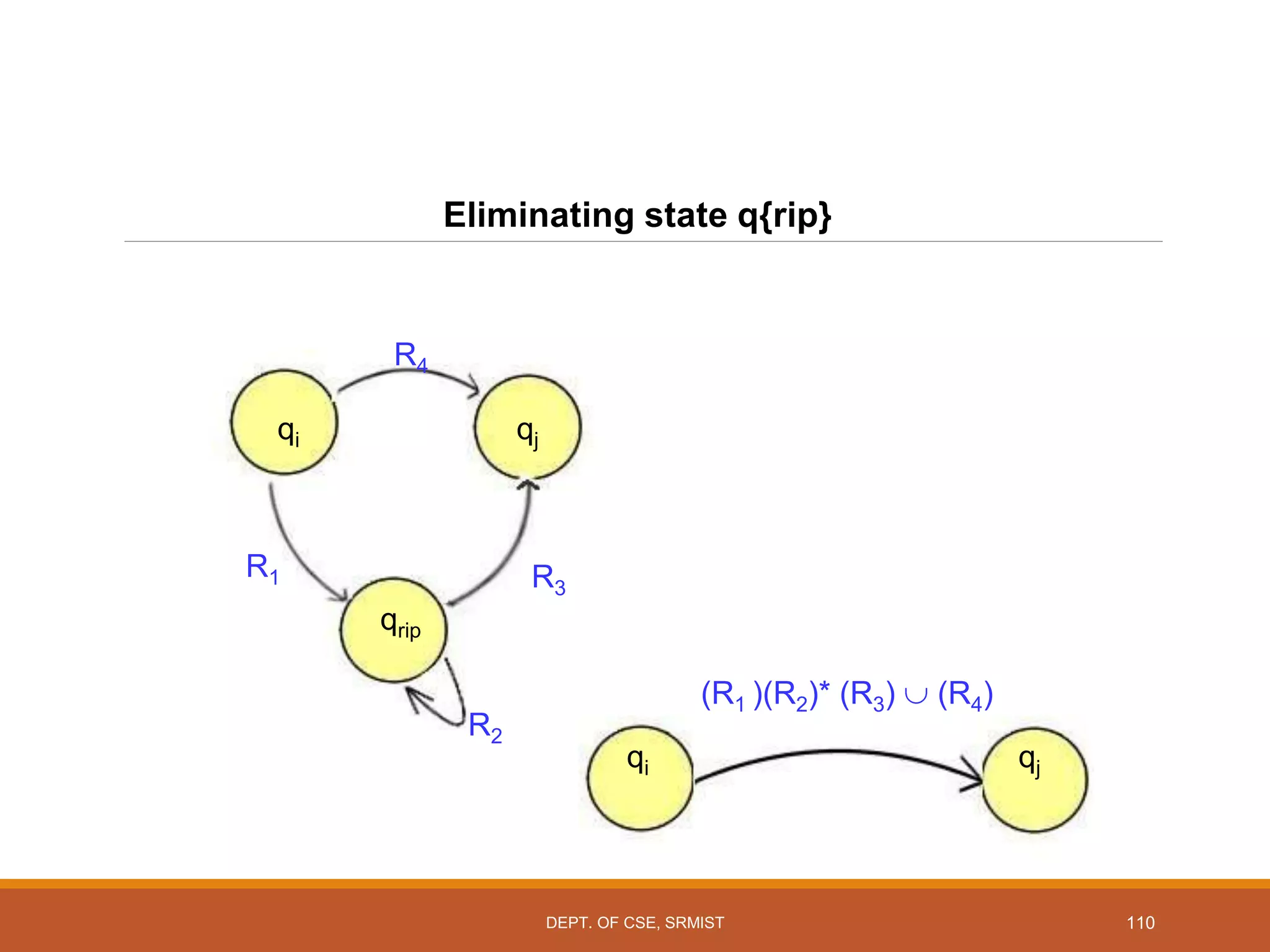
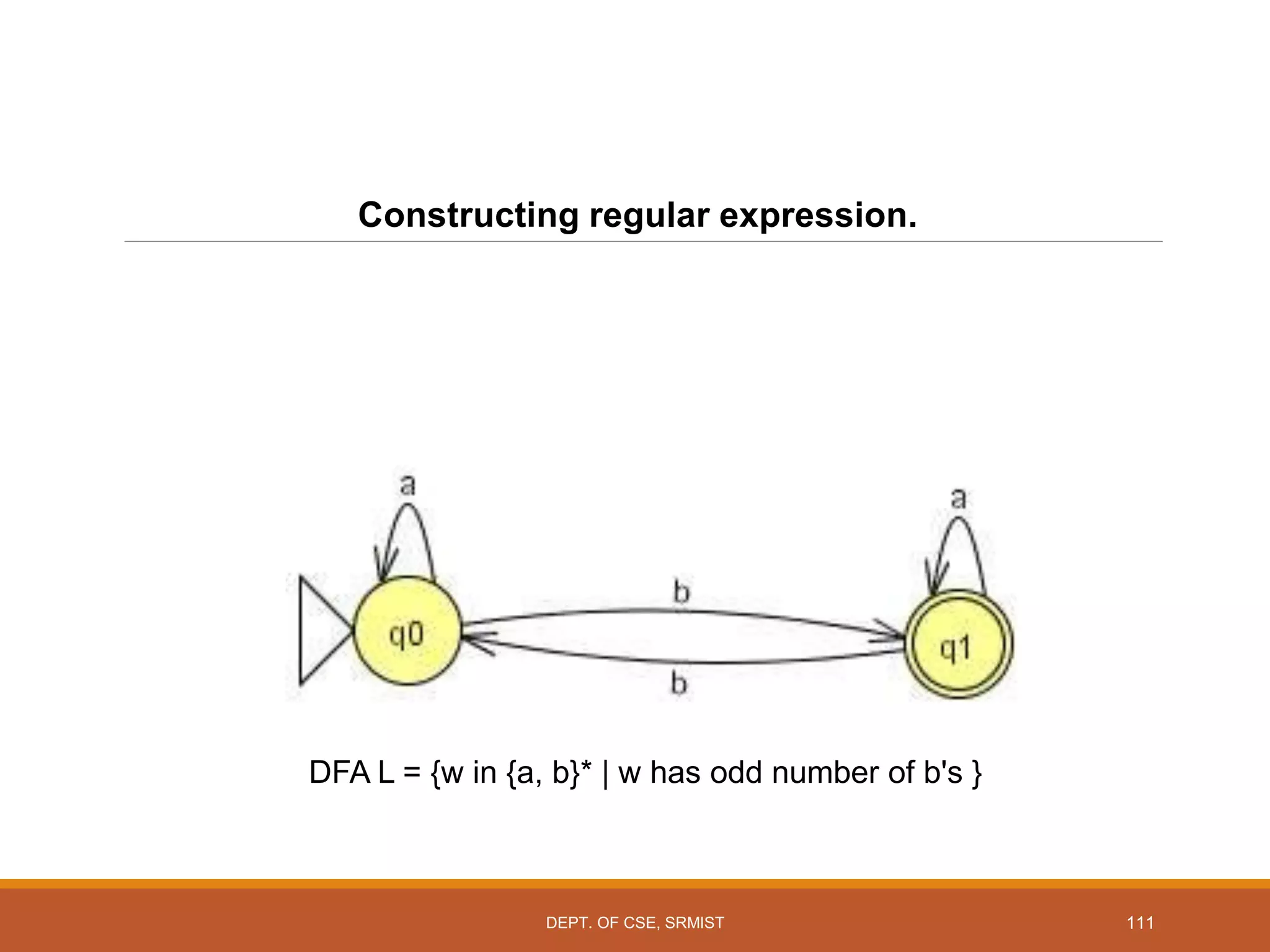
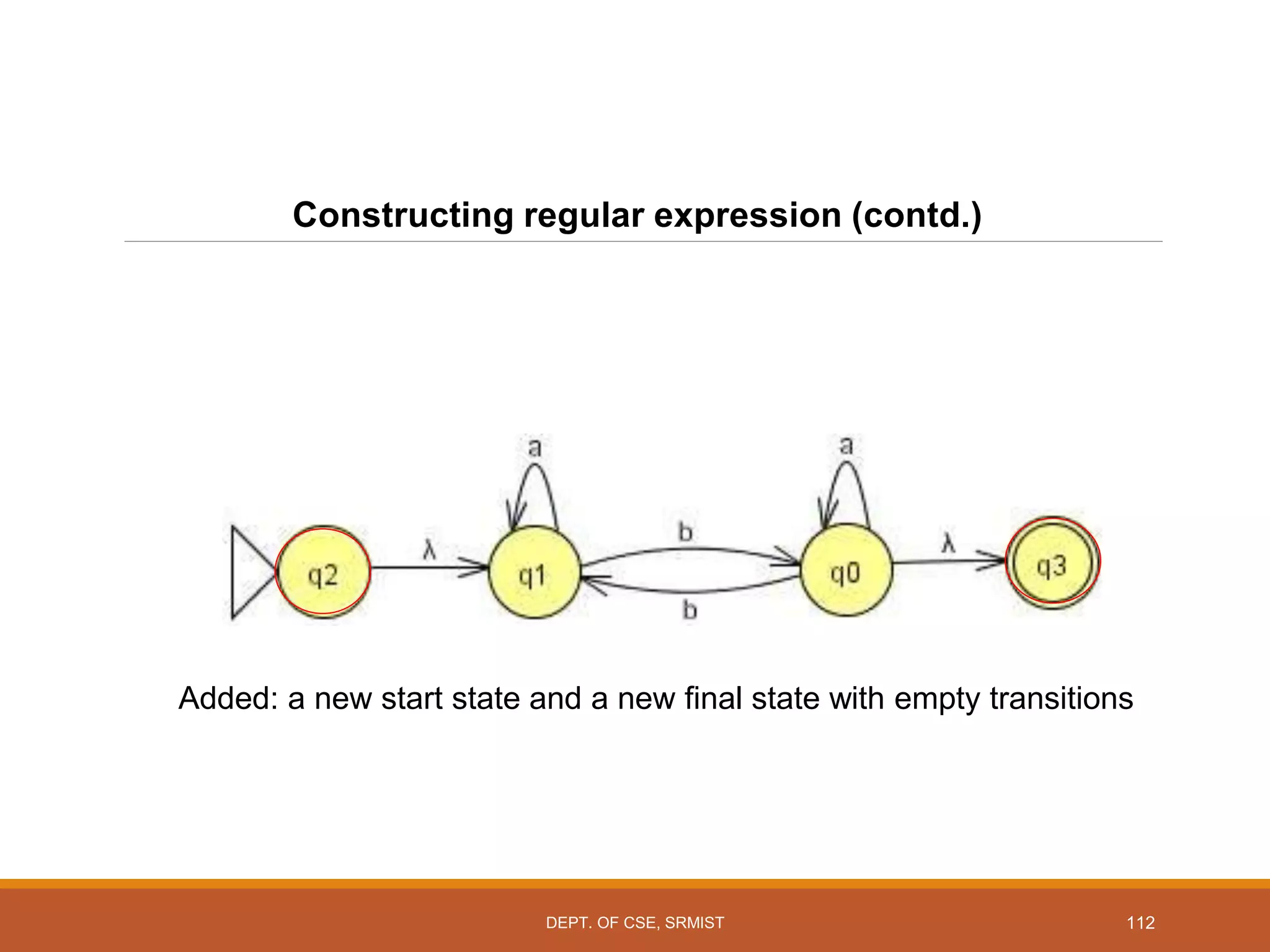
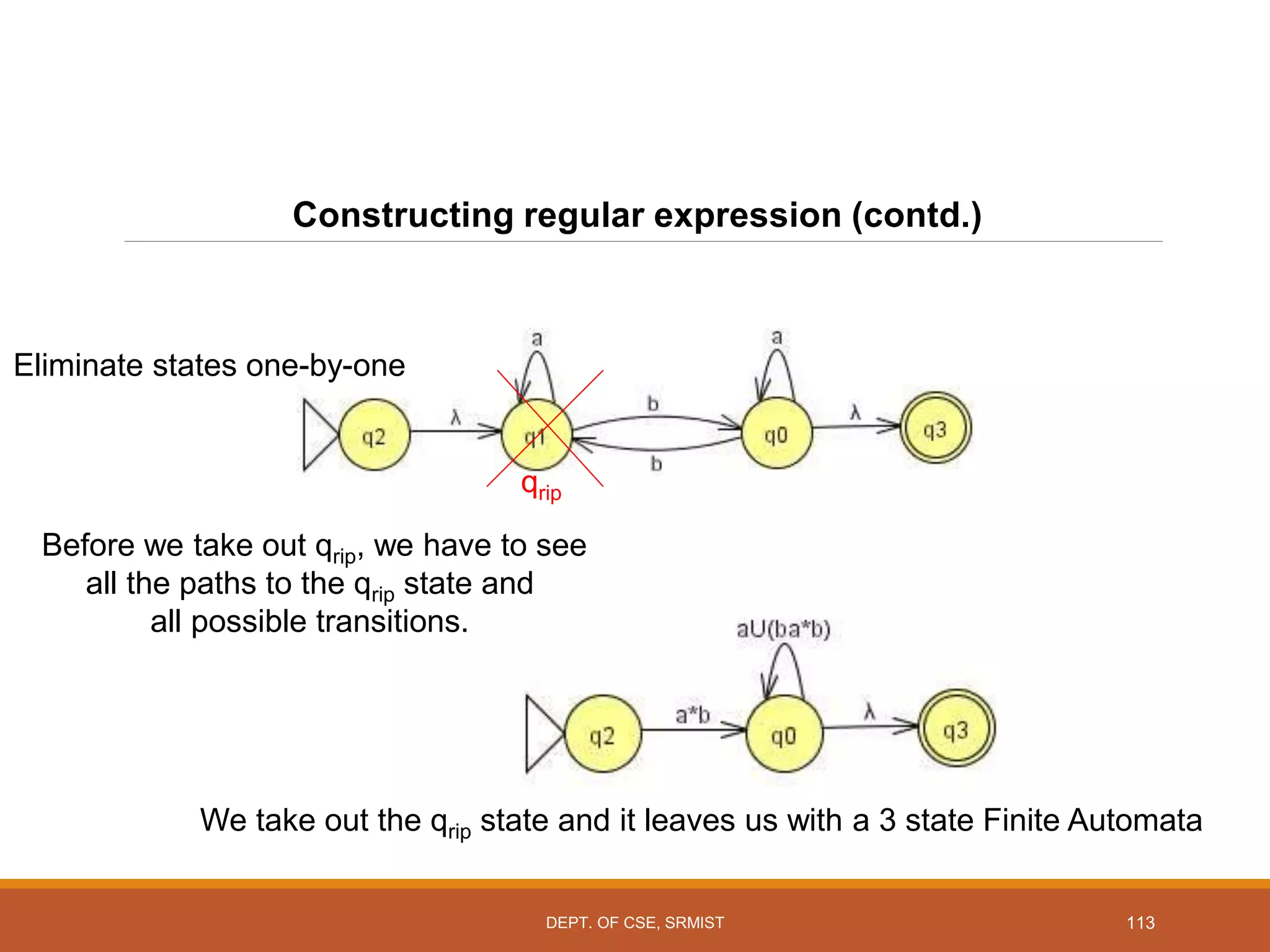
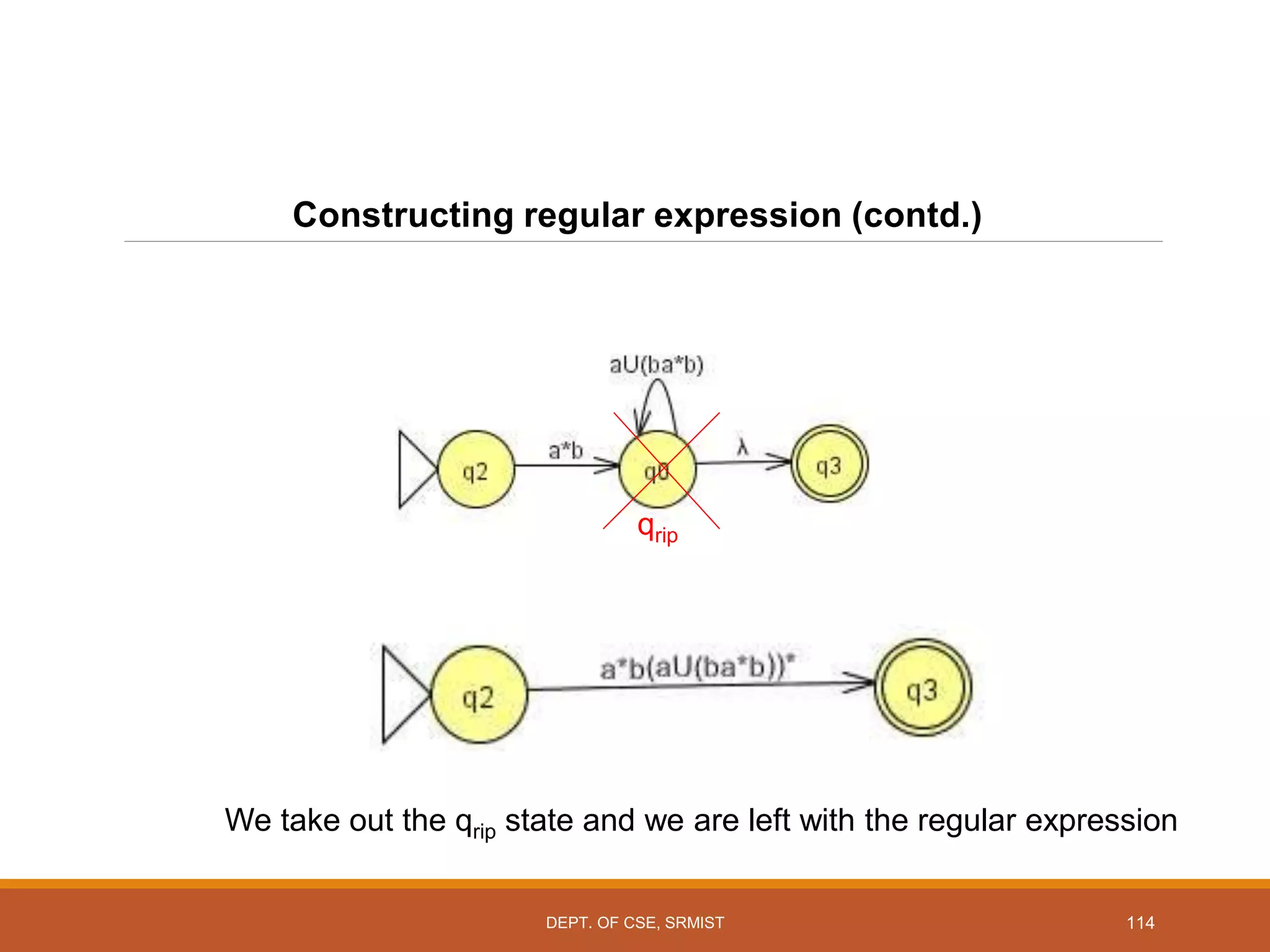
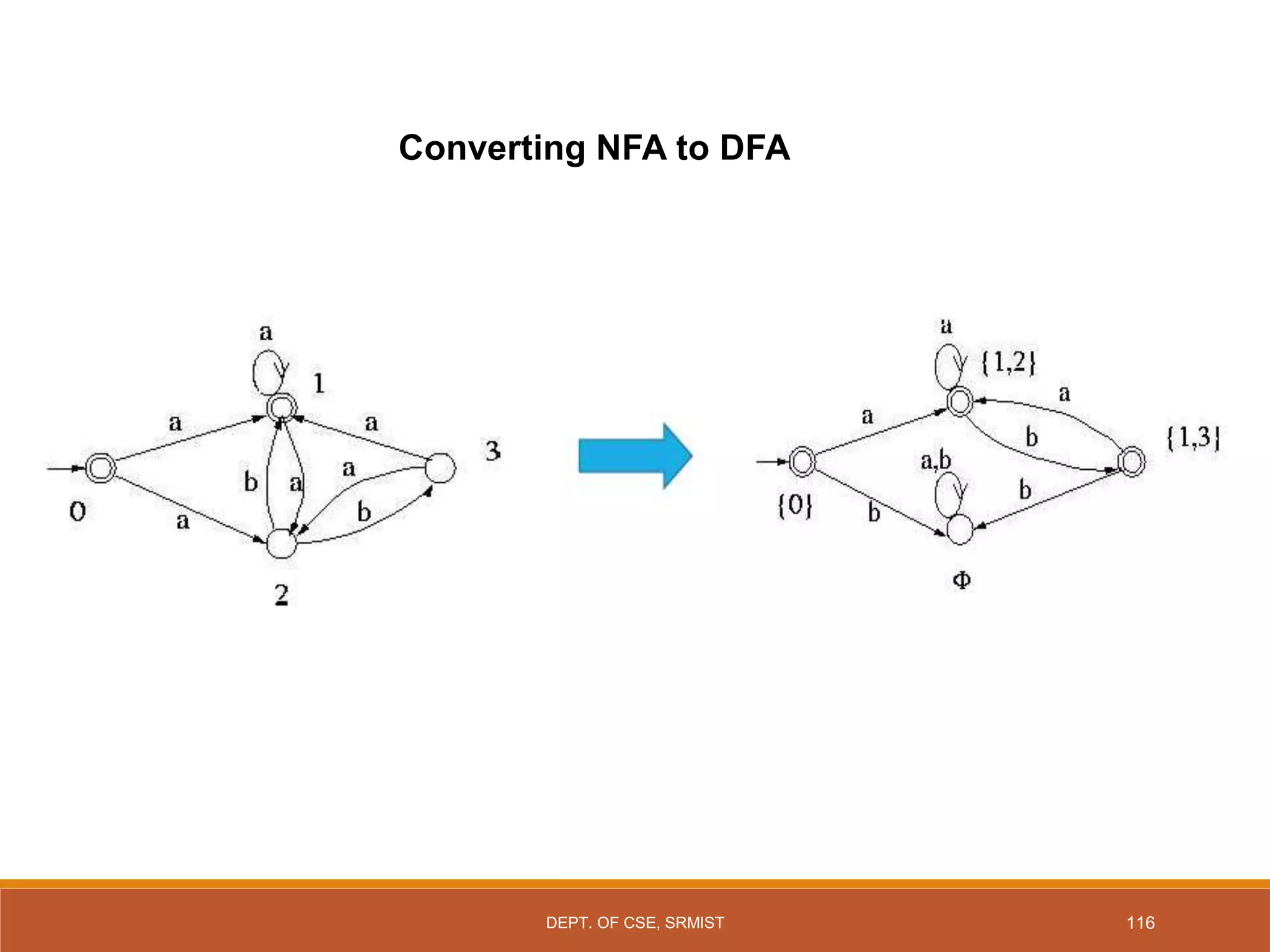
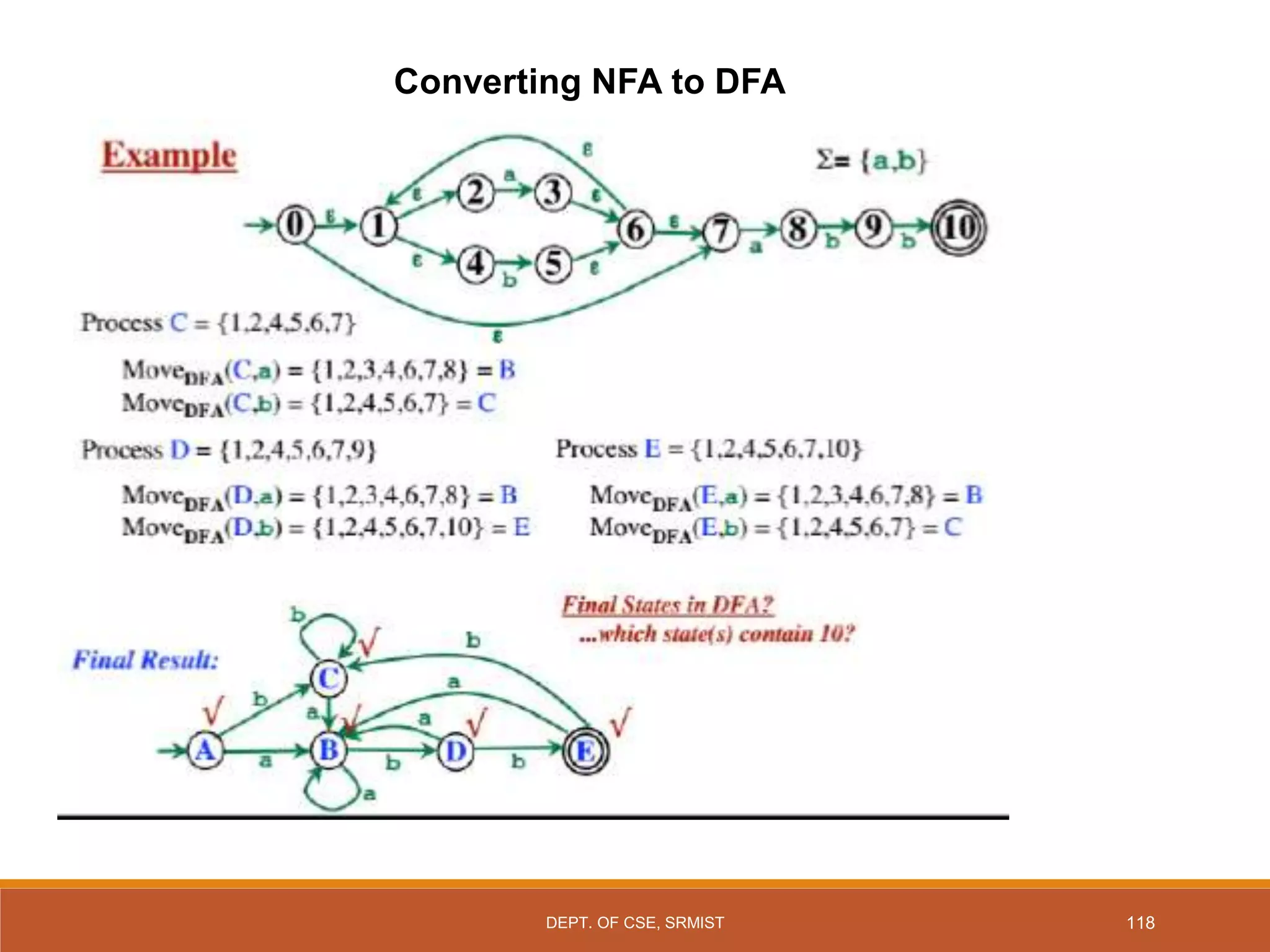
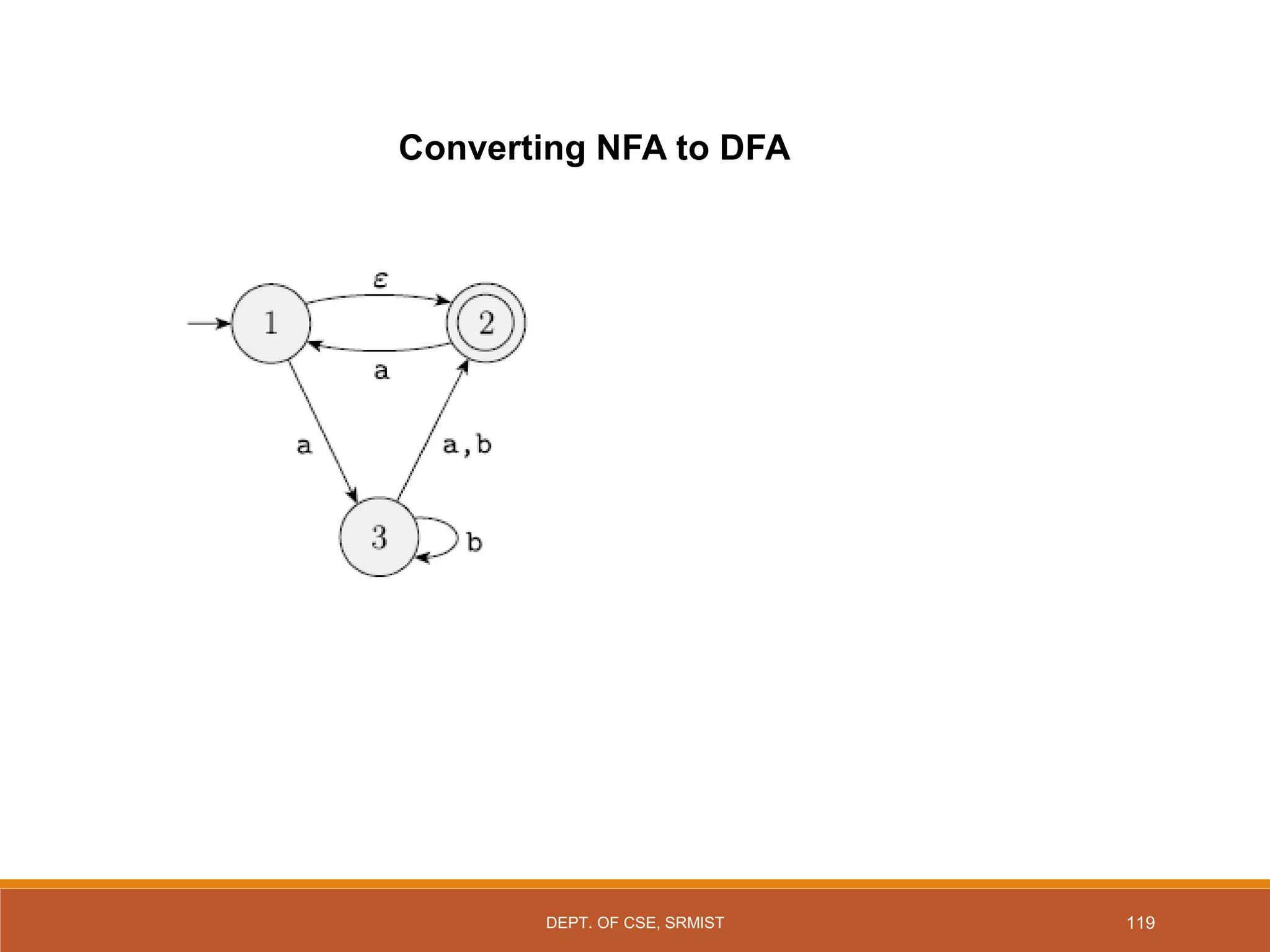
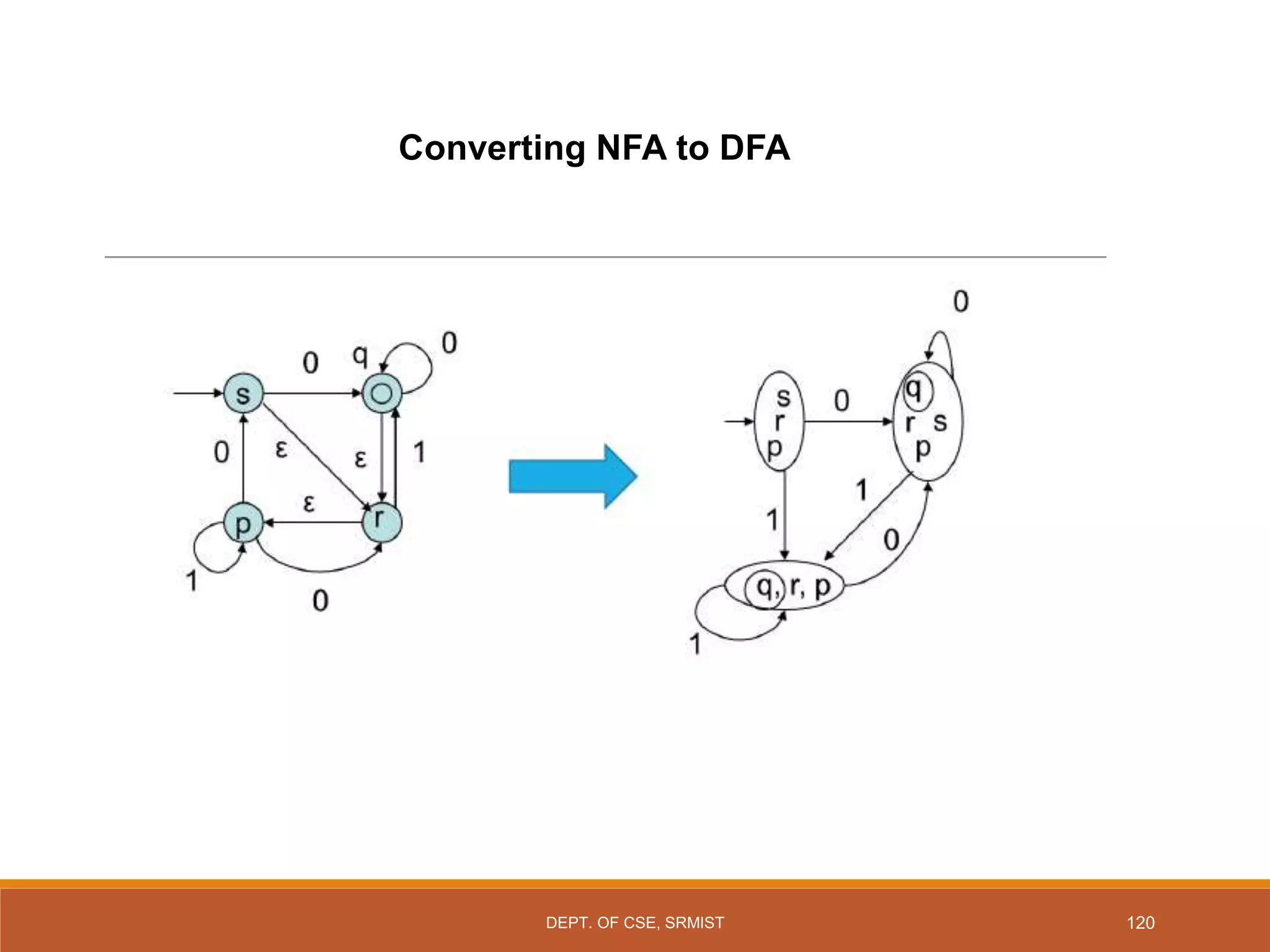
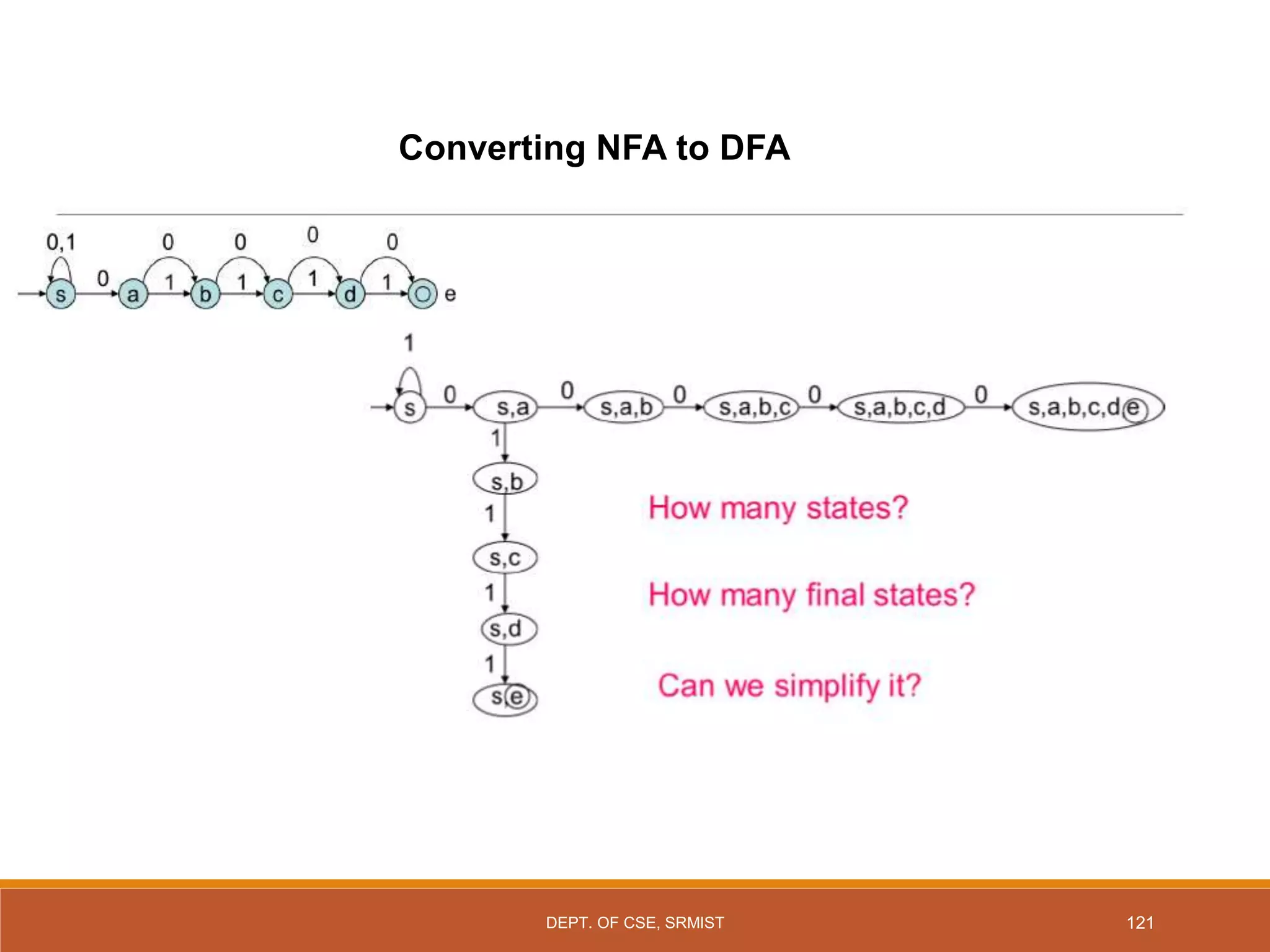
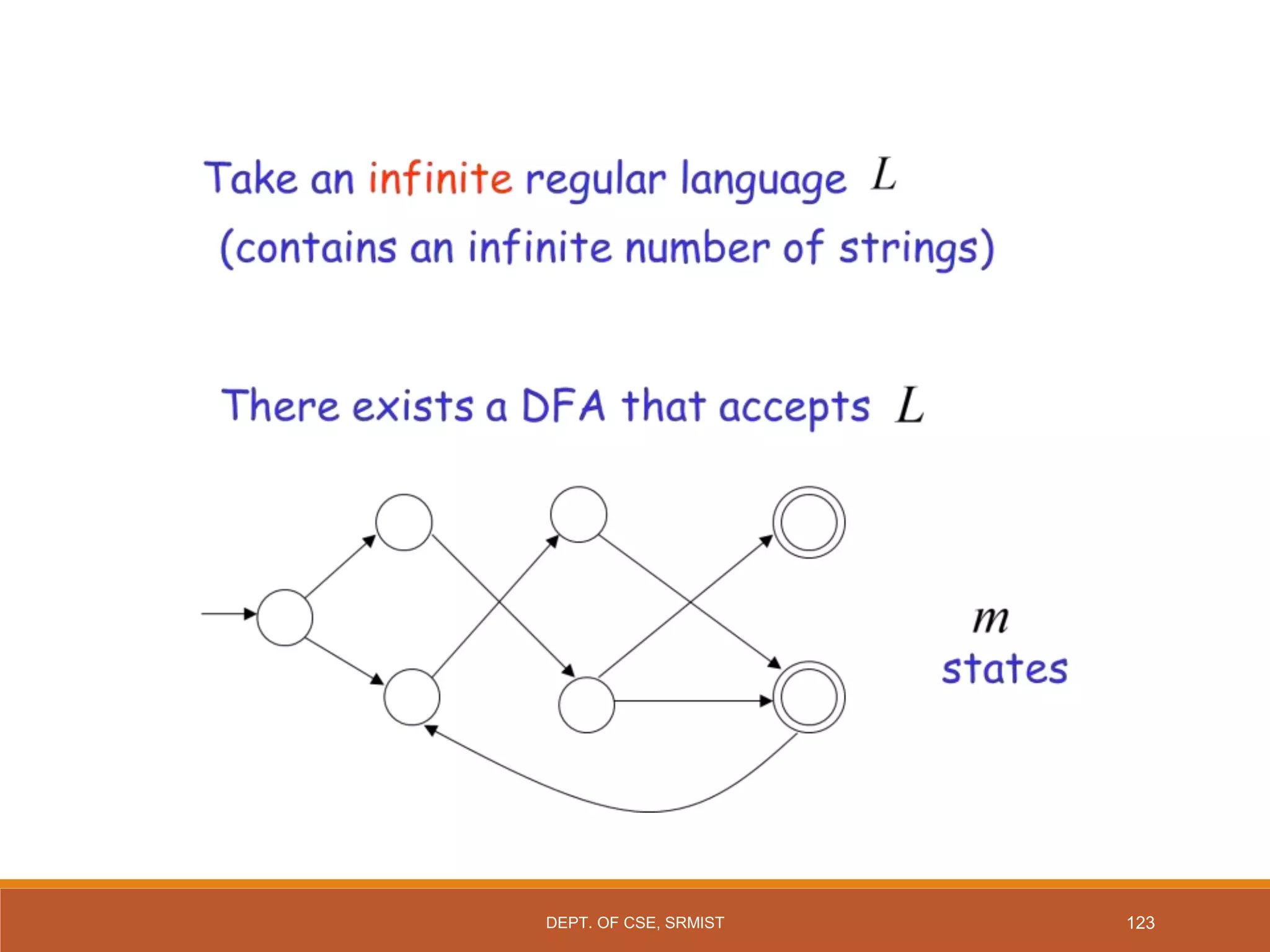
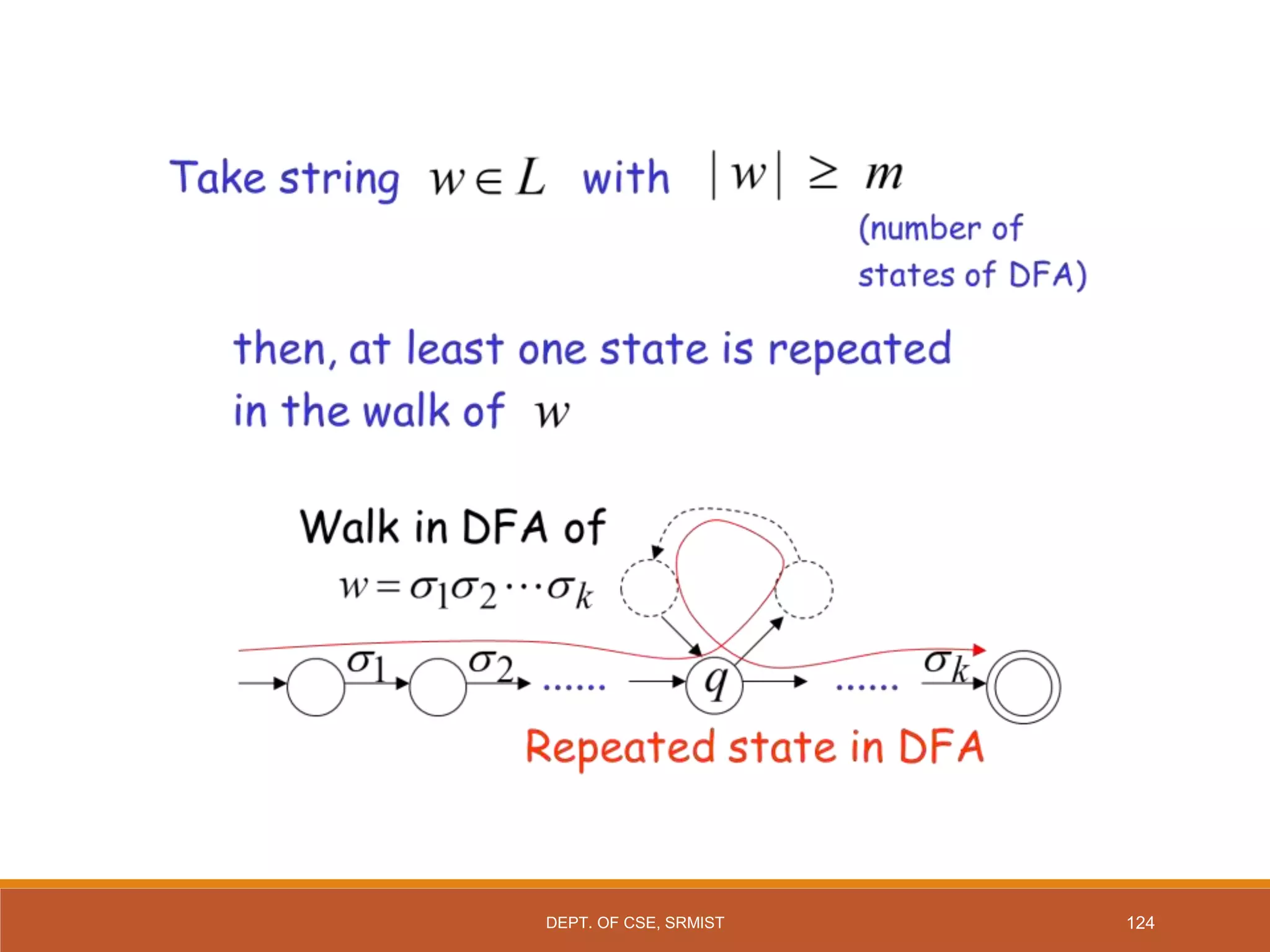
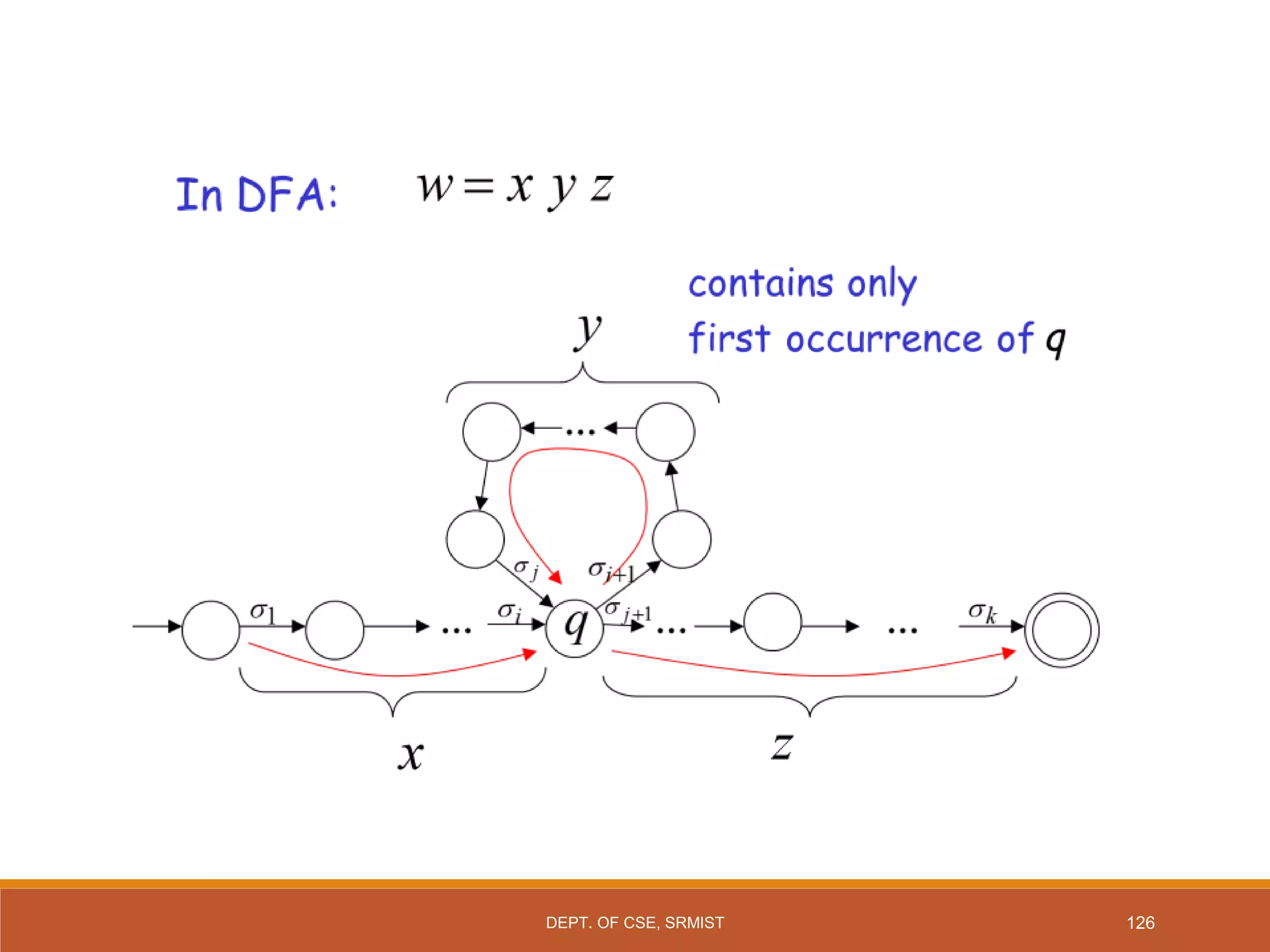
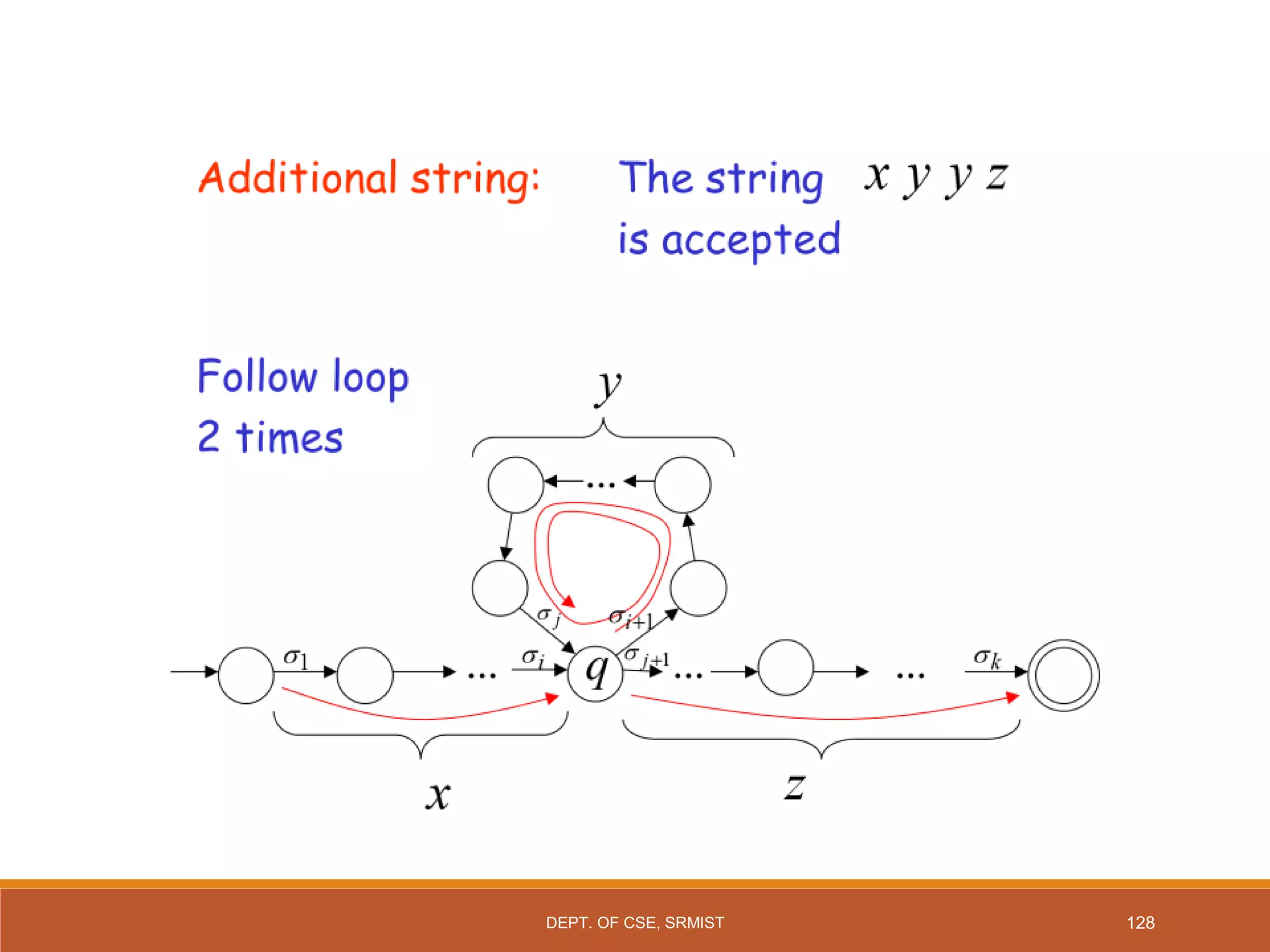
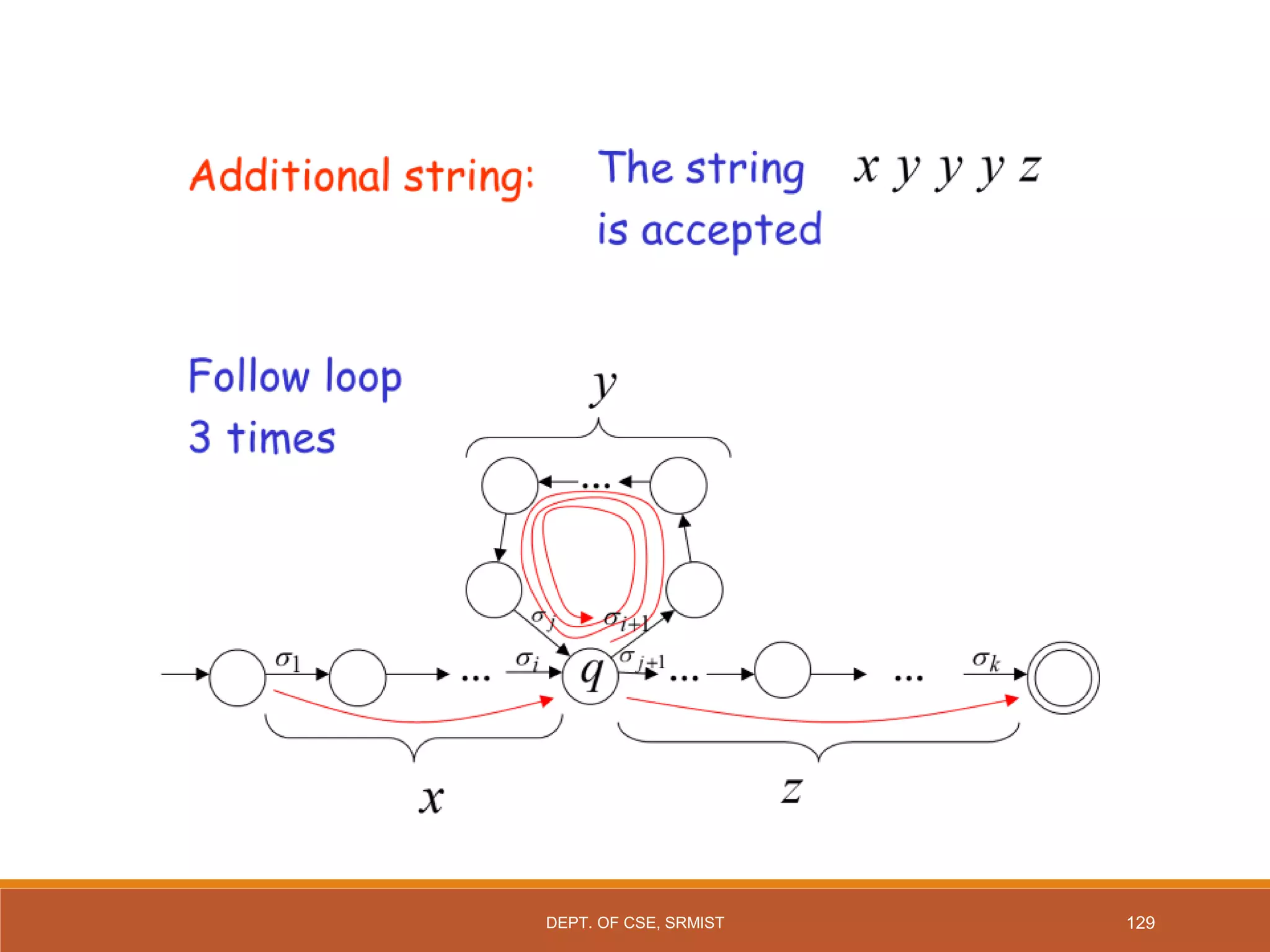
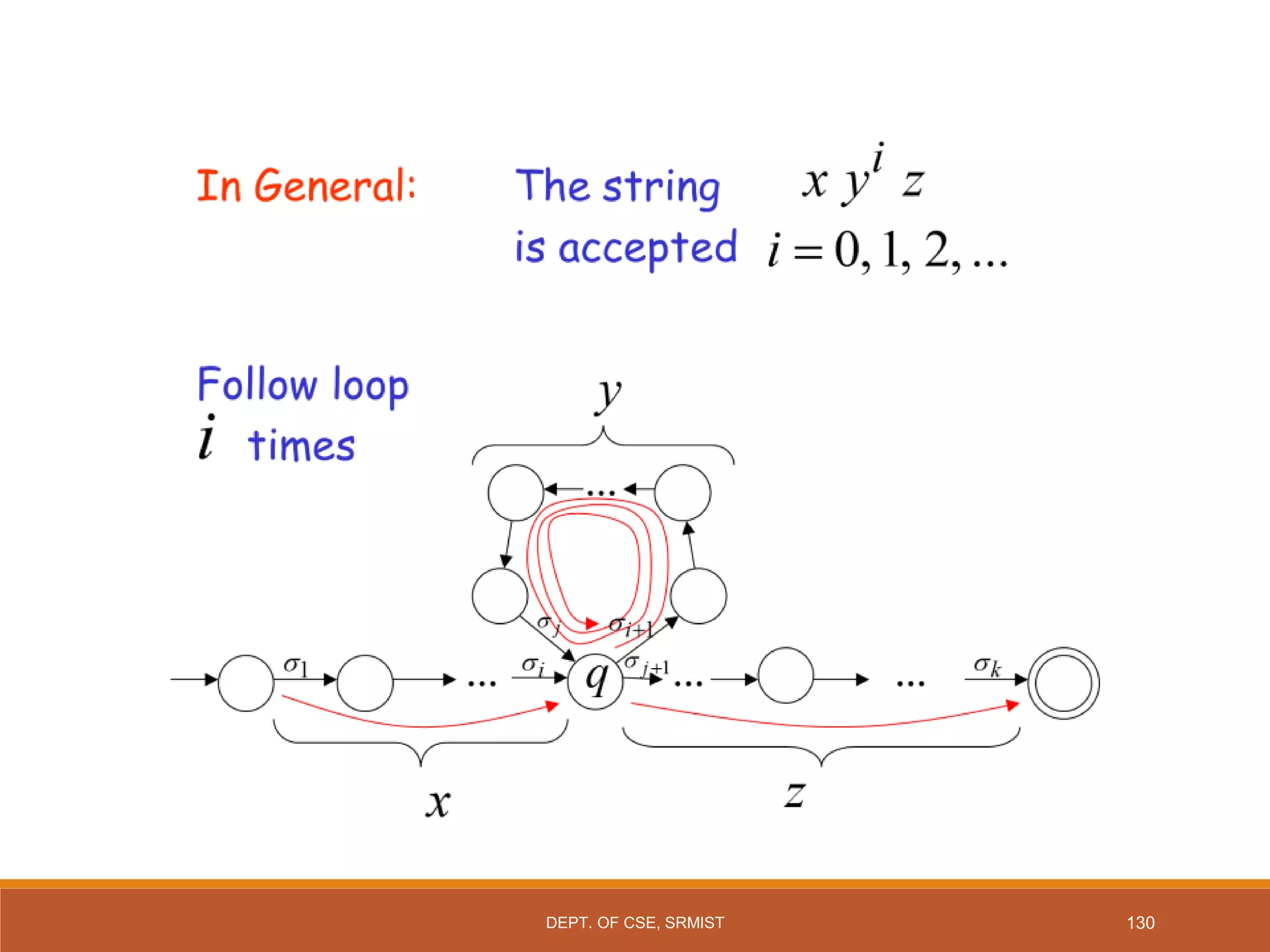
The document provides an overview of unit 1 of an introduction to automata course. It covers topics such as mathematical concepts for proofs including induction and deduction, formal languages involving strings and regular expressions, different types of finite automata including deterministic finite automata (DFAs) and nondeterministic finite automata, epsilon moves in finite automata, minimization of DFAs, properties of regular languages, and variants of finite automata. It also provides examples and problems related to many of these concepts.