This document discusses geometric routing in sensor networks and introduces an important open conjecture. It provides contributions towards bounding the failure of greedy routing and characterizing when it succeeds. Greedy routing works by recursively selecting the neighbor node closest to the destination but can fail when no such node exists, motivating the conjecture about when it is guaranteed to succeed.



![Introduction Conjecture Contribution Bound Characterization Geometric routing Greedy routing Greedy routing fails! Rubber band
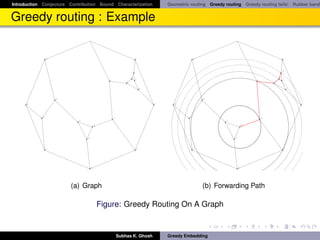
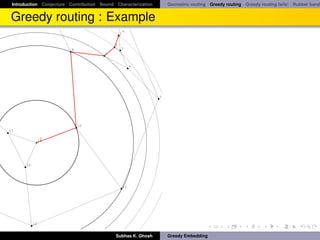
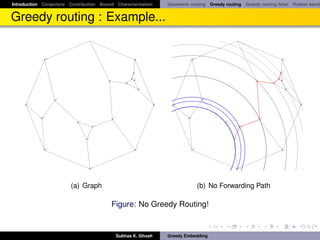
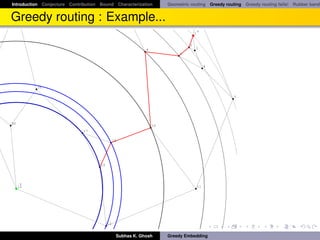
Greedy routing sometimes fails!
Greedy routing sometimes fails to deliver a packet because of the
phenomenon of “voids” (nodes with no neighbor closer to the destination).
This is essentially reaching a local minimum with respect to the distance
functional defined by s, t -pair.
Alternative: face routing [KK00].
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-9-320.jpg)
![Introduction Conjecture Contribution Bound Characterization Geometric routing Greedy routing Greedy routing fails! Rubber band
Geometric routing is complicated
It is unlikely that future ad hoc networks can rely on the availability of
precise geographic coordinates (GPS is costly and does not work in all
situation).
Importantly, the precise coordinates may be disadvantageous as they do
not account for obstructions or other topological properties of the
network.
How to retain the benefits of geographic routing in the absence of location
information?
Rao, Papadimitriou, Shenker and Stoica (in [RPSS03]) defined a scalable
coordinate-based routing algorithm that does not rely on location information,
and thus can be used in a wide variety of ad hoc and sensor-nets
environments.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-10-320.jpg)
![Introduction Conjecture Contribution Bound Characterization Geometric routing Greedy routing Greedy routing fails! Rubber band
Virtual Coordinates
In [RPSS03] the nodes first decide on fictitious virtual coordinates in R2 , and
then apply greedy routing based on those. The coordinates are found by a
distributed version of the rubber band algorithm originally due to Tutte [Tut60].
Note that embedding in higher dimension requires storing more
information per node.
On the basis of extensive experimentation in [RPSS03] authors showed
that this approach makes greedy routing much more reliable (works
97.5% cases).
Kleinberg proved 100% success rate by assigning virtual coordinates in
the hyperbolic plane rather than the Euclidean plane.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-11-320.jpg)





![Introduction Conjecture Contribution Bound Characterization Geometric routing Greedy routing Greedy routing fails! Rubber band
Tutte Embedding
Every 3-connected planar graph has a convex embedding in the the Euclidean
plane (using Tutte’s rubber band algorithm [Tut60]).
Theorem
Let G = ({1, ·, n} , E) be a 3-connected, planar graph that has a face
(k + 1, . . . , n) for some k < n. Let pk+1 , . . . , pn be the vertices (in this order) of
a convex (n − k)-gon. Let w : E → R+ be an assignment of positive weights
to the internal edges. Then:
There are unique positions p1 , . . . , pk ∈ R2 for the interior vertices such
that all interior vertices are in equilibrium.
All internal faces of G are then realized as non-overlapping convex
polygons.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-18-320.jpg)

![Introduction Conjecture Contribution Bound Characterization Greedy Embedding Conjecture Conjecture - Details Known results
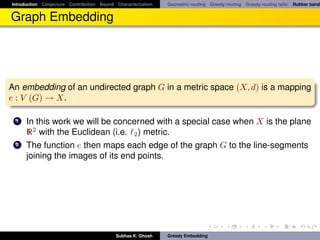
Greedy Embedding
Let d (pu , pv ) denote the Euclidean distance between two points pu and pv .
Definition
Greedy embedding ([PR05]): A greedy embedding x of a graph G = (V, E)
into a metric space (X, d) is a function x : V (G) → X with the following
property: for every pair of non-adjacent vertices s, t ∈ V (G) there exists a
vertex u ∈ V (G) adjacent to s such that d (x (u) , x (t)) < d (x (s) , x (t)).
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-21-320.jpg)
![Introduction Conjecture Contribution Bound Characterization Greedy Embedding Conjecture Conjecture - Details Known results
Greedy Embedding : Conjecture(Weak)
This notion of greedy embedding was defined by Papadimitriou and Ratajczak
in [PR05]. They have presented graphs which does not admit a greedy
embedding in the Euclidean plane, and conjectured following:
Conjecture
(Weak). Every 3-connected planar graph has a greedy embedding in the
Euclidean plane.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-22-320.jpg)
![Introduction Conjecture Contribution Bound Characterization Greedy Embedding Conjecture Conjecture - Details Known results
Greedy Embedding : Conjecture (Strong)
A convex embedding of a planar graph is a planar embedding with a property
that all faces, including the external faces are convex. Additionally,
Papadimitriou and Ratajczak stated the following stronger form of the
conjecture:
Conjecture
(Strong). Every 3-connected planar graph has a greedy convex embedding in
the Euclidean plane.
Note that every 3-connected planar graph has a convex embedding in the the
Euclidean plane (using Tutte’s rubber band algorithm [Tut60]).
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-23-320.jpg)


![Introduction Conjecture Contribution Bound Characterization Greedy Embedding Conjecture Conjecture - Details Known results
Known results
Recently, greedy embedding conjecture has been proved in [LM08]. In [LM08]
authors construct a greedy embedding into the Euclidean plane for all circuit
graphs – which is a generalization of 3-connected planar graphs. Similar
result was independently discovered by Angelini, Frati and Grilli [AFG08].
Theorem
([LM08]) Any 3-connected graph G without having a K3,3 minor admits a
greedy embedding into the Euclidean plane.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-27-320.jpg)
![Introduction Conjecture Contribution Bound Characterization Open Problem Weak greedy
Open Problem
The greedy embedding algorithm presented in [LM08, AFG08] not necessarily
produce a convex greedy embedding, and in fact the embedding may not
even be a planar one. In this work we consider the convex greedy embedding
conjecture. Other questions that we can ask:
1 What is the least dimension of a normed vector space V where every
graph with n nodes has a greedy embedding?
2 Why Tutte embedding improves delivery success?
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-28-320.jpg)
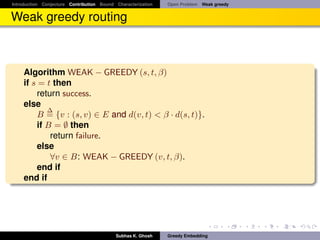
![Introduction Conjecture Contribution Bound Characterization Open Problem Weak greedy
Contribution
Given a 3-connected planar graph G = (V, E),
1 An embedding x : V → R2 of G is a planar convex greedy embedding if
and only if, in the embedding x, weight of the maximum weight spanning
tree (wt(T )) and weight of the minimum weight spanning tree (wt(MST))
1−δ
satisfies wt(T )/wt(MST) ≤ (|V | − 1) , for some 0 < δ ≤ 1.
√
2 G has a β-weak greedy convex embedding in R2 with β ∈ [1, 2 2 · d(G)].
Also, this bound is achieved by Tutte embedding.
3 We show a possibility that Tutte embedding with correct choice of edge
weights may produce greedy embedding of G.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-29-320.jpg)

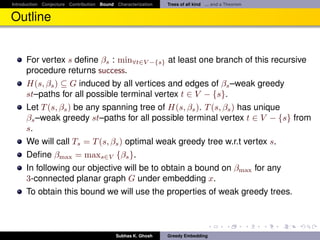







![Introduction Conjecture Contribution Bound Characterization Trees of all kind ... and a Theorem
Bounding the weight of trees: Outline...
It follows
Theorem
Let G = (V, E) be any three connected planar√graph. Then G has a β-weak
greedy convex embedding in R2 with β ∈ [1, 2 2 · d(G)]. Also, this bound is
achieved by Tutte embedding.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-40-320.jpg)
![Introduction Conjecture Contribution Bound Characterization Trees of all kind ... and a Theorem
However, this is not very good
F G F G
C
B C
B D
A D
A
E H E H
(a) (b)
Figure: Illustration of Tutte embedding of a cube: (a)Equal edge weights, (b)Unequal
edge weights
√
β ∈ [1, 2 2 · d(G)]
In Tutte embedding of a 3–connected planar graph G with arbitrary weights on
the edges, bound on β depends entirely on the choice of the edge weights in
the Tutte embedding.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-41-320.jpg)


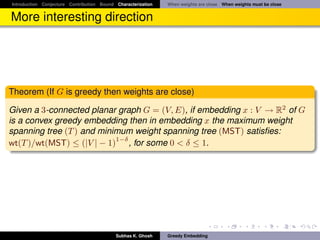
![Introduction Conjecture Contribution Bound Characterization When weights are close When weights must be close
Proof outline
Fact
A graph is 3-connected and planar if and only if each edge is in exactly two
non-separating induced cycles [Kel78]
1 Consider two cases: (Case - 1) e is on two internal faces F and F , and
(Case - 2) e is on the boundary face (infinite face is the other one).
2 Let us also assume that wt(T )/wt(MST) ≥ (|V | − 1). W.l.o.g. let
wt(MST) = 1. Since T is a spanning tree it has (|V | − 1) edges, and
hence has at least one edge e ∈ T of weight wt(e) ≥ 1.
Subhas K. Ghosh Greedy Embedding](https://image.slidesharecdn.com/greedyembeddingproblempresent-110919231235-phpapp02/85/Greedy-embedding-problem-45-320.jpg)