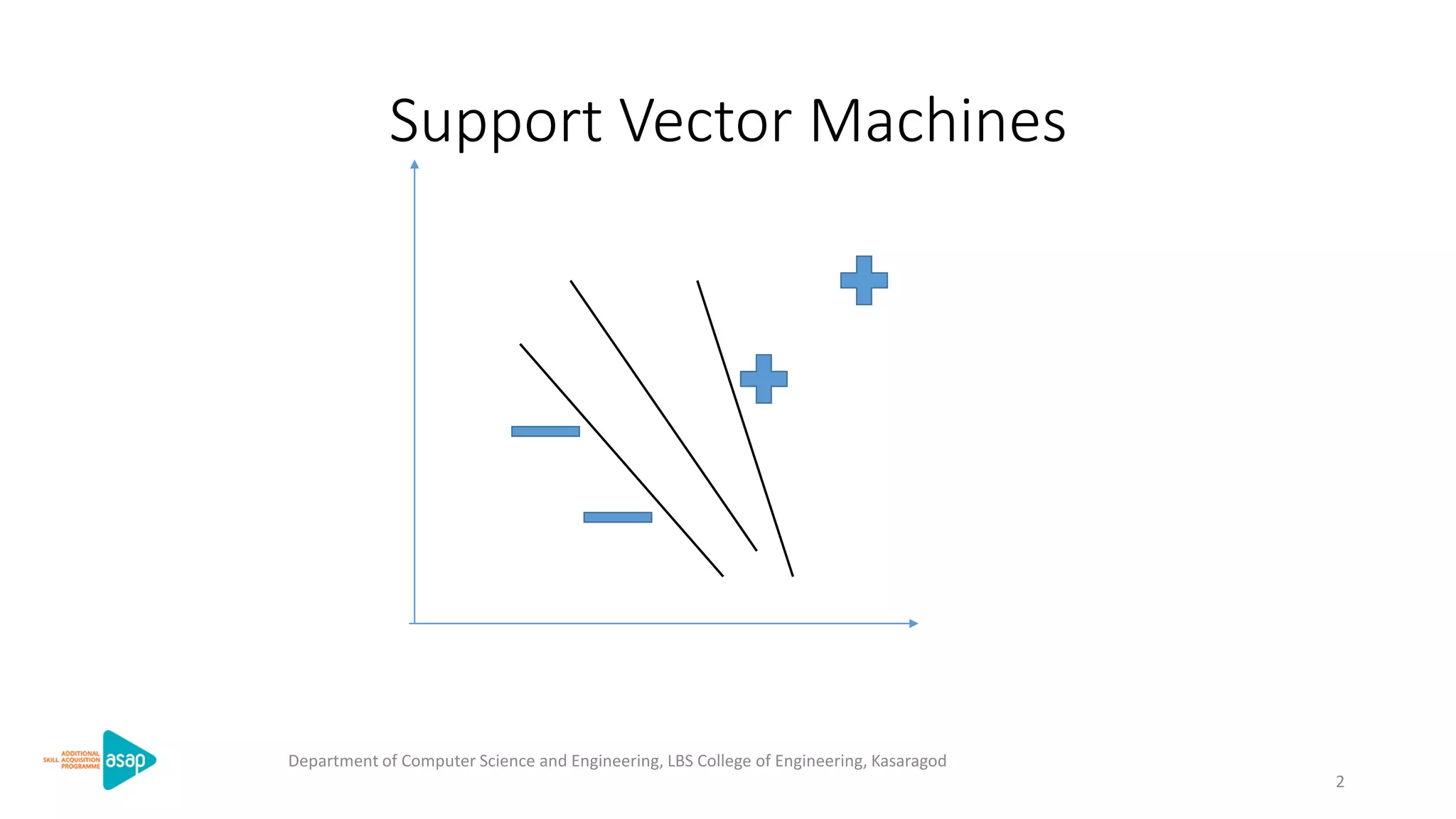
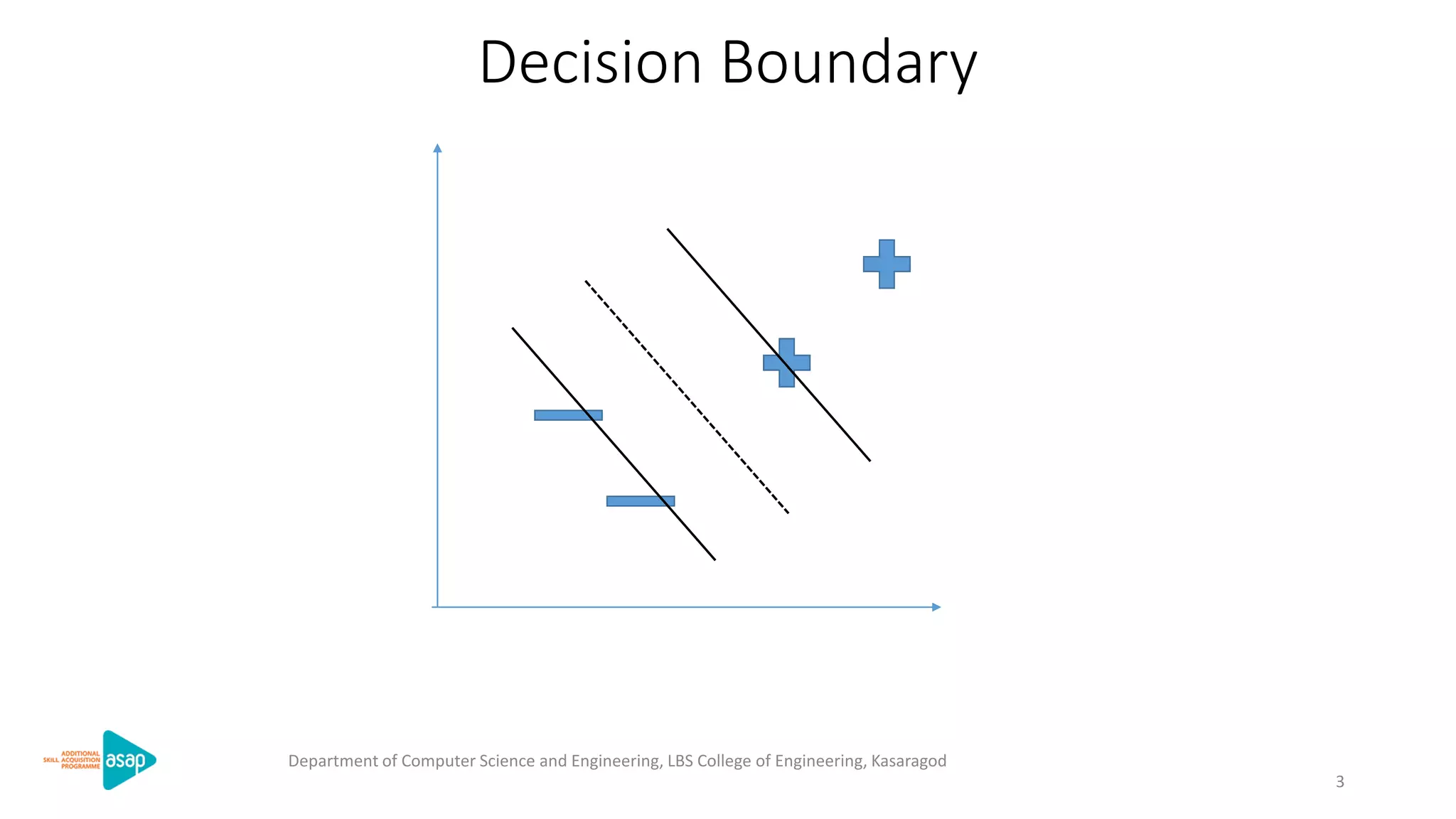
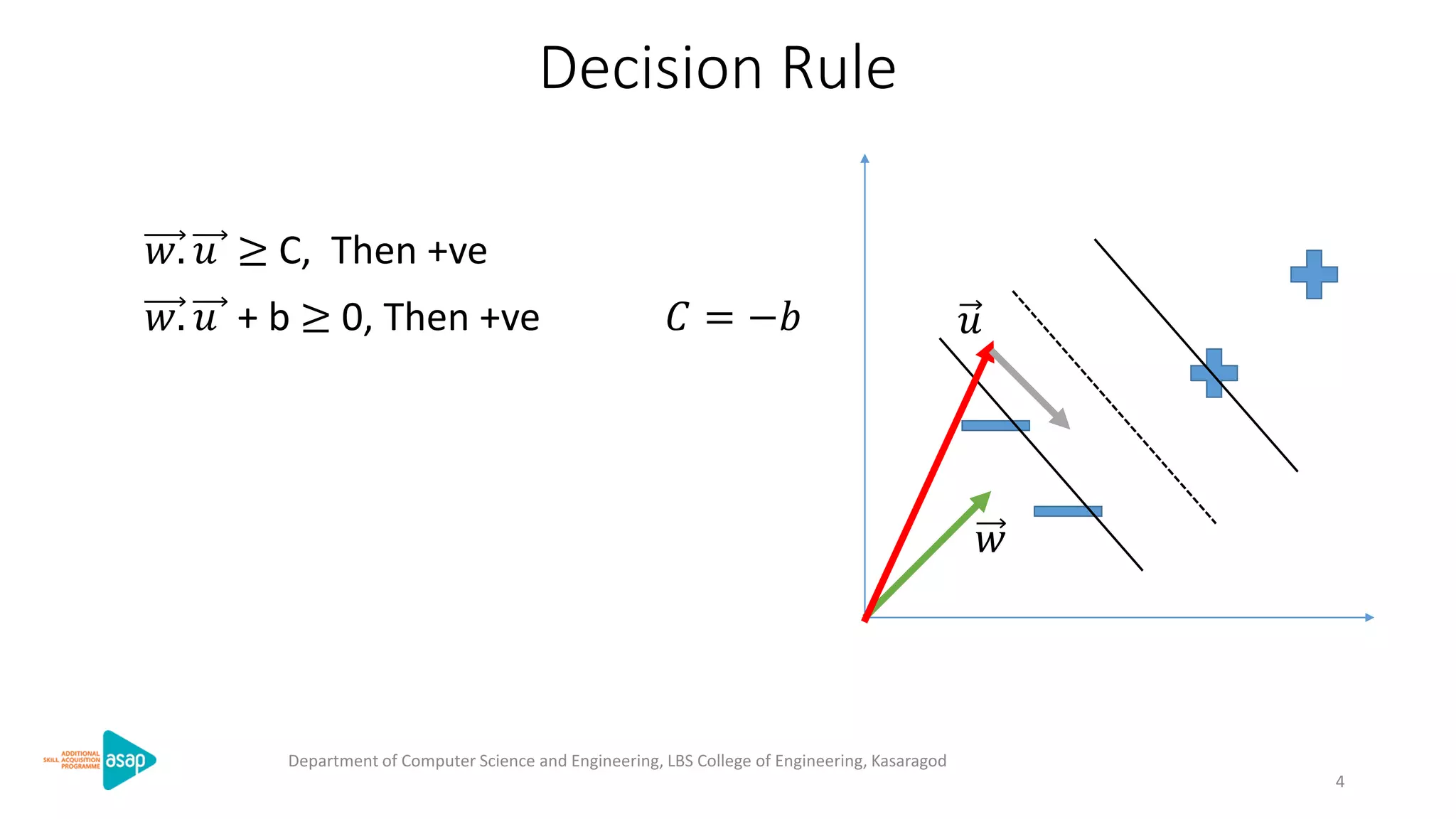
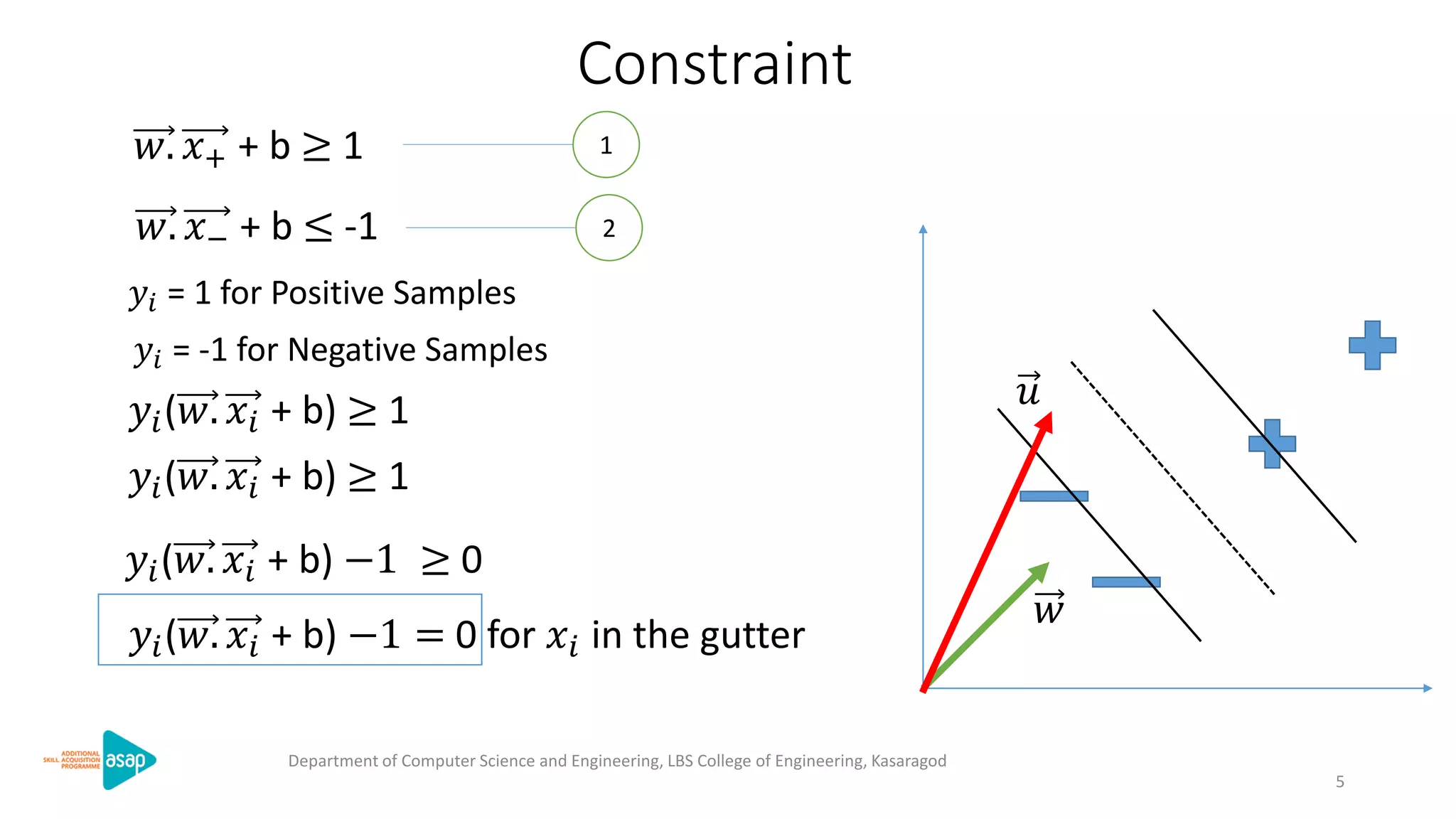
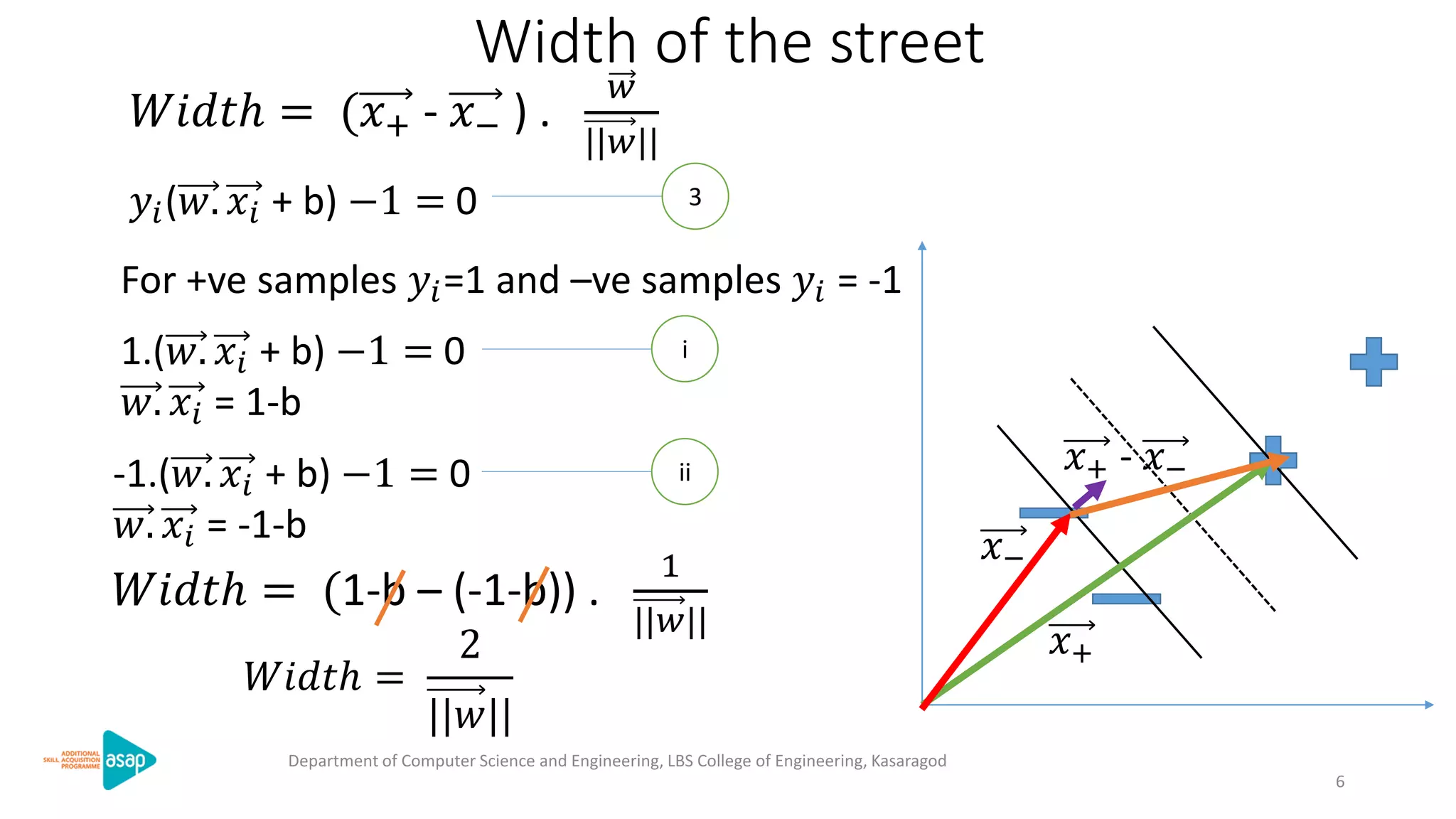
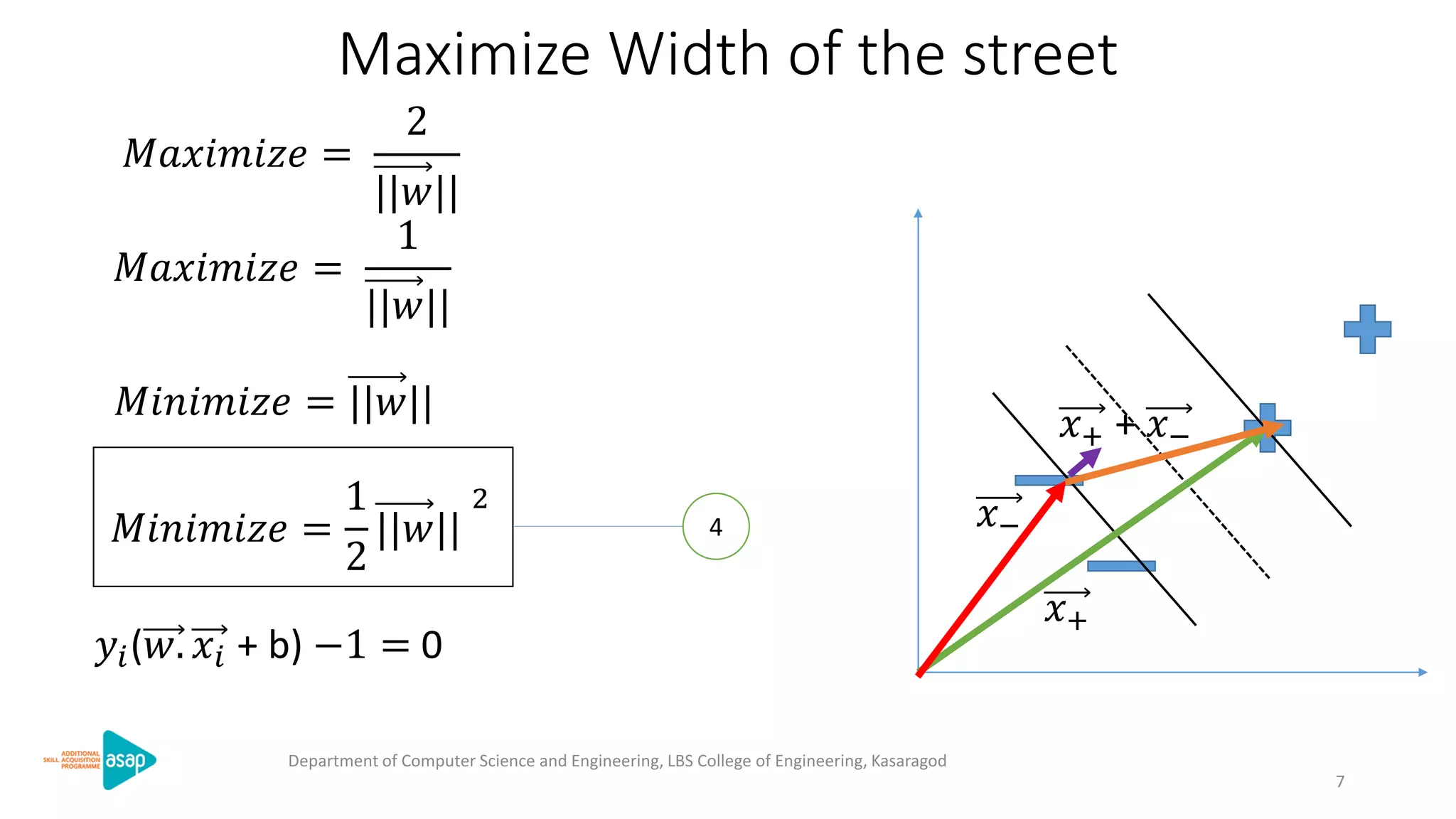
The document discusses support vector machines (SVMs), a supervised machine learning algorithm used for classification and regression. It describes how SVMs find the optimal separating hyperplane that maximizes the margin between the two classes of data points. The document provides the optimization formulation using Lagrange multipliers to find the separating hyperplane and defines the decision function to classify new data points. It also includes an example applying SVMs to classify a sample dataset.

1. SUPPORT VECTOR MACHINES
Sarith Divakar M
LBS College of Engineering, Kasaragod
sarith@lbscek.ac.in

2. Support Vector Machines
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
2

3. Decision Boundary
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
3

4. Decision Rule
𝑤
𝑢
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
4
𝑤. 𝑢 ≥ C, Then +ve
𝐶 = −𝑏𝑤. 𝑢 + b ≥ 0, Then +ve

5. Constraint
𝑤
𝑢
𝑤. 𝑥+ + b ≥ 1 1
𝑤. 𝑥− + b ≤ -1 2
𝑦𝑖(𝑤. 𝑥𝑖 + b) ≥ 1
𝑦𝑖 = 1 for Positive Samples
𝑦𝑖 = -1 for Negative Samples
𝑦𝑖(𝑤. 𝑥𝑖 + b) ≥ 1
𝑦𝑖(𝑤. 𝑥𝑖 + b) −1 ≥ 0
𝑦𝑖(𝑤. 𝑥𝑖 + b) −1 = 0 for 𝑥𝑖 in the gutter
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
5

6. Width of the street
𝑊𝑖𝑑𝑡ℎ = (𝑥+ - 𝑥− ) .
𝑤
||𝑤||
For +ve samples 𝑦𝑖=1 and –ve samples 𝑦𝑖 = -1
𝑦𝑖(𝑤. 𝑥𝑖 + b) −1 = 0 3
1.(𝑤. 𝑥𝑖 + b) −1 = 0
𝑤. 𝑥𝑖 = 1-b
i
-1.(𝑤. 𝑥𝑖 + b) −1 = 0
𝑤. 𝑥𝑖 = -1-b
ii
𝑊𝑖𝑑𝑡ℎ = (1-b – (-1-b)) .
1
||𝑤||
𝑥+
𝑥−
𝑥+ - 𝑥−
𝑊𝑖𝑑𝑡ℎ =
2
||𝑤||
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
6

7. Maximize Width of the street
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 =
2
||𝑤||
𝑥+
𝑥−
𝑥+ + 𝑥−
𝑀𝑎𝑥𝑖𝑚𝑖𝑧𝑒 =
1
||𝑤||
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 = ||𝑤||
𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 =
1
2
||𝑤||
2
4
𝑦𝑖(𝑤. 𝑥𝑖 + b) −1 = 0
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
7

8. Optimization using Lagrange multipliers
Expression: 𝑀𝑖𝑛𝑖𝑚𝑖𝑧𝑒 =
1
2
||𝑤||
2
Constraint: 𝑦𝑖(𝑤. 𝑥𝑖 + b) −1 = 0
L=
1
2
||𝑤||
2
- 𝛼𝑖 [𝑦𝑖(𝑤. 𝑥𝑖 + b) − 1]
𝜕𝐿
𝜕𝑤
= 𝑤- 𝛼𝑖 𝑦𝑖 𝑥𝑖 = 0
𝑤 = 𝛼𝑖 𝑦𝑖 𝑥𝑖 6
𝜕𝐿
𝜕𝑏
= - 𝛼𝑖 𝑦𝑖 = 0
𝛼𝑖 𝑦𝑖 = 0 7
5
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
8

9. Optimization using Lagrange multipliers
7
L=
1
2
||𝑤||
2
- 𝛼𝑖 [𝑦𝑖(𝑤. 𝑥𝑖 + b) − 1]
𝑤 = 𝛼𝑖 𝑦𝑖 𝑥𝑖
5
6
𝛼𝑖 𝑦𝑖 = 0
L=
1
2
( 𝛼𝑖 𝑦𝑖 𝑥𝑖 ).( 𝛼𝑗 𝑦𝑗 𝑥𝑗 )- 𝛼𝑖 [𝑦𝑖(( 𝛼𝑗 𝑦𝑗 𝑥𝑗 )𝑥𝑖 + b) − 1]
L=
1
2
( 𝛼𝑖 𝑦𝑖 𝑥𝑖 ).( 𝛼𝑗 𝑦𝑗 𝑥𝑗 )- ( 𝛼𝑖 𝑦𝑖 𝑥𝑖). ( 𝛼𝑗 𝑦𝑗 𝑥𝑗) − 𝛼𝑖 𝑦𝑖 b + 𝛼𝑖
= 0
L= 𝛼𝑖 +
1
2
( 𝛼𝑖 𝑦𝑖 𝑥𝑖 ).( 𝛼𝑗 𝑦𝑗 𝑥𝑗 )- ( 𝛼𝑖 𝑦𝑖 𝑥𝑖). ( 𝛼𝑗 𝑦𝑗 𝑥𝑗)
L= 𝛼𝑖 −
1
2
𝛼𝑖 𝑦𝑖 𝛼𝑗 𝑦𝑗 (𝑥𝑖. 𝑥𝑗)
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
9

10. Decision Rule
f(𝑢) = 𝛼𝑖 𝑦𝑖(𝑥𝑖 . 𝑢) - b
?
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
10

11. SVM Classifier
L= 𝛼𝑖
−
1
2
𝛼𝑖 𝑦𝑖 𝛼𝑗 𝑦𝑗 (𝑥𝑖. 𝑥𝑗)
Compute 𝑤 and b
Find vector 𝛼 which maximizes
Subject to
𝛼𝑖 𝑦𝑖 = 0
SVM Classifier Function:
𝑏 =
1
2
(𝑚𝑖𝑛𝑖:𝑦 𝑖=+1(𝑤. 𝑥𝑖) + 𝑚𝑎𝑥𝑖:𝑦 𝑖=−1(𝑤. 𝑥𝑖))
𝑤 = 𝛼𝑖 𝑦𝑖 𝑥𝑖
f( 𝑥) =(𝑤. 𝑥) - b
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
11

12. Solve following Question
1. Find the SVM classifier for the following dataset:
Sample F1 F2 Class
1 2 1 +1
2 4 3 -1
Question taken from Dr V N Krishnachandran, Vidya Centre for Artificial Intelligence Research, Vidya Academy of Science &
Technology, Thrissur
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod

13. 13
Sample F1 F2 Class
1 2 1 +1
2 4 3 -1
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
N = 2, 𝑥1 = (2,1), 𝑥2 = 4,3 ,𝑦1 = +1, 𝑦2 = −1
(𝛼1+𝛼2) −
1
2
[𝛼1 𝛼1 𝑦1 𝑦1(𝑥1. 𝑥1) + 𝛼1 𝛼2 𝑦1 𝑦2(𝑥1. 𝑥2) + 𝛼2 𝛼1 𝑦2 𝑦1(𝑥2. 𝑥1) + 𝛼2 𝛼2 𝑦2 𝑦2(𝑥2. 𝑥2) ]
(𝛼1+𝛼2) −
1
2
[𝛼1
2(+1)(+1)(2x2 + 1x1) + 𝛼1 𝛼2(+1)(-1)(2x4 + 1x3) + 𝛼2 𝛼1(-1) (+1)(4x2 + 3x1) +
𝛼2
2(-1)(-1)(4x4 + 3x3) ]
α1y1 + α2y2 =0 α1− α2 = 0
Find vector 𝛼 which maximizes 𝛼𝑖 −
1
2
𝛼𝑖 𝛼𝑗 𝑦𝑖 𝑦𝑗 (𝑥𝑖. 𝑥𝑗)
Subject to 𝛼𝑖 𝑦𝑖 = 0
α =(𝛼1, 𝛼2)
(𝛼1+𝛼2) −
1
2
[5𝛼1
2 -22𝛼1 𝛼2 + 25𝛼2
2 ]

14. 14
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
Find values of 𝛼1 and 𝛼2which maximizes ∅(α) = (𝛼1+𝛼2) −
1
2
[5𝛼1
2 -22𝛼1 𝛼2 + 25𝛼2
2 ]
Subject to conditions α1− α2 = 0, 𝛼1 > 0, 𝛼2 > 0
Substituting 2 in 1, ∅(α) = (𝛼1+𝛼1) −
1
2
[5𝛼1
2 -22𝛼1 𝛼1 + 25𝛼1
2 ]
2
1
= (2𝛼1) −
1
2
[8𝛼1
2 ]
2−8𝛼1 = 0For ∅(α) to be maximum
𝑑∅
𝑑𝛼1
= 0 𝛼1 = ¼ 𝛼2 = ¼
Second derivative is –ve so this is maximum
Sample F1 F2 Class
1 2 1 +1
2 4 3 -1

15. 15
Compute 𝑤 and b
𝑏 =
1
2
(𝑚𝑖𝑛𝑖:𝑦 𝑖=+1(𝑤. 𝑥𝑖) + 𝑚𝑎𝑥𝑖:𝑦 𝑖=−1(𝑤. 𝑥𝑖))𝑤 = 𝛼𝑖 𝑦𝑖 𝑥𝑖
𝑤 = 𝛼1 𝑦1 𝑥1 + 𝛼2 𝑦2 𝑥2
=
1
4
+1 2,1 +
1
4
(−1)(4,3)
=
1
4
[ 2,1 + −4, −3 ] =
1
4
[ −2, −2 ] = −
1
2
, −
1
2
𝑏 =
1
2
( (𝑤. 𝑥1) + (𝑤. 𝑥2))
=
1
2
( −
1
2
× 2 −
1
2
× 1 + (−
1
2
× 4 −
1
2
× 3))
Sample F1 F2 Class
1 2 1 +1
2 4 3 -1=
1
2
( −
3
2
+ (−
7
2
)) =
1
2
−
10
2
= −
5
2
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod

16. 16
SVM Classifier Function: f( 𝑥) =(𝑤. 𝑥) - b
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
= −
1
2
, −
1
2
. (𝑥1, 𝑥2) +
5
2
= −
1
2
𝑥1 −
1
2
𝑥2 +
5
2
= −
1
2
[𝑥1 + 𝑥2−5]
Equation of maximal margin line
f( 𝑥) = 0 𝑥1 + 𝑥2 = 5
0 1 2 3 4 5 6
1
2
3
4
5
6
Sampl
e
F1 F2 Class
1 2 1 +1
2 4 3 -1

17. Reference
1. Sudheep Elayidom, M. Data mining and warehousing, Cengage.
2. V. Vapnik, The Nature of Statistical Learning Theory, Springer, 1995
3. Vapnik, V. Statistical Learning Theory. John Wiley & Sons. Inc., New York, 1998
4. B. Schölkopf and A. J. Smola, Learning with Kernels, MIT Press, Cambridge, MA, 2002
5. Davide, M. and Simon, H. Advances in Kernel Methods, 1999, 226-227.
6. Jaiwei Han, Micheline Kamber, “Data Mining Concepts and Techniques”, Elsevier, 2006.
7. Pang-Ning Tan, Michael Steinbach, “Introduction to Data Mining”, Addison Wesley,
2006.
8. Dunham M H, “Data Mining: Introductory and Advanced Topics”, Pearson Education,
New Delhi, 2003.
9. Mehmed Kantardzic, “Data Mining Concepts, Methods and Algorithms”, John Wiley
and Sons, USA, 2003.
Department of Computer Science and Engineering, LBS College of Engineering, Kasaragod
17