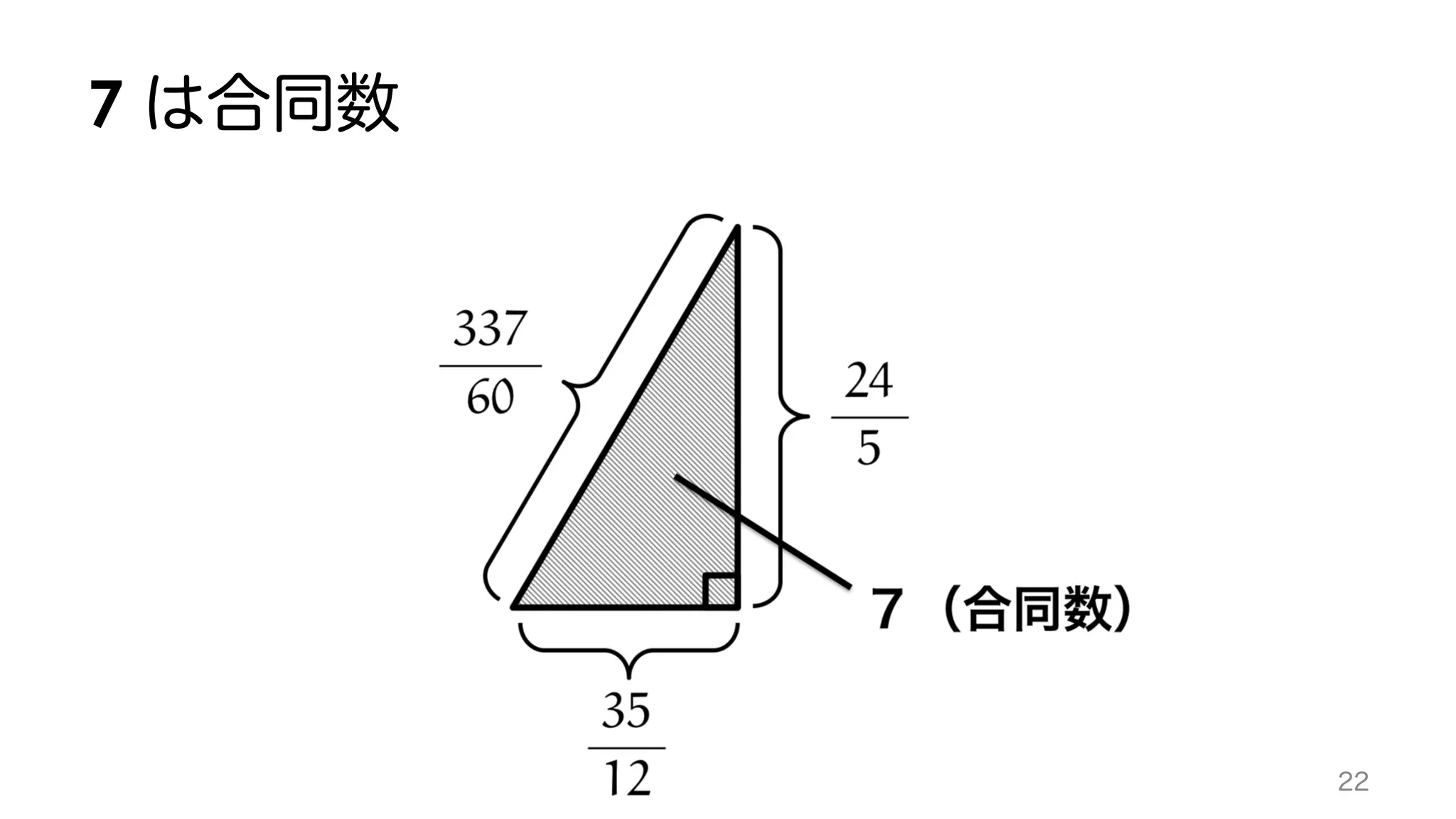
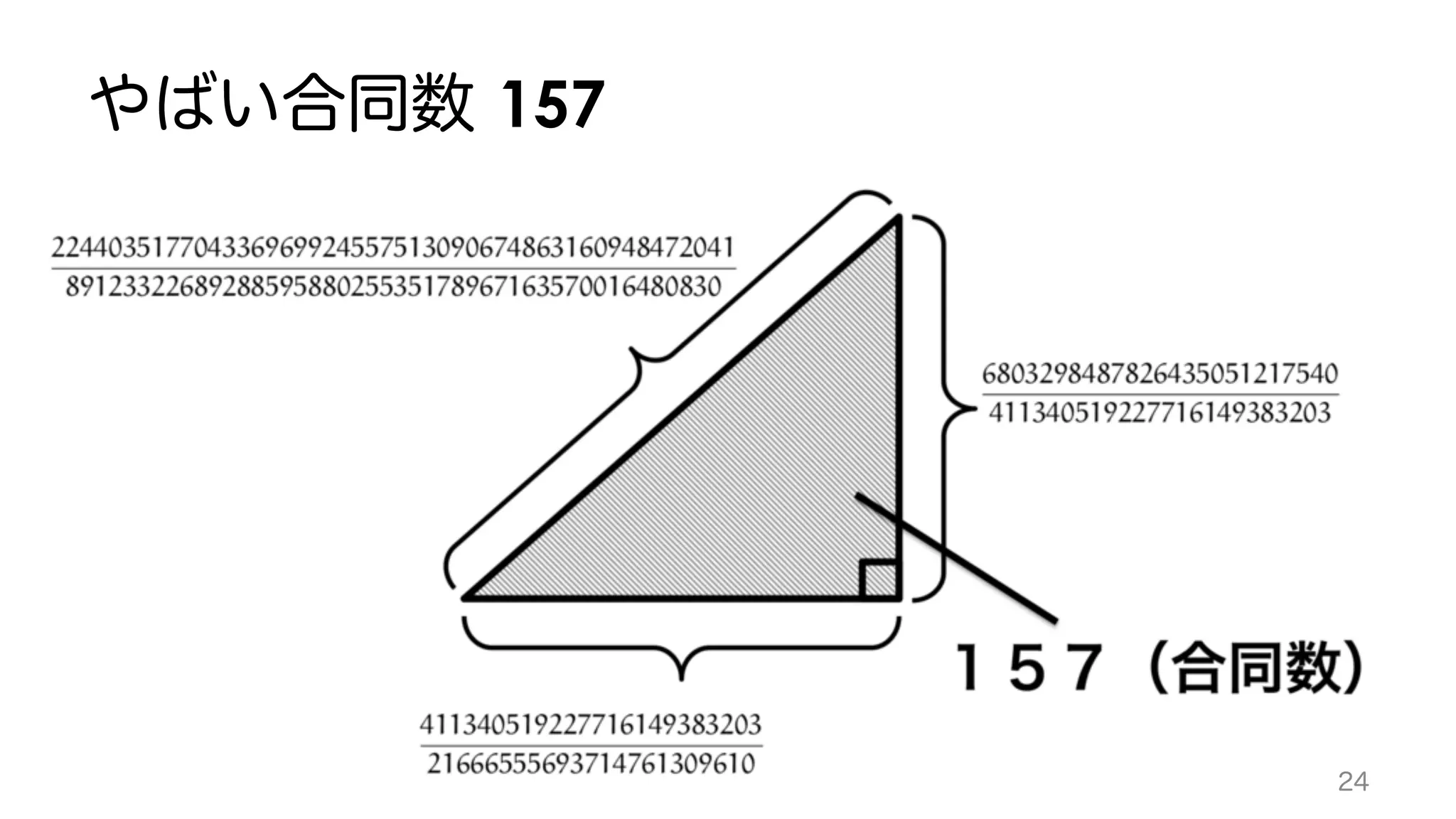
The document discusses various mathematical equations and theorems involving elliptic curves, specifically focusing on formulas related to ranks and L-functions. It mentions historical contributions from mathematicians like Waldspurger and highlights specific equations associated with integer representations. The equations are framed within the context of number theory and algebraic geometry.

1. @tsujimotter
2018/09/23 #
#{n = 2x2 + y2 + 32z2 } =
1
2
#{n = 2x2 + y2 + 8z2 }
L(En, 1) =
4
p
n
a2
n

3. 4
3
5
6

4. 5, 6, 7, 13, 14, 15, 20, 21, 22, 23, 24, 28, 29, 30, 31, 34, 37,
38, 39, 41, 45, 46, 47, …
1, 2, 3, 4, 8, 9, 10, 11, 12, 16, 17, 18, 19, 25, 26, 27, 32, 33,
35, 36, 40, 42, 43, 44, …

5. =) n
n
n = 2x2
+ y2
+ 8z2
n = 2x2
+ y2
+ 32z2
(x, y, z)
(x, y, z)
Thm. Tunnel (1983)
( )BSD
(=

7. n
X, Y, Z
8
<
:
X2
+ Y 2
= Z2
XY
2
= n
n ()

8. X2
+ Y 2
= Z2
(X Y )2
= Z2
4n (X + Y )2
= Z2
+ 4n
(X2
Y 2
)2
= Z4
42
n2
✓
(X2
Y 2
)Z
8
◆2
=
✓
Z
2
◆6
n2
✓
Z
2
◆2
⇥Z2
/26
x :=
✓
Z
2
◆2
y :=
✓
(X2
Y 2
)Z
8
◆2
±2XY = ±4n
y2
= x3
n2
x
XY = 2n

9. • n
• En
En : y2
= x3
n2
x
() En(Q)

10. BSD
E/Q : elliptic curve
rank E(Q) > 0 () ords=1 L(E, s) > 0
L(E, s) = 0
Thm. 1977
E/Q
rank E(Q) > 0 =) ords=1 L(E, s) > 0

11. n
() rank En(Q) > 0
BSD
=)
()()
L(En, 1) = 0

12. 1.
2.
3. Waldspurger

13. 1.
L(f, s) =
1X
n=1
bnn s
Mellin
Mellin
つ
Mellin
L(En, s) gEn 2 32n2
f(z) =
1X
n=1
bnqn

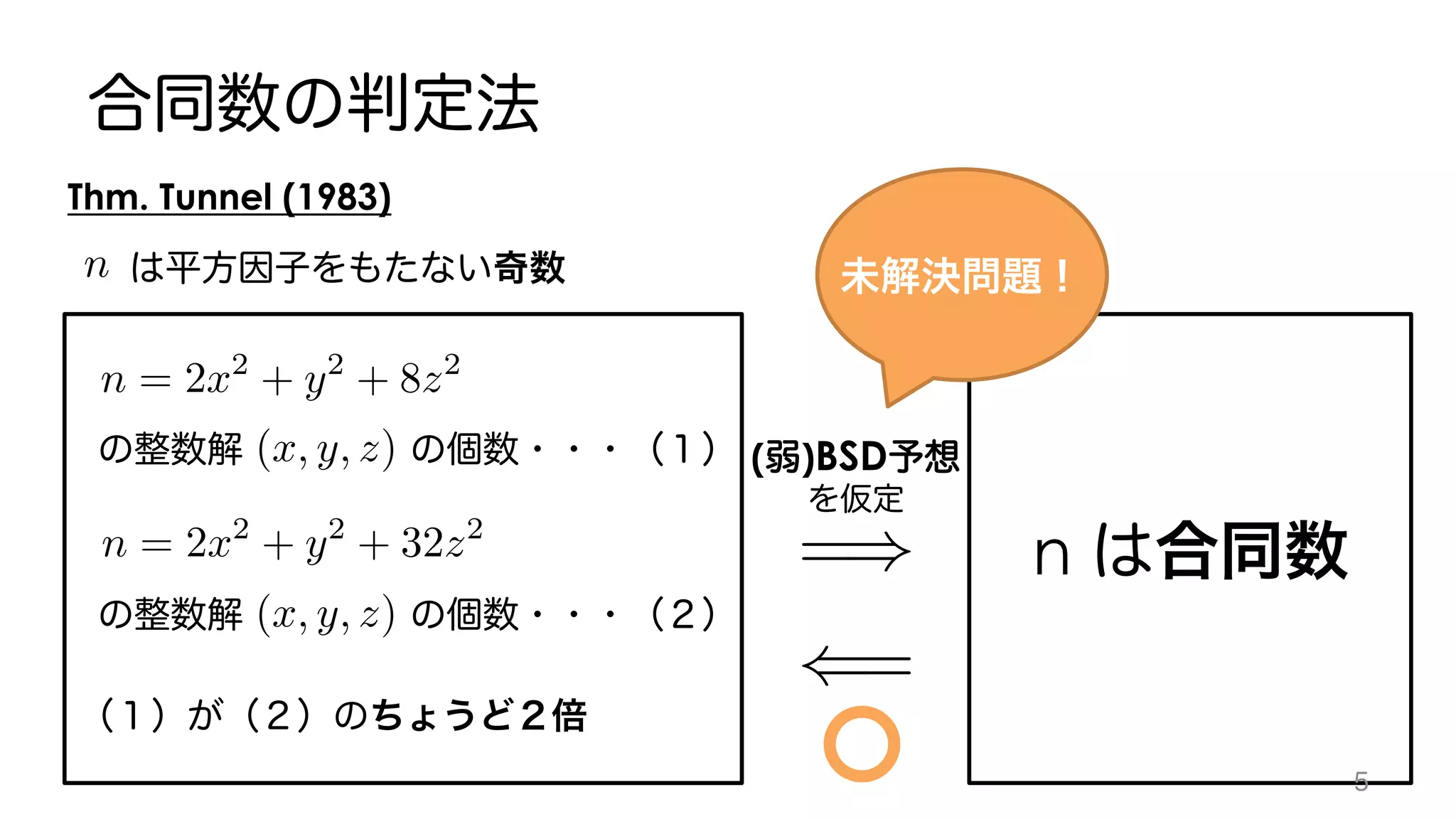
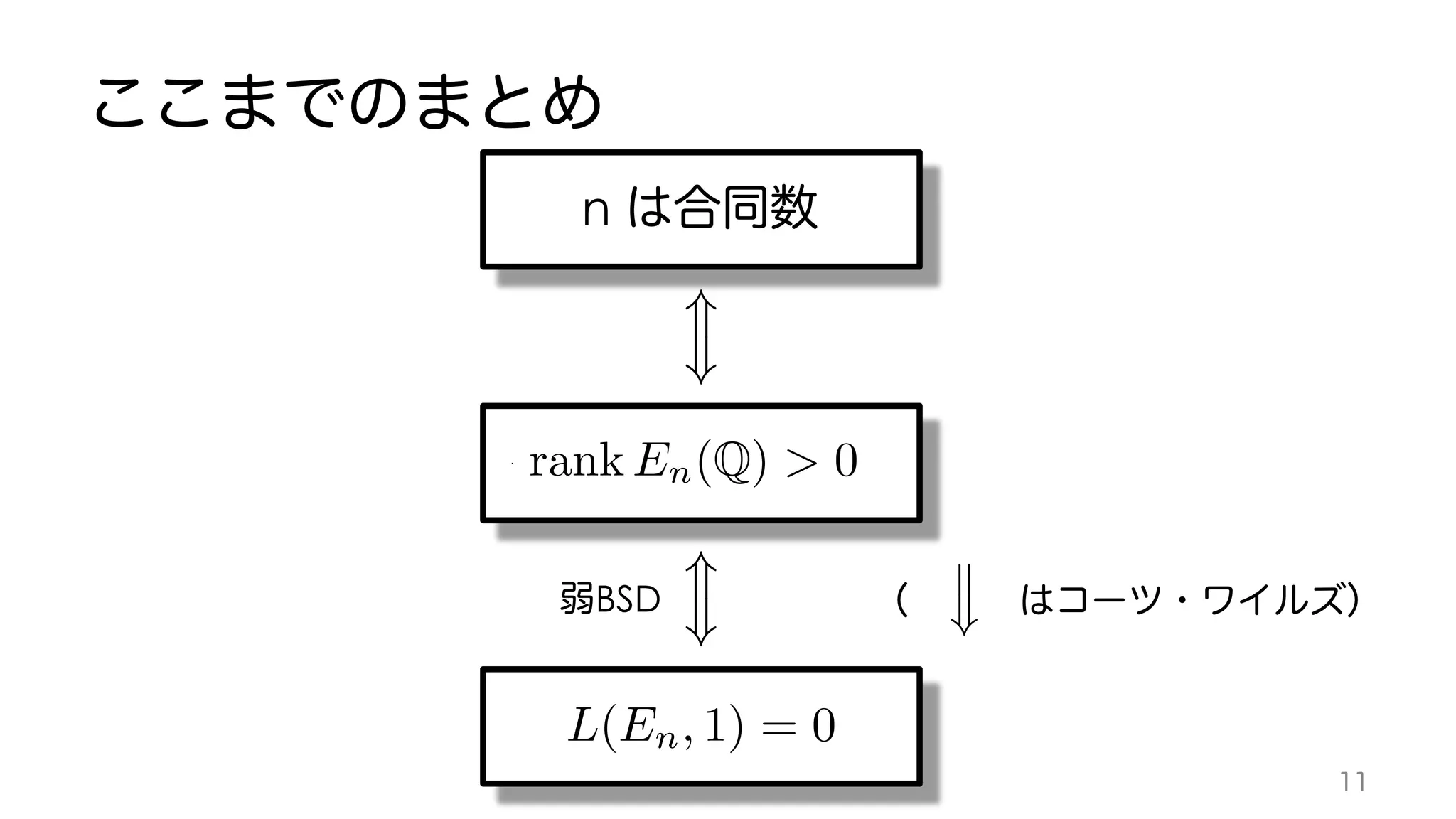
14. 2.
k/2 N k–1 N’
Sk/2(˜0(N), )
Shimura
! Mk 1(N0
, 2
)
N’ = N/2
Niwa 1975]
2 32
gE1 =
1X
m=1
bmqm
7 !
3/2 128
f =
1X
m=1
amqm

15. 3. Waldspurger
( , 1983)
n
f =
X
amqm
2 S3/2(˜0(128)) Shimura(f) = g =
X
bmqm
L(En, 1) =
4
p
n
a2
n L(En, 1) = 0 an = 0
(Waldspurger, 1980, 1981)
k–1 L
k/2 q- 2

16. f
q = e2⇡iz
Rem. 1/2
f(z) = (⇥(z) ⇥(4z))(⇥(32z)
1
2
⇥(8z))⇥(2z) 2 S3/2(˜0(128)
(8z))⇥(2z) 2 S3/2(˜0(128))
⇥(z) :=
X
n2Z
qn2

17. f(z) = (⇥(z) ⇥(4z))(⇥(32z)
1
2
⇥(8z))⇥(2z)
= ⇥(z)⇥(32z)⇥(2z)
1
2
⇥(z)⇥(8z)⇥(2z)
⇥(4z)⇥(32z)⇥(2z) +
1
2
⇥(4z)⇥(8z)⇥(2z)
=
X
x,y,z
q2x2
+y2
+32z2 1
2
X
x,y,z
q2x2
+y2
+8z2
X
x,y,z
q2x2
+4y2
+32z2
+
1
2
X
x,y,z
q2x2
+4y2
+8z2

18. an = #{n = 2x2
+ y2
+ 32z2
}
1
2
#{n = 2x2
+ y2
+ 8z2
}
#{n = 2x2
+ 4y2
+ 32z2
} +
1
2
#{n = 2x2
+ 4y2
+ 8z2
}
n : 0
() #{n = 2x2
+ y2
+ 32z2
} =
1
2
#{n = 2x2
+ y2
+ 8z2
}
an = 0

19. =) n
n
n = 2x2
+ y2
+ 8z2
n = 2x2
+ y2
+ 32z2
(x, y, z)
(x, y, z)
Thm. Tunnel (1983)
( )BSD
(=

20. N.
(2006)
– 1
– 3 3.3
– 4 4.4

22. 7

23. 7
✓
35
12
◆2
+
✓
24
5
◆2
=
30625 + 82944
3600
=
✓
337
60
◆2
1
2
·
35
12
·
24
5
= 7

24. 157

25. =)
n
n
(x, y, z)
(x, y, z)
Thm. Tunnel (1983)
( )BSD
n = 8x2
+ 2y2
+ 64z2
n = 8x2
+ 2y2
+ 16z2
=)