JaeJun Yoo, profile picture
Uploaded byJaeJun Yoo
PDF, PPTX2,055 views

Super resolution in deep learning era - Jaejun Yoo

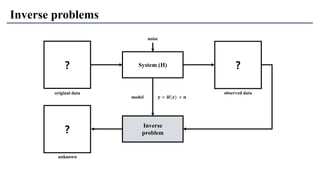
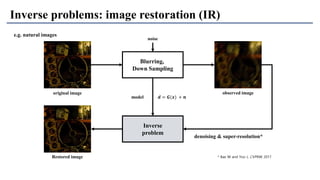
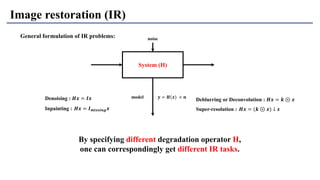
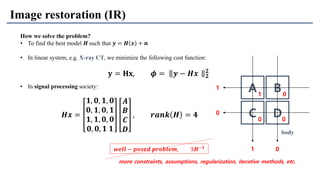
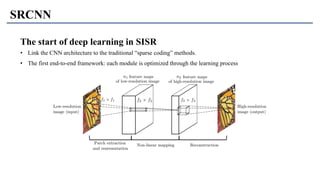
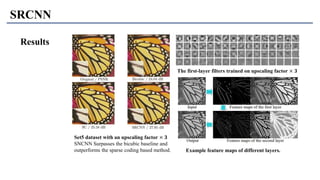
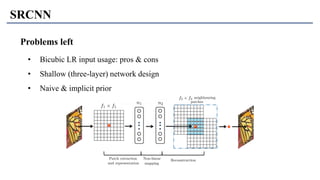
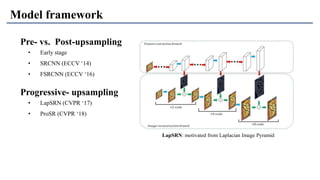
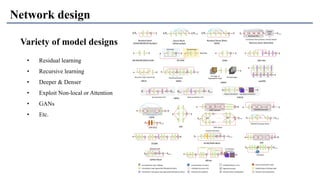
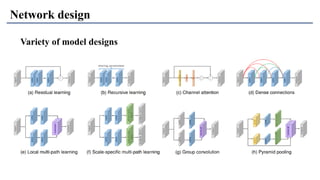
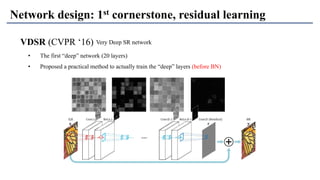
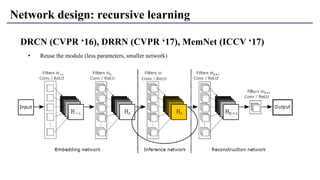
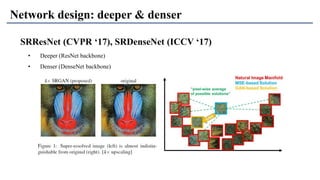
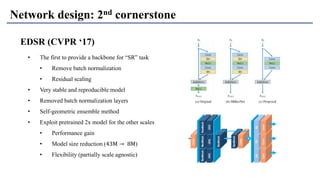
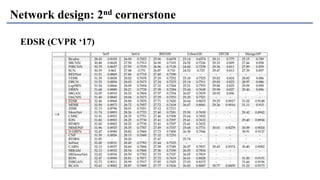
1) The document discusses super-resolution techniques in deep learning, including inverse problems, image restoration problems, and different deep learning models. 2) Early models like SRCNN used convolutional networks for super-resolution but were shallow, while later models incorporated residual learning (VDSR), recursive learning (DRCN), and became very deep and dense (SRResNet). 3) Key developments included EDSR which provided a strong backbone model and GAN-based approaches like SRGAN which aimed to generate more realistic textures but require new evaluation metrics.

Technology◦
Related topics:
image-enhancement•

Embed presentation

Download as PDF, PPTX
Super-resolution in deep learning era Jaejun Yoo Ph.D. AI Scientist @NAVER Clova AI Seminar, Math Dept., KAIST
System (H) noise Inverse problem unknown original data model 𝒚 = 𝑯(𝒙) + 𝒏 observed data ? ? ? Inverse problems
Inverse problems: scattering Maxwell equation Láme equation noise Inverse problem Restored density original density model 𝒚 = 𝑯(𝒙) + 𝒏 * Yoo J et al., SIAM, 2016 observed field e.g. electromagnetic, or acoustic wave physical property reconstruction* or source localization
Blurring, Down Sampling noise Inverse problem Restored image original image model 𝒅 = 𝑮(𝒙) + 𝒏 * Bae W and Yoo J, CVPRW, 2017 observed image e.g. natural images denoising & super-resolution* Inverse problems: image restoration (IR)
System (H) noise model 𝒚 = 𝑯(𝒙) + 𝒏 Image restoration (IR) By specifying different degradation operator H, one can correspondingly get different IR tasks. Deblurring or Deconvolution : 𝑯𝒙 = 𝒌 ⊛ 𝒙 Super-resolution : 𝑯𝒙 = (𝒌 ⊛ 𝒙) ↓ 𝒔 Denoising : 𝑯𝒙 = 𝑰𝒙 Inpainting : 𝑯𝒙 = 𝑰 𝒎𝒊𝒔𝒔𝒊𝒏𝒈 𝒙 General formulation of IR problems:
Given a single image 𝒚, solve f𝐨𝐫 𝒙: • 𝒚: known low resolution (LR) image • 𝒙: unknown high resolution (HR) image • 𝒌: unknown blur kernel (typically set as identity) • ↓ 𝒔: downsample 𝒙 by the factor of 𝒔 (typically done by bicubic function) • 𝒏: additive white Gaussian noise (AWGN) Single Image Super-Resolution 𝒚 = 𝒌 ⊛ 𝒙 ↓ 𝒔 + 𝒏
Image restoration (IR) 𝑯𝒙 = 𝟏, 𝟎, 𝟏, 𝟎 𝟎, 𝟏, 𝟎, 𝟏 𝟏, 𝟏, 𝟎, 𝟎 𝟎, 𝟎, 𝟏 𝟏 𝑨 𝑩 𝑪 𝑫 , 𝒓𝒂𝒏𝒌 𝑯 = 𝟒 A B DC 1 0 00 01 1 0 body 𝒘𝒆𝒍𝒍 − 𝒑𝒐𝒔𝒆𝒅 𝒑𝒓𝒐𝒃𝒍𝒆𝒎, ∃𝑯−𝟏 more constraints, assumptions, regularization, iterative methods, etc. How we solve the problem? • To find the best model 𝑯 such that 𝒚 = 𝑯 𝒙 + 𝒏 • In linear system, e.g. X-ray CT, we minimize the following cost function: • In signal processing society: 𝐲 = 𝐇𝐱, 𝝓 = 𝒚 − 𝑯𝒙 𝟐 𝟐
Image restoration (IR) From Bayesian perspective, the solution ෝ𝒙 can be obtained by solving a Maximum A Posteriori (MAP) problem: ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐚𝐱 𝒙 𝒍𝒐𝒈 𝒑 𝒚 𝒙 + 𝒍𝒐𝒈 𝒑(𝒙) ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) More formally, data fidelity regularization Enforces desired property of the output Guarantees the solution accords with the degradation process 1) Model-based optimization 2) Discriminative learning methods : What kinds of prior knowledge can we “impose on” our model?
Model-based optimization methods What kinds of prior knowledge can we “impose on” our model? • Sparsity • Wavelets, DCT, PCA, etc. • Dictionary learning • e.g., K-SVD • Nonlocal self-similarity • BM3D • Low-rankness ෝ𝜶 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝜶 𝟏 𝟐 𝒚 − 𝑯𝑫𝜶 𝟐 + 𝝀 𝜶 𝟏 ෡𝑿 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝑿 𝟏 𝟐 𝒀 − 𝑿 𝟐 + 𝝀 𝑿 ∗
Image restoration (IR) From Bayesian perspective, the solution ෝ𝒙 can be obtained by solving a Maximum A Posteriori (MAP) problem: ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐚𝐱 𝒙 𝒍𝒐𝒈 𝒑 𝒚 𝒙 + 𝒍𝒐𝒈 𝒑(𝒙) ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) More formally, data fidelity regularization Enforces desired property of the output Guarantees the solution accords with the degradation process 1) Model-based optimization 2) Discriminative learning methods What kinds of prior knowledge can we “learn using” our model? :
Discriminative learning methods What kinds of prior knowledge can we “learn using” our model? 𝐦𝐢𝐧 𝜽 𝒍 ෝ𝒙, 𝒙 , 𝒔. 𝒕. ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙; 𝜽) ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) data fidelity regularization Here, we learn the prior parameter 𝜽: through an optimization of a loss function 𝒍 on a training set (image pairs).
Discriminative learning methods CNNs (𝒇) 𝒚 𝒙 Conv, ReLU, pooling, etc. General statement of the problem: 𝐦𝐢𝐧 𝜽 𝒍 ෝ𝒙, 𝒙 , 𝒔. 𝒕. ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙; 𝜽) By replacing MAP inference with a predefined nonlinear function ෝ𝒙 = 𝒇 𝒚, 𝑯, 𝜽 , solving IR problem with CNNs can be treated as one of the discriminative learning methods. learn the image prior model
SRCNN The start of deep learning in SISR • Link the CNN architecture to the traditional “sparse coding” methods. • The first end-to-end framework: each module is optimized through the learning process
SRCNN Set5 dataset with an upscaling factor × 𝟑 SNCNN Surpasses the bicubic baseline and outperforms the sparse coding based method. The first-layer filters trained on upscaling factor × 𝟑 Example feature maps of different layers. Results
SRCNN Problems left • Bicubic LR input usage: pros & cons • Shallow (three-layer) network design • Naive & implicit prior
• Upsampling methods • Interpolation-based vs. Learning-based • Model framework • Pre-, Post-, Progressive- upsampling • Iterative up-and-down sampling • Network design • Residual learning • Recursive learning • Deeper & Denser • Etc. Developments of deep models in SISR
Pre- vs. Post-upsampling Progressive- upsampling Model framework LapSRN: motivated from Laplacian Image Pyramid • LapSRN (CVPR ‘17) • ProSR (CVPR ‘18) • Early stage • SRCNN (ECCV ‘14) • FSRCNN (ECCV ‘16)
Pre- vs. Post-upsampling Progressive- upsampling Iterative up-and-down sampling Model framework BPDN: motivated from iterative projection in the optimization methods. Super-resolution result on 8× enlargement. PSNR: LapSRN (15.25 dB), EDSR (15.33 dB), and BPDN (16.63 dB) • Deep Back-Projection Network (CVPR ‘18) • LapSRN (CVPR ‘17) • ProSR (CVPR ‘18) • Early stage • SRCNN (ECCV ‘14) • FSRCNN (ECCV ‘16)
Variety of model designs • Residual learning • Recursive learning • Deeper & Denser • Exploit Non-local or Attention • GANs • Etc. Network design
Variety of model designs Network design
VDSR (CVPR ‘16) Network design: 1st cornerstone, residual learning Very Deep SR network • The first “deep” network (20 layers) • Proposed a practical method to actually train the “deep” layers (before BN)
VDSR (CVPR ‘16) Network design: 1st cornerstone, residual learning Very Deep SR network • The first “deep” network (20 layers) • Proposed a practical method to actually train the “deep” layers
Network design: recursive learning DRCN (CVPR ‘16), DRRN (CVPR ‘17), MemNet (ICCV ‘17) • Reuse the module (less parameters, smaller network)
Network design: recursive learning DRCN (CVPR ‘16), DRRN (CVPR ‘17), MemNet (ICCV ‘17) • Reuse the module (less parameters, smaller network)
Network design: deeper & denser SRResNet (CVPR ‘17), SRDenseNet (ICCV ‘17) • Deeper (ResNet backbone) • Denser (DenseNet backbone)
Network design: deeper & denser SRResNet (CVPR ‘17), SRDenseNet (ICCV ‘17) • Deeper (ResNet backbone) • Denser (DenseNet backbone)
Network design: 2nd cornerstone EDSR (CVPR ‘17) • The first to provide a backbone for “SR” task • Remove batch normalization • Residual scaling • Very stable and reproducible model • Removed batch normalization layers • Self-geometric ensemble method • Exploit pretrained 2x model for the other scales • Performance gain • Model size reduction (43M → 8M) • Flexibility (partially scale agnostic)
Network design: 2nd cornerstone EDSR (CVPR ‘17)
Network design: 2nd cornerstone EDSR (CVPR ‘17)
Network design Non-local & Attention module Generative Adversarial Networks in Super-resolution • "Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network" (SRGAN, CVPR ‘17) • "A fully progressive approach to single-image super-resolution" (ProSR, CVPR ‘18) • "ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks" ECCV ‘18 • Candidate of 4th cornerstone? • "2018 PIRM Challenge on Perceptual Image Super-resolution" (ECCV ‘18) • 3rd cornerstone; at least in the perspective of the performance; too sensitive, many hyper-params. • "Image Super-Resolution Using Very Deep Residual Channel Attention Networks" (RCAN, ECCV ‘18) • "Non-local Recurrent Network for Image Restoration" (NLRN, NIPS ‘18) • "Residual Non-local Attention Networks for Image Restoration" (RNAN, ICLR ‘19)
GANs in SR: candidate of 4th cornerstone? Problems • Cannot go along with traditional metrics: PSNR / SSIM • New metric?; "2018 PIRM Challenge on Perceptual Image Super-resolution" (ECCV ‘18) ProSRGAN (CVPR ‘18)
Summary (until now) Methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) • Hand-crafted priors • Sparsity • Low-rankness • Learned discriminative priors • Predefined nonlinear function • CNNs 1) Model-based optimization 2) Discriminative learning methods
Pros General to handle different IR problems Clear physical meanings Data-driven end-to-end learning Efficient inference during test-phase Cons Hand-crafted priors (weak representations) Optimization task is time-consuming Generality of model is limited Interpretability of model is limited Summary (until now) Methods 1) Model-based optimization 2) Discriminative learning methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙)
Pros General to handle different IR problems Clear physical meanings Data-driven end-to-end learning Efficient inference during test-phase Cons Hand-crafted priors (weak representations) Optimization task is time-consuming Generality of model is limited Interpretability of model is limited Summary (until now) Methods 1) Model-based optimization 2) Discriminative learning methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) “Can we somehow get the best of both worlds?”
Getting the best of both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛
Getting the best of both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌)
Getting the best of both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 In Bayesian perspective, this is Gaussian denoising subproblem with noise level 𝝀/𝝁!𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌)
Getting the best of both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁)𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌)
Getting the best of both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁)𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌) 1. Any gray or color denoisers to solve a variety of inverse problems. 2. The explicit image prior can be unknown in solving the original equation. 3. Several complementary denoisers which exploit different image priors can be jointly utilized to solve one specific problem.
IRCNN HQS: Plug and Play • Image Restoration with CNN Denoiser Prior • Kai Zhang et al. “Learning Deep CNN Denoiser Prior for Image Restoration” 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁)
IRCNN HQS: Plug and Play • Image Restoration with CNN Denoiser Prior • Kai Zhang et al. “Learning Deep CNN Denoiser Prior for Image Restoration” 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁) Image deblurring performance comparison for Leaves image (the blur kernel is Gaussian kernel with standard deviation 1.6, the noise level σ is 2).
IRCNN HQS: Plug and Play • Image Restoration with CNN Denoiser Prior • Kai Zhang et al. “Learning Deep CNN Denoiser Prior for Image Restoration” 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁) SISR performance comparison for Set5: IRCNN can tune the blur kernel and scale factor w/o training. (the blur kernel is 7×7 Gaussian kernel with standard deviation 1.6, the scale factor × 3)
Pros General to handle different IR problems Clear physical meanings Data-driven end-to-end learning Efficient inference during test-phase Cons Hand-crafted priors (weak representations) Optimization task is time-consuming Generality of model is limited Interpretability of model is limited Summary (until now) Methods 1) Model-based optimization 2) Discriminative learning methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) √√
DPSR (CVPR ‘19) Deep Plug and Play Super-Resolution for Arbitrary Blur Kernels
Problems yet to be solved • It WORKS but NO WHYS. • Many studies are just blindly suggesting a new architecture that works. • Recent architecture are (kind of) overfitted to the dataset. • Bicubic downsampling tasks are saturated. (fails in other d/s scheme or realistic noises) • We need more “realistic” and “pragmatic” model that works in real environments. • Lack of fair comparisons • Lighter (greener) and faster (inference) models • New architectures (more than just a shared parameters) • New methods
Jaejun Yoo Ph.D. Research Scientist @NAVER Clova AI Research, South Korea Interested in Generative models, Signal Processing, Interpretable AI, and Algebraic Topology Techblog: https://jaejunyoo.blogspot.com Github: https://github.com/jaejun-yoo / LinkedIn: www.linkedin.com/in/jaejunyoo Research Keywords deep learning, inverse problem, signal processing, generative models Thank you Q&A?

More Related Content

PDF
Single Image Super Resolution Overview
byLEE HOSEONG
 
PPTX
A Deep Journey into Super-resolution
byRonak Mehta
 
PDF
Enhanced Deep Residual Networks for Single Image Super-Resolution
byNAVER Engineering
 
PDF
Generative adversarial networks
by남주 김
 
PPTX
Super resolution from a single image
byLakkhana Mallikarachchi
 
PDF
Finding connections among images using CycleGAN
byNAVER Engineering
 
PPTX
Tutorial on Object Detection (Faster R-CNN)
byHwa Pyung Kim
 
PPTX
Super Resolution
byalokahuti
 
Single Image Super Resolution Overview
byLEE HOSEONG
 
A Deep Journey into Super-resolution
byRonak Mehta
 
Enhanced Deep Residual Networks for Single Image Super-Resolution
byNAVER Engineering
 
Generative adversarial networks
by남주 김
 
Super resolution from a single image
byLakkhana Mallikarachchi
 
Finding connections among images using CycleGAN
byNAVER Engineering
 
Tutorial on Object Detection (Faster R-CNN)
byHwa Pyung Kim
 
Super Resolution
byalokahuti
 

What's hot

PDF
Convolutional neural network
byYan Xu
 
PPTX
You only look once (YOLO) : unified real time object detection
byEntrepreneur / Startup
 
PDF
Super resolution-review
byWoojin Jeong
 
PDF
Image-to-Image Translation with Conditional Adversarial Nets (UPC Reading Group)
byUniversitat Politècnica de Catalunya
 
PDF
Super resolution
byFederico D'Amato
 
PDF
Convolutional neural network
byItachi SK
 
PPTX
Recurrent Neural Network (RNN) | RNN LSTM Tutorial | Deep Learning Course | S...
bySimplilearn
 
PPTX
Deep learning for image super resolution
byPrudhvi Raj
 
PDF
Mobilenetv1 v2 slide
by威智 黃
 
PDF
Attention Models (D3L6 2017 UPC Deep Learning for Computer Vision)
byUniversitat Politècnica de Catalunya
 
PDF
PR-169: EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks
byJinwon Lee
 
PDF
MNIST and machine learning - presentation
bySteve Dias da Cruz
 
PPTX
Transformers in Vision: From Zero to Hero
byBill Liu
 
PPTX
Image super resolution
byAkshay Hazare
 
PDF
PR-409: Denoising Diffusion Probabilistic Models
byHyeongmin Lee
 
PDF
Transformer in Computer Vision
byDongmin Choi
 
PPTX
Recurrent Neural Network
byMohammad Sabouri
 
PPTX
Deep learning for object detection
byWenjing Chen
 
PPTX
Faster rcnn
by捷恩 蔡
 
PPTX
Mask R-CNN
byJaehyun Jun
 
Convolutional neural network
byYan Xu
 
You only look once (YOLO) : unified real time object detection
byEntrepreneur / Startup
 
Super resolution-review
byWoojin Jeong
 
Image-to-Image Translation with Conditional Adversarial Nets (UPC Reading Group)
byUniversitat Politècnica de Catalunya
 
Super resolution
byFederico D'Amato
 
Convolutional neural network
byItachi SK
 
Recurrent Neural Network (RNN) | RNN LSTM Tutorial | Deep Learning Course | S...
bySimplilearn
 
Deep learning for image super resolution
byPrudhvi Raj
 
Mobilenetv1 v2 slide
by威智 黃
 
Attention Models (D3L6 2017 UPC Deep Learning for Computer Vision)
byUniversitat Politècnica de Catalunya
 
PR-169: EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks
byJinwon Lee
 
MNIST and machine learning - presentation
bySteve Dias da Cruz
 
Transformers in Vision: From Zero to Hero
byBill Liu
 
Image super resolution
byAkshay Hazare
 
PR-409: Denoising Diffusion Probabilistic Models
byHyeongmin Lee
 
Transformer in Computer Vision
byDongmin Choi
 
Recurrent Neural Network
byMohammad Sabouri
 
Deep learning for object detection
byWenjing Chen
 
Faster rcnn
by捷恩 蔡
 
Mask R-CNN
byJaehyun Jun
 

Similar to Super resolution in deep learning era - Jaejun Yoo

PDF
[OSGeo-KR Tech Workshop] Deep Learning for Single Image Super-Resolution
byTaegyun Jeon
 
PPTX
Deep Learning for Search
byBhaskar Mitra
 
PDF
Ph.D. Thesis Presentation: A Study of Priors and Algorithms for Signal Recove...
byShunsuke Ono
 
PDF
MLIP - Chapter 6 - Generation, Super-Resolution, Style transfer
byCharles Deledalle
 
PPTX
Deep Learning for Search
byBhaskar Mitra
 
PDF
Multi-stage Progressive Image Restoration
bySonalShrin
 
PDF
Robustness in Deep Learning - Single Image Denoising using Untrained Networks...
byDaniel983829
 
PDF
Pixel Recursive Super Resolution. Google Brain
byeraser Juan José Calderón
 
PDF
An introduction to super resolution using deep learning
byAnil Chandra Naidu Matcha
 
PDF
Learning to Reconstruct
byJonas Adler
 
PDF
Image super resolution using Generative Adversarial Network.
byIRJET Journal
 
PDF
Low Complexity Regularization of Inverse Problems - Course #2 Recovery Guaran...
byGabriel Peyré
 
PDF
An adaptive-model-for-blind-image-restoration-using-bayesian-approach
byCemal Ardil
 
PPTX
A Fully Progressive approach to Single image super-resolution
byMohammed Ashour
 
PPTX
Thesis presentation
byJulián Tachella
 
PDF
Seminarpaper
byPrashantChaudhari75
 
PDF
deep CNN vs conventional ML
byChao Han chaohan@vt.edu
 
PDF
Analysis of Various Single Frame Super Resolution Techniques for better PSNR
byIRJET Journal
 
PPTX
Equivariant Imaging
byJulián Tachella
 
PDF
IRJET - Single Image Super Resolution using Machine Learning
byIRJET Journal
 
[OSGeo-KR Tech Workshop] Deep Learning for Single Image Super-Resolution
byTaegyun Jeon
 
Deep Learning for Search
byBhaskar Mitra
 
Ph.D. Thesis Presentation: A Study of Priors and Algorithms for Signal Recove...
byShunsuke Ono
 
MLIP - Chapter 6 - Generation, Super-Resolution, Style transfer
byCharles Deledalle
 
Deep Learning for Search
byBhaskar Mitra
 
Multi-stage Progressive Image Restoration
bySonalShrin
 
Robustness in Deep Learning - Single Image Denoising using Untrained Networks...
byDaniel983829
 
Pixel Recursive Super Resolution. Google Brain
byeraser Juan José Calderón
 
An introduction to super resolution using deep learning
byAnil Chandra Naidu Matcha
 
Learning to Reconstruct
byJonas Adler
 
Image super resolution using Generative Adversarial Network.
byIRJET Journal
 
Low Complexity Regularization of Inverse Problems - Course #2 Recovery Guaran...
byGabriel Peyré
 
An adaptive-model-for-blind-image-restoration-using-bayesian-approach
byCemal Ardil
 
A Fully Progressive approach to Single image super-resolution
byMohammed Ashour
 
Thesis presentation
byJulián Tachella
 
Seminarpaper
byPrashantChaudhari75
 
deep CNN vs conventional ML
byChao Han chaohan@vt.edu
 
Analysis of Various Single Frame Super Resolution Techniques for better PSNR
byIRJET Journal
 
Equivariant Imaging
byJulián Tachella
 
IRJET - Single Image Super Resolution using Machine Learning
byIRJET Journal
 

More from JaeJun Yoo

PDF
[PR12] categorical reparameterization with gumbel softmax
byJaeJun Yoo
 
PDF
A beginner's guide to Style Transfer and recent trends
byJaeJun Yoo
 
PPTX
[PR12] Inception and Xception - Jaejun Yoo
byJaeJun Yoo
 
PDF
Variants of GANs - Jaejun Yoo
byJaeJun Yoo
 
PDF
[PR12] PixelRNN- Jaejun Yoo
byJaeJun Yoo
 
PDF
[PR12] Capsule Networks - Jaejun Yoo
byJaeJun Yoo
 
PPTX
[Pr12] dann jaejun yoo
byJaeJun Yoo
 
PDF
Introduction to ambient GAN
byJaeJun Yoo
 
PDF
[PR12] understanding deep learning requires rethinking generalization
byJaeJun Yoo
 
PDF
Rethinking Data Augmentation for Image Super-resolution: A Comprehensive Anal...
byJaeJun Yoo
 
PDF
[PR12] Spectral Normalization for Generative Adversarial Networks
byJaeJun Yoo
 
PDF
[CVPR2020] Simple but effective image enhancement techniques
byJaeJun Yoo
 
PDF
[PR12] Generative Models as Distributions of Functions
byJaeJun Yoo
 
PDF
[PR12] intro. to gans jaejun yoo
byJaeJun Yoo
 
[PR12] categorical reparameterization with gumbel softmax
byJaeJun Yoo
 
A beginner's guide to Style Transfer and recent trends
byJaeJun Yoo
 
[PR12] Inception and Xception - Jaejun Yoo
byJaeJun Yoo
 
Variants of GANs - Jaejun Yoo
byJaeJun Yoo
 
[PR12] PixelRNN- Jaejun Yoo
byJaeJun Yoo
 
[PR12] Capsule Networks - Jaejun Yoo
byJaeJun Yoo
 
[Pr12] dann jaejun yoo
byJaeJun Yoo
 
Introduction to ambient GAN
byJaeJun Yoo
 
[PR12] understanding deep learning requires rethinking generalization
byJaeJun Yoo
 
Rethinking Data Augmentation for Image Super-resolution: A Comprehensive Anal...
byJaeJun Yoo
 
[PR12] Spectral Normalization for Generative Adversarial Networks
byJaeJun Yoo
 
[CVPR2020] Simple but effective image enhancement techniques
byJaeJun Yoo
 
[PR12] Generative Models as Distributions of Functions
byJaeJun Yoo
 
[PR12] intro. to gans jaejun yoo
byJaeJun Yoo
 

Recently uploaded

PDF
Kubernetes Cloud Native Indonesia Meetup - January 2026
byPrasta Maha
 
PPTX
Mastering SQL Server Replication: Types, Setup & Troubleshooting
byGeoPITS Global Pvt Ltd
 
PPTX
Apache Kafka 101 for Techies in IT dep.pptx
byamulyareddyk97
 
PPTX
SOFTWARE DEVELOPMENT PROCESS - INTRODUCTION
byParithi Thamizh
 
PDF
How to Design Premium Health (Public Health) PPT Using AI? Top Strategies
byPublic Health Concern Nepal
 
PDF
Getting the Best of TrueDEM – January News & Updates
bypanagenda
 
PDF
Introduction to Linux and Basic Commands
byiDev Semarang
 
PDF
Transcript: What ONIX can do: Leveraging metadata to support the discoverabil...
byBookNet Canada
 
PDF
Agentic AI Roadmap 2026: Mastering Autonomous AI Workflows and Systems
byAeafat Ahmed Mubin
 
PDF
Azure DevOps Managed Services: Driving Speed, Security, and Business Growth
byjohncarterjn
 
PPTX
Understanding-Search-Algorithms_09-12-25.pptx
byshaikmahammedtauheed
 
PPTX
AI Meets DBA Transforming Database Administration with Intelligence
byGeoPITS Global Pvt Ltd
 
PDF
Ethical AI applied to publishing: Presenting wâsikan kisewâtisiwin, an AI too...
byBookNet Canada
 
PDF
Router-DHCP-Printer-SharingRouter-DHCP-Printer-Sharing
byarbendi2160
 
PDF
Teaching Robots how to Read 1/2: AI Center & Classic Document Understanding (...
byanabulhac
 
PPTX
API Gateway Architecture - Technical Report 2026
byPowersoft2026
 
PPTX
AI in Marine Insurance Future of Smarter Risk, Faster Claims & Safer Shipping...
byAutomationEdge Technologies
 
PPTX
CRM for the Insurance Industry Lessons for Insurance CIOs and Digital Leaders...
byKerry Millar
 
PPTX
Dell poweredge-customer-presentation.pptx
byhungungphu123
 
PPTX
AI and Digital Transformation Solutions.
byBuildingblocks
 
Kubernetes Cloud Native Indonesia Meetup - January 2026
byPrasta Maha
 
Mastering SQL Server Replication: Types, Setup & Troubleshooting
byGeoPITS Global Pvt Ltd
 
Apache Kafka 101 for Techies in IT dep.pptx
byamulyareddyk97
 
SOFTWARE DEVELOPMENT PROCESS - INTRODUCTION
byParithi Thamizh
 
How to Design Premium Health (Public Health) PPT Using AI? Top Strategies
byPublic Health Concern Nepal
 
Getting the Best of TrueDEM – January News & Updates
bypanagenda
 
Introduction to Linux and Basic Commands
byiDev Semarang
 
Transcript: What ONIX can do: Leveraging metadata to support the discoverabil...
byBookNet Canada
 
Agentic AI Roadmap 2026: Mastering Autonomous AI Workflows and Systems
byAeafat Ahmed Mubin
 
Azure DevOps Managed Services: Driving Speed, Security, and Business Growth
byjohncarterjn
 
Understanding-Search-Algorithms_09-12-25.pptx
byshaikmahammedtauheed
 
AI Meets DBA Transforming Database Administration with Intelligence
byGeoPITS Global Pvt Ltd
 
Ethical AI applied to publishing: Presenting wâsikan kisewâtisiwin, an AI too...
byBookNet Canada
 
Router-DHCP-Printer-SharingRouter-DHCP-Printer-Sharing
byarbendi2160
 
Teaching Robots how to Read 1/2: AI Center & Classic Document Understanding (...
byanabulhac
 
API Gateway Architecture - Technical Report 2026
byPowersoft2026
 
AI in Marine Insurance Future of Smarter Risk, Faster Claims & Safer Shipping...
byAutomationEdge Technologies
 
CRM for the Insurance Industry Lessons for Insurance CIOs and Digital Leaders...
byKerry Millar
 
Dell poweredge-customer-presentation.pptx
byhungungphu123
 
AI and Digital Transformation Solutions.
byBuildingblocks
 

Super resolution in deep learning era - Jaejun Yoo

  • 1.
    Super-resolution in deep learningera Jaejun Yoo Ph.D. AI Scientist @NAVER Clova AI Seminar, Math Dept., KAIST
  • 2.
    System (H) noise Inverse problem unknown original data model𝒚 = 𝑯(𝒙) + 𝒏 observed data ? ? ? Inverse problems
  • 3.
    Inverse problems: scattering Maxwellequation Láme equation noise Inverse problem Restored density original density model 𝒚 = 𝑯(𝒙) + 𝒏 * Yoo J et al., SIAM, 2016 observed field e.g. electromagnetic, or acoustic wave physical property reconstruction* or source localization
  • 4.
    Blurring, Down Sampling noise Inverse problem Restored image originalimage model 𝒅 = 𝑮(𝒙) + 𝒏 * Bae W and Yoo J, CVPRW, 2017 observed image e.g. natural images denoising & super-resolution* Inverse problems: image restoration (IR)
  • 5.
    System (H) noise model 𝒚= 𝑯(𝒙) + 𝒏 Image restoration (IR) By specifying different degradation operator H, one can correspondingly get different IR tasks. Deblurring or Deconvolution : 𝑯𝒙 = 𝒌 ⊛ 𝒙 Super-resolution : 𝑯𝒙 = (𝒌 ⊛ 𝒙) ↓ 𝒔 Denoising : 𝑯𝒙 = 𝑰𝒙 Inpainting : 𝑯𝒙 = 𝑰 𝒎𝒊𝒔𝒔𝒊𝒏𝒈 𝒙 General formulation of IR problems:
  • 6.
    Given a singleimage 𝒚, solve f𝐨𝐫 𝒙: • 𝒚: known low resolution (LR) image • 𝒙: unknown high resolution (HR) image • 𝒌: unknown blur kernel (typically set as identity) • ↓ 𝒔: downsample 𝒙 by the factor of 𝒔 (typically done by bicubic function) • 𝒏: additive white Gaussian noise (AWGN) Single Image Super-Resolution 𝒚 = 𝒌 ⊛ 𝒙 ↓ 𝒔 + 𝒏
  • 7.
    Image restoration (IR) 𝑯𝒙= 𝟏, 𝟎, 𝟏, 𝟎 𝟎, 𝟏, 𝟎, 𝟏 𝟏, 𝟏, 𝟎, 𝟎 𝟎, 𝟎, 𝟏 𝟏 𝑨 𝑩 𝑪 𝑫 , 𝒓𝒂𝒏𝒌 𝑯 = 𝟒 A B DC 1 0 00 01 1 0 body 𝒘𝒆𝒍𝒍 − 𝒑𝒐𝒔𝒆𝒅 𝒑𝒓𝒐𝒃𝒍𝒆𝒎, ∃𝑯−𝟏 more constraints, assumptions, regularization, iterative methods, etc. How we solve the problem? • To find the best model 𝑯 such that 𝒚 = 𝑯 𝒙 + 𝒏 • In linear system, e.g. X-ray CT, we minimize the following cost function: • In signal processing society: 𝐲 = 𝐇𝐱, 𝝓 = 𝒚 − 𝑯𝒙 𝟐 𝟐
  • 8.
    Image restoration (IR) FromBayesian perspective, the solution ෝ𝒙 can be obtained by solving a Maximum A Posteriori (MAP) problem: ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐚𝐱 𝒙 𝒍𝒐𝒈 𝒑 𝒚 𝒙 + 𝒍𝒐𝒈 𝒑(𝒙) ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) More formally, data fidelity regularization Enforces desired property of the output Guarantees the solution accords with the degradation process 1) Model-based optimization 2) Discriminative learning methods : What kinds of prior knowledge can we “impose on” our model?
  • 9.
    Model-based optimization methods Whatkinds of prior knowledge can we “impose on” our model? • Sparsity • Wavelets, DCT, PCA, etc. • Dictionary learning • e.g., K-SVD • Nonlocal self-similarity • BM3D • Low-rankness ෝ𝜶 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝜶 𝟏 𝟐 𝒚 − 𝑯𝑫𝜶 𝟐 + 𝝀 𝜶 𝟏 ෡𝑿 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝑿 𝟏 𝟐 𝒀 − 𝑿 𝟐 + 𝝀 𝑿 ∗
  • 10.
    Image restoration (IR) FromBayesian perspective, the solution ෝ𝒙 can be obtained by solving a Maximum A Posteriori (MAP) problem: ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐚𝐱 𝒙 𝒍𝒐𝒈 𝒑 𝒚 𝒙 + 𝒍𝒐𝒈 𝒑(𝒙) ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) More formally, data fidelity regularization Enforces desired property of the output Guarantees the solution accords with the degradation process 1) Model-based optimization 2) Discriminative learning methods What kinds of prior knowledge can we “learn using” our model? :
  • 11.
    Discriminative learning methods Whatkinds of prior knowledge can we “learn using” our model? 𝐦𝐢𝐧 𝜽 𝒍 ෝ𝒙, 𝒙 , 𝒔. 𝒕. ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙; 𝜽) ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) data fidelity regularization Here, we learn the prior parameter 𝜽: through an optimization of a loss function 𝒍 on a training set (image pairs).
  • 12.
    Discriminative learning methods CNNs(𝒇) 𝒚 𝒙 Conv, ReLU, pooling, etc. General statement of the problem: 𝐦𝐢𝐧 𝜽 𝒍 ෝ𝒙, 𝒙 , 𝒔. 𝒕. ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙; 𝜽) By replacing MAP inference with a predefined nonlinear function ෝ𝒙 = 𝒇 𝒚, 𝑯, 𝜽 , solving IR problem with CNNs can be treated as one of the discriminative learning methods. learn the image prior model
  • 13.
    SRCNN The start ofdeep learning in SISR • Link the CNN architecture to the traditional “sparse coding” methods. • The first end-to-end framework: each module is optimized through the learning process
  • 14.
    SRCNN Set5 dataset withan upscaling factor × 𝟑 SNCNN Surpasses the bicubic baseline and outperforms the sparse coding based method. The first-layer filters trained on upscaling factor × 𝟑 Example feature maps of different layers. Results
  • 15.
    SRCNN Problems left • BicubicLR input usage: pros & cons • Shallow (three-layer) network design • Naive & implicit prior
  • 16.
    • Upsampling methods •Interpolation-based vs. Learning-based • Model framework • Pre-, Post-, Progressive- upsampling • Iterative up-and-down sampling • Network design • Residual learning • Recursive learning • Deeper & Denser • Etc. Developments of deep models in SISR
  • 17.
    Pre- vs. Post-upsampling Progressive-upsampling Model framework LapSRN: motivated from Laplacian Image Pyramid • LapSRN (CVPR ‘17) • ProSR (CVPR ‘18) • Early stage • SRCNN (ECCV ‘14) • FSRCNN (ECCV ‘16)
  • 18.
    Pre- vs. Post-upsampling Progressive-upsampling Iterative up-and-down sampling Model framework BPDN: motivated from iterative projection in the optimization methods. Super-resolution result on 8× enlargement. PSNR: LapSRN (15.25 dB), EDSR (15.33 dB), and BPDN (16.63 dB) • Deep Back-Projection Network (CVPR ‘18) • LapSRN (CVPR ‘17) • ProSR (CVPR ‘18) • Early stage • SRCNN (ECCV ‘14) • FSRCNN (ECCV ‘16)
  • 19.
    Variety of modeldesigns • Residual learning • Recursive learning • Deeper & Denser • Exploit Non-local or Attention • GANs • Etc. Network design
  • 20.
    Variety of modeldesigns Network design
  • 21.
    VDSR (CVPR ‘16) Networkdesign: 1st cornerstone, residual learning Very Deep SR network • The first “deep” network (20 layers) • Proposed a practical method to actually train the “deep” layers (before BN)
  • 22.
    VDSR (CVPR ‘16) Networkdesign: 1st cornerstone, residual learning Very Deep SR network • The first “deep” network (20 layers) • Proposed a practical method to actually train the “deep” layers
  • 23.
    Network design: recursivelearning DRCN (CVPR ‘16), DRRN (CVPR ‘17), MemNet (ICCV ‘17) • Reuse the module (less parameters, smaller network)
  • 24.
    Network design: recursivelearning DRCN (CVPR ‘16), DRRN (CVPR ‘17), MemNet (ICCV ‘17) • Reuse the module (less parameters, smaller network)
  • 25.
    Network design: deeper& denser SRResNet (CVPR ‘17), SRDenseNet (ICCV ‘17) • Deeper (ResNet backbone) • Denser (DenseNet backbone)
  • 26.
    Network design: deeper& denser SRResNet (CVPR ‘17), SRDenseNet (ICCV ‘17) • Deeper (ResNet backbone) • Denser (DenseNet backbone)
  • 27.
    Network design: 2ndcornerstone EDSR (CVPR ‘17) • The first to provide a backbone for “SR” task • Remove batch normalization • Residual scaling • Very stable and reproducible model • Removed batch normalization layers • Self-geometric ensemble method • Exploit pretrained 2x model for the other scales • Performance gain • Model size reduction (43M → 8M) • Flexibility (partially scale agnostic)
  • 28.
    Network design: 2ndcornerstone EDSR (CVPR ‘17)
  • 29.
    Network design: 2ndcornerstone EDSR (CVPR ‘17)
  • 30.
    Network design Non-local &Attention module Generative Adversarial Networks in Super-resolution • "Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network" (SRGAN, CVPR ‘17) • "A fully progressive approach to single-image super-resolution" (ProSR, CVPR ‘18) • "ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks" ECCV ‘18 • Candidate of 4th cornerstone? • "2018 PIRM Challenge on Perceptual Image Super-resolution" (ECCV ‘18) • 3rd cornerstone; at least in the perspective of the performance; too sensitive, many hyper-params. • "Image Super-Resolution Using Very Deep Residual Channel Attention Networks" (RCAN, ECCV ‘18) • "Non-local Recurrent Network for Image Restoration" (NLRN, NIPS ‘18) • "Residual Non-local Attention Networks for Image Restoration" (RNAN, ICLR ‘19)
  • 31.
    GANs in SR:candidate of 4th cornerstone? Problems • Cannot go along with traditional metrics: PSNR / SSIM • New metric?; "2018 PIRM Challenge on Perceptual Image Super-resolution" (ECCV ‘18) ProSRGAN (CVPR ‘18)
  • 32.
    Summary (until now) Methods Generalformulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) • Hand-crafted priors • Sparsity • Low-rankness • Learned discriminative priors • Predefined nonlinear function • CNNs 1) Model-based optimization 2) Discriminative learning methods
  • 33.
    Pros General to handledifferent IR problems Clear physical meanings Data-driven end-to-end learning Efficient inference during test-phase Cons Hand-crafted priors (weak representations) Optimization task is time-consuming Generality of model is limited Interpretability of model is limited Summary (until now) Methods 1) Model-based optimization 2) Discriminative learning methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙)
  • 34.
    Pros General to handledifferent IR problems Clear physical meanings Data-driven end-to-end learning Efficient inference during test-phase Cons Hand-crafted priors (weak representations) Optimization task is time-consuming Generality of model is limited Interpretability of model is limited Summary (until now) Methods 1) Model-based optimization 2) Discriminative learning methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) “Can we somehow get the best of both worlds?”
  • 35.
    Getting the bestof both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛
  • 36.
    Getting the bestof both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌)
  • 37.
    Getting the bestof both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 In Bayesian perspective, this is Gaussian denoising subproblem with noise level 𝝀/𝝁!𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌)
  • 38.
    Getting the bestof both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁)𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌)
  • 39.
    Getting the bestof both worlds Variable Splitting Methods • Want to separately deal with the data fidelity term and the regularization terms • Specifically, the regularization term only corresponds to a denoising subproblem • Alternating Direction Method of Multipliers (ADMM), Half Quadratic Splitting (HQS) • Cost function of HQS: ℒ 𝝁 𝒙, 𝒛 = 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 + 𝝁 𝒛 − 𝒙 𝟐 ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽 𝒛 𝒔. 𝒕. 𝒛 = 𝒙 𝒙 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝁 𝒙 − 𝒛 𝒌 𝟐 , 𝒛 𝒌+𝟏 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒛 𝟏 𝟐 𝝀/𝝁 𝟐 𝒛 − 𝒙 𝒌+𝟏 𝟐 + 𝚽 𝒛 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁)𝒙 𝒌+𝟏 = 𝑯 𝑻 𝑯 + 𝝁𝑰 −𝟏 (𝑯𝒚 + 𝝁𝒛 𝒌) 1. Any gray or color denoisers to solve a variety of inverse problems. 2. The explicit image prior can be unknown in solving the original equation. 3. Several complementary denoisers which exploit different image priors can be jointly utilized to solve one specific problem.
  • 40.
    IRCNN HQS: Plug andPlay • Image Restoration with CNN Denoiser Prior • Kai Zhang et al. “Learning Deep CNN Denoiser Prior for Image Restoration” 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁)
  • 41.
    IRCNN HQS: Plug andPlay • Image Restoration with CNN Denoiser Prior • Kai Zhang et al. “Learning Deep CNN Denoiser Prior for Image Restoration” 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁) Image deblurring performance comparison for Leaves image (the blur kernel is Gaussian kernel with standard deviation 1.6, the noise level σ is 2).
  • 42.
    IRCNN HQS: Plug andPlay • Image Restoration with CNN Denoiser Prior • Kai Zhang et al. “Learning Deep CNN Denoiser Prior for Image Restoration” 𝒛 𝒌+𝟏 = 𝑫𝒆𝒏𝒐𝒊𝒔𝒆𝒓 (𝒙 𝒌+𝟏, 𝝀/𝝁) SISR performance comparison for Set5: IRCNN can tune the blur kernel and scale factor w/o training. (the blur kernel is 7×7 Gaussian kernel with standard deviation 1.6, the scale factor × 3)
  • 43.
    Pros General to handledifferent IR problems Clear physical meanings Data-driven end-to-end learning Efficient inference during test-phase Cons Hand-crafted priors (weak representations) Optimization task is time-consuming Generality of model is limited Interpretability of model is limited Summary (until now) Methods 1) Model-based optimization 2) Discriminative learning methods General formulation of IR ෝ𝒙 = 𝒂𝒓𝒈𝐦𝐢𝐧 𝒙 𝟏 𝟐 𝒚 − 𝑯𝒙 𝟐 + 𝝀𝚽(𝒙) √√
  • 44.
    DPSR (CVPR ‘19) DeepPlug and Play Super-Resolution for Arbitrary Blur Kernels
  • 45.
    Problems yet tobe solved • It WORKS but NO WHYS. • Many studies are just blindly suggesting a new architecture that works. • Recent architecture are (kind of) overfitted to the dataset. • Bicubic downsampling tasks are saturated. (fails in other d/s scheme or realistic noises) • We need more “realistic” and “pragmatic” model that works in real environments. • Lack of fair comparisons • Lighter (greener) and faster (inference) models • New architectures (more than just a shared parameters) • New methods
  • 46.
    Jaejun Yoo Ph.D. ResearchScientist @NAVER Clova AI Research, South Korea Interested in Generative models, Signal Processing, Interpretable AI, and Algebraic Topology Techblog: https://jaejunyoo.blogspot.com Github: https://github.com/jaejun-yoo / LinkedIn: www.linkedin.com/in/jaejunyoo Research Keywords deep learning, inverse problem, signal processing, generative models Thank you Q&A?