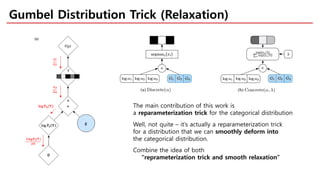
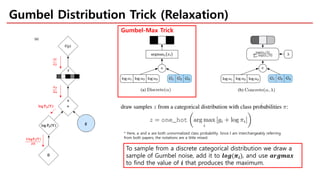
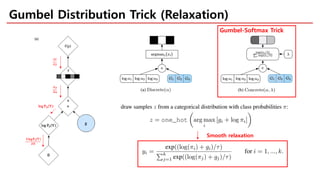
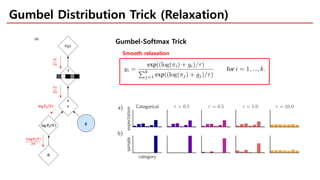
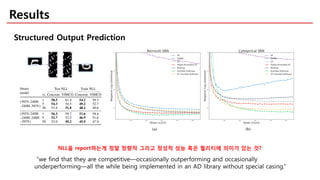
The document discusses categorical reparameterization using the Gumbel-Softmax method, highlighting its advantages for dealing with discrete random variables in stochastic computation graphs. It explains the challenges of optimizing these graphs, particularly during the backward pass, and introduces a novel reparameterization trick that allows for smooth relaxation to a categorical distribution. Additionally, the effectiveness and implementation simplicity of the Gumbel-Softmax trick are emphasized, alongside references for further exploration.

1. Categorical Reparameterization with
Gumbel-Softmax
PR12와 함께 이해하는
Jaejun Yoo
Clova ML / NAVER
PR12
4th Mar, 2018

2. The Concrete Distribution: A Continuous Relaxation of
Discrete Random Variables
by C.J. Mddison, A. Mnih, Y. W. Teh
Nov. 2016: https://arxiv.org/abs/1611.00712
Today’s contents
NIPS 2016 workshop / ICLR 2017
Categorical Reparameterization with Gumbel-Softmax
by E. Jang, S. Gu, B. Poole
Nov. 2016: https://arxiv.org/abs/1611.01144

3. 들어가기 전에 잠시 한탄…
“Trust me. It’s complicated….”
금새 볼 줄 알고 덤볐다가 매우 시간 잡
아먹은 논문입니다. 내 주말..Orz…

4. Motivation
How do we deal with stochastic nodes with discrete
random variables?

5. Optimizing Stochastic Computation Graphs
Forward pass of SCG

6. Optimizing Stochastic Computation Graphs
Backward pass of SCG
Challenging part

7. Optimizing Stochastic Computation Graphs
Backward pass of SCG
Challenging part
1) Score Function Estimators
2) Reparameterization Trick

8. Score Function Estimators
Challenging part

9. Score Function Estimators
Challenging part
“Still, there remains an issue of high variance.”

10. Score Function Estimators
Challenging part
“Still, there remains an issue of high variance.”
• This is NOT universally true. There is no proof
• Good discussion in Section 3.1 in Yarin Gal’s Thesis

11. Reparameterization Trick

12. Why things go wrong in DISCRETE cases?
“Is this defined?”
“we cannot backpropagate the gradients through
discrete nodes in the computational graph”.
Discrete node

13. Gumbel Distribution Trick (Relaxation)
The main contribution of this work is
a reparameterization trick for the categorical distribution
Well, not quite – it’s actually a reparameterization trick
for a distribution that we can smoothly deform into
the categorical distribution.
Combine the idea of both
“reprameterization trick and smooth relaxation”

14. Gumbel Distribution Trick (Relaxation)
Gumbel-Max Trick
* Here, 𝛼𝛼 and 𝜋𝜋 are both unnormalized class probability. Since I am interchangeably referring
from both papers, the notations are a little mixed.
To sample from a discrete categorical distribution we draw a
sample of Gumbel noise, add it to 𝒍𝒍𝒍𝒍 𝒍𝒍(𝝅𝝅𝒊𝒊), and use 𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂𝒂
to find the value of 𝒊𝒊 that produces the maximum.

15. Gumbel Distribution Trick (Relaxation)
Gumbel-Softmax Trick
Smooth relaxation

16. Gumbel Distribution Trick (Relaxation)
Smooth relaxation
Gumbel-Softmax Trick

17. Advantage of Gumbel Trick
• Biased but low variance estimator
(Biased estimator w.r.t. original discrete objective but low variance & unbiased
estimator w.r.t. continuous surrogate objective)
• Plug & play (easy to code and implement)
• Computational efficiency
• Better performance

18. Implementation (Super easy)
def gumbel_max_sample(x):
z = gumbel(loc=0, scale=1, size=x.shape)
return (x + g).argmax(axis=1)
Inverse Transform Sampling
Smoothing relaxation
𝑭𝑭 𝒙𝒙 = 𝐞𝐞𝐞𝐞 𝐩𝐩 − 𝐞𝐞𝐞𝐞𝐞𝐞 −𝒙𝒙 ⟹ 𝐗𝐗 = −𝐥𝐥𝐥𝐥𝐥𝐥(−𝐥𝐥𝐥𝐥𝐥𝐥 𝐔𝐔 )

19. Results
Structured Output Prediction
NLL을 report하는게 정말 정량적 그리고 정성적 성능 혹은 퀄리티에 의미가 있는 것?
“we find that they are competitive—occasionally outperforming and occasionally
underperforming—all the while being implemented in an AD library without special casing.”

20. References
• https://www.youtube.com/watch?v=JFgXEbgcT7g (presentation, YouTube)
• https://github.com/ericjang/gumbel-softmax/blob/master/Categorical%20VAE.ipynb
(code)
• https://blog.evjang.com/2016/11/tutorial-categorical-variational.html (blog)
• https://casmls.github.io/general/2017/02/01/GumbelSoftmax.html (blog)

22. Inverse Transform Sampling
균등 분포의 보편성과 난수 생성기 만들기
𝑼𝑼 ~ 𝑼𝑼𝑼𝑼𝑼𝑼𝑼𝑼 𝟎𝟎, 𝟏𝟏 , 𝑿𝑿 = 𝑭𝑭−𝟏𝟏(𝑼𝑼)
임의의 확률 분포를 따르는 확률 변수 𝑿𝑿에 난수를 추출하고 싶다면?
확률 변수 X의 누적 분포 함수(CDF) 𝑭𝑭(𝒙𝒙)의 역함수 𝑭𝑭−𝟏𝟏
를 알 수 있다면
기본 난수 생성기를 이용하여 확률 변수 𝑿𝑿에 대한 난수 생성기를 만들 수 있다.
즉, 균등 분포만 있으면 다른 모든 분포를 만들어낼 수 있다.
e.g. Standard Gumbel:
http://www.boxnwhis.kr/2017/04/13/how_to_make_random_number_generator_for_any_probability_distribution.html
𝑭𝑭 𝒙𝒙 = 𝐞𝐞𝐞𝐞 𝐩𝐩 − 𝐞𝐞𝐞𝐞𝐞𝐞 −𝒙𝒙 ⟹ 𝐗𝐗 = −𝐥𝐥𝐥𝐥𝐥𝐥(−𝐥𝐥𝐥𝐥𝐥𝐥 𝐔𝐔 )