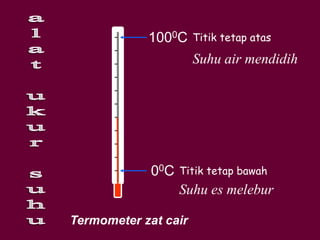
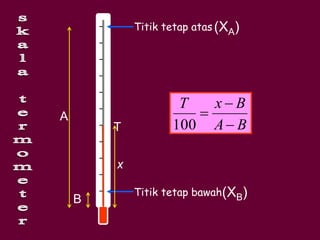
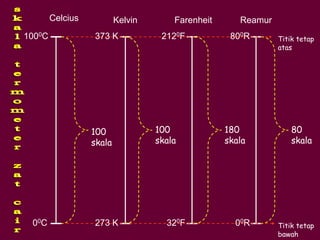
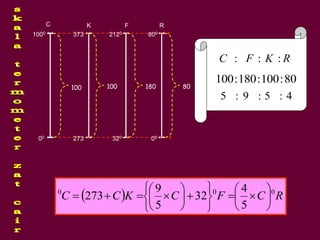
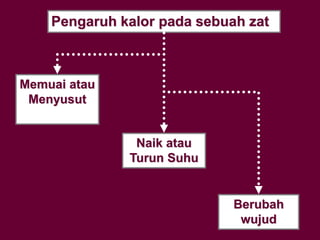
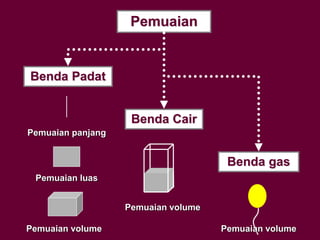
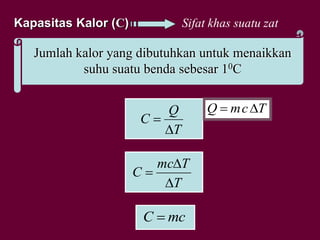
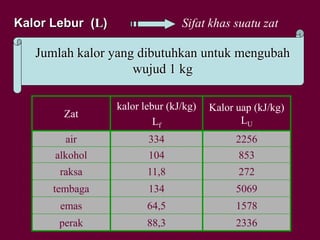
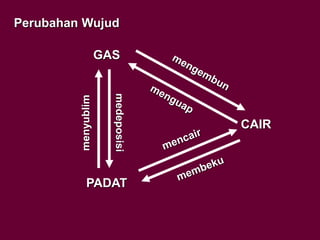
Dokumen tersebut membahas tentang definisi suhu dan kalor serta hubungannya dengan pemuaian dan kenaikan suhu benda. Secara khusus dijelaskan tentang koefisien pemuaian berbagai zat dan contoh perhitungan soal terkait kenaikan suhu dan volume benda akibat perpindahan kalor.

1. Created by Mrs Mary

2. Suhu adalah derajat panas atau dingin suatu benda
Defenisi Suhu
kalor merupakan salah satu bentuk perpindahan
energi dari benda bersuhu tinggi ke benda
bersuhu lebih rendah
Defenisi Kalor

3. Termometer zat cair
00C
1000C
Titik tetap bawah
Titik tetap atas
Suhu es melebur
Suhu air mendidih

4. (XB)
(XA)
Titik tetap bawah
Titik tetap atas
B
A
T
x
BA
BxT



100

5. Contoh 1
Sebuah termometer ketika diletakkan dalam es
yang meleleh, ketinggian raksanya 20 mm. Lalu
ketika diletakkan dalam air yang mendidih,
ketinggian raksanya 100 mm. Ketika termometer
itu diletakkan dalam cairan tertentu, ketinggian
air raksa adalah 45 mm. Berapa suhu cairan itu?
Penyelesaian
B = 20 mm
A = 100 mm
x = 45 mm
T ?
BA
BxT



100

6. Contoh 1
20100
2045
100 


T
80
25
100

T
1002580 T
250080 T
80
2500
T
0
25,31
Suhu cairan 31,250
BA
BxT



100

7. Kelvin
00C
1000C
273 K
373 K
320F
2120F
00R
800R
Celcius Farenheit Reamur
Titik tetap
bawah
Titik tetap
atas
100
skala
100
skala
180
skala
80
skala

8. K
00
1000
273
373
320
2120
00
800
C F R
100 100 180 80
RKFC :::
4:5:9:5
  RCFCKCC 000
5
4
32
5
9
273 



















80:100:180:100

9. Contoh 2
FCC












 000
32
5
9
FC












 000
3237
5
9
37
 FC 00
326.6637 
Suhu badan manusia rata-rata 370 C, nyatakan
dalam skala Fahrenheit
Penyelesaian
C = 370C
F?
FC 00
6.9837 

10. Pengaruh kalor pada sebuah zat
Memuai atau
Menyusut
Naik atau
Turun Suhu
Berubah
wujud

11. Pemuaian
Benda Padat
Benda Cair
Benda gas
Pemuaian volume
Pemuaian luas
Pemuaian panjang
Pemuaian volume
Pemuaian volume

12. Pemuaian Panjang
Terjadi pada benda padat satu dimensi (hanya memiliki
panjang)
l0
Sebelum dipanaskan, suhu T0Sesudah dipanaskan, suhu T
l
l0 = panjang awal benda (m)
l = panjang akhir benda (m)
Δl
Δl = pertambahan panjang (m)
T0 = suhu awal benda (0C atau K)
T = suhu akhir benda (0C atau K)
Δl = l – l0
ΔT = kenaikan suhu (0C atau K)
ΔT = T – T0

13. Pemuaian Panjang
Tll  0
Δl = pertambahan panjang (m) = l – l0
α = koefisien muai panjang ( /0C )
l0 = panjang awal benda (m)
ΔT = kenaikan suhu (0C atau K)
= T – T0

14. Koefisien muai panjang (α )berbagai zat
pada suhu kamar
Zat α (0C) -1
Kaca 9 x 10-6
Baja 11 x 10-6
Tembaga 17 x 10-6
alumunium 24 x 10-6
Timah hitam 29 x 10-6
invar 0,9 x 10-6
1 m kaca bila dipanaskan 10C akan bertambah panjang 9 x 10-6 m1 cm kaca bila dipanaskan 10C akan bertambah panjang 9 x 10-6 cm1 m baja bila dipanaskan 10C akan bertambah panjang 11 x 10-6 m

15. Contoh 3
Sebuah jembatan yang terbuat dari baja memiliki
panjang 500 m. Suhu minimum yang dicapai
pada musim hujan adalah 100C dan suhu
maksimum yang dicapai pada musim kemarau
adalah 400C. Tentukan lebar celah yang harus
disediakan pada salah satu ujung jembatan untuk
memperhitungkan efek pemuaian!(koefisien muai
baja 11 x 10-6 /0C)
Diketahui
l0 = 500 m
T0 = 100C
T = 400C
α = 11 x 10-6 /0C
Ditanya
Δl?
Tll  0

16. Penyelesaian
Tll  0
)( 00 TTll  
)1040(5001011 6
 
l
30105500 6
 
l
ml 165,0
Panjang celah pada salah satu ujung
jembatan adalah 0,165 m
Contoh 3

17. Pemuaian Luas
Terjadi pada benda padat dua dimensi (memiliki
panjang dan lebar)
Sebelum dipanaskan, suhu T0Sesudah dipanaskan, suhu T
A0 = luas awal benda (m2)
A = luas akhir benda (m2)
ΔA = pertambahan luas (m2)
T0 = suhu awal benda (0C atau K)
T = suhu akhir benda (0C atau K)
ΔA = A – A0
ΔT = kenaikan suhu (0C atau K)
ΔT= T – T0
A0A

18. Pemuaian Luas
TAA  0
ΔA= pertambahan luas (m2) = A – A0
β = koefisien muai luas ( /0C )
A0 = luas awal benda (m2)
ΔT = kenaikan suhu (0C atau K)= T – T0
= 2α

19. Contoh 4
2
0 4 rA 
Sebuah bola berongga terbuat dari perunggu
(koefisien muai linier α = 18 x 10-6 ?0C) pada suhu
00C. Jari-jarinya 1 m. Jika bola tersebut
dipanaskan sampai 800C, berapa pertambahan
luas permukaan bola?
α = 11 x 10-6 /0C
Diketahui
T0 = 00C
T = 800C
r0 = 1 m
Ditanya ΔA?
2
0 14  A
40 A
Penyelesaian
TAA  0

20. Penyelesaian
TAA  0
  )(2 00 TTAA  
  )080(410182 6
 
A
8041036 6
 
A
2
1152,0 mA 
Pertambahan luas permukaan bola
adalah 0,1152π m2
Contoh 4

21. Pemuaian Volume
Terjadi pada benda padat tiga dimensi (memiliki
panjang dan lebar dan tinggi)
Sebelum dipanaskan, suhu T0Sesudah dipanaskan, suhu T
V0 = volume awal benda (m3)
V = volume akhir benda (m3)
ΔV = pertambahan volume (m3)
T0 = suhu awal benda (0C atau K)
T = suhu akhir benda (0C atau K)
ΔV = V – V0
ΔT = kenaikan suhu (0C atau K)
ΔT= T – T0
V0V

22. Pemuaian Volume
TVV  0
ΔV = pertambahan luas (m3)= V – V0
γ = koefisien muai volume ( /0C )
V0 = volume awal benda (m3)
ΔT = kenaikan suhu (0C atau K) = T – T0
= 3α

23. Koefisien muai volume (γ) berbagai zat cair
pada suhu kamar
Zat γ (0C) -1
air 2,1 x 10-4
alkohol 1,12 x 10-3
raksa 1,82 x 10-3
bensin 9,6 x 10-3
udara 3,67 x 10-3
helium 3,665 x 10-3
1 L air bila dipanaskan 10C akan bertambah volumenya 2,1 x 10-4 L1 cm3 air bila dipanaskan 10C akan bertambah volumenya 2,1 x 10-4 cm31 L bensin bila dipanaskan 10C akan bertambah volumenya 9,6 x 10-3 L

24. Contoh 5
Sebuah tangki bensin pada mobil memiliki
kapasitas 40 L pada suhu 200C. Jika tangki diisi
bensin sampai penuh, berapa banyak bensin
akan meluber jika mobil dipanaskan di bawah
sinar terik matahari sehingga suhu tangki
mencapai 450C. (Abaikan pemuaian kecil dari
tangki itu sendiri!)
Diketahui
T0 = 200C
T = 450C
V0 = 40 L
Ditanya
γ bensin = 9,6 x 10-3 /0C
ΔV?
TVV  0

25. Penyelesaian
TVV  0
)( 00 TTVV  
  )2045(40106,9 3
 
V
2540106,9 3
 
V
LV 6,9
Bensin yang meluber adalah 9,6 L
Contoh 5

26. Contoh 6
Sebuah bejana kaca pada 00X terisi penuh
dengan 100 cm3 raksa. Jika suhu dinaikkan
menjadi 200C, berapa cm3 raksa yang akan
tumpah?
Diketahui
T0 = 00C
T = 200C
V0 kaca = V0 kaca = 100 cm3
Ditanya
α kaca = 9 x 10-6 /0C volum raksa yang
tumpah (ΔV)?
γ raksa = 1,82 x 10-3 /0C
ΔV = ΔVraksa - ΔVkaca
TVV  0

27. Penyelesaian
TVV  0
)(3 00 TTVV kacakacakaca  
  )020(1001093 6
 
kacaV
33
054,01054 cmVkaca  
)( 00 TTVV raksaraksaraksa  
  )020(1001082,1 3
 
raksaV
3
64,3 cmVraksa 
333
586,3054,064,3 cmcmcmVVV kacaraksa 
Contoh 6

28. HUBUNGAN KALOR DAN KENAIKAN SUHU
m1
m2
Bagaimana hubungan banyaknya kalor (Q) yang diperlukan
untuk menaikan suhu dengan massa benda (m)?
Semakin besar massa (m) benda semakin banyak kalor
(Q) yang dibutuhkan untuk menaikkan suhunya
Q ~ m

29. HUBUNGAN KALOR DAN KENAIKAN SUHU
Apakah jumlah kalor (Q) yang diperlukan untuk menaikkan
suhu bergantung pada jenis zat (c)?
Jumlah kalor (Q) yang diperlukan untuk menaikan suhu
berbeda untuk setiap jenis zat
Q ~ c
airminyak

30. HUBUNGAN KALOR DAN KENAIKAN SUHU
Bagaimana hubungan kenaikan suhu (ΔT) dengan jumlah
kalor yang diperlukan?
Semakin besar kenaikkan suhunya semakin besar
jumlah kalor yang diperlukan
Q ~ ΔT
ΔT = 800CΔT = 400C

31. HUBUNGAN KALOR DAN KENAIKAN SUHU
TcmQ 
Q = Jumlah kalor yang diperlukan untuk menaikkan
suhu suatu zat ( joule)
m = Massa zat (kg)
c = Kalor jenis zat (joule/kg0C)
ΔT = Kenaikan suhu zat (0C) = T – T0
Suhu akhir zat (0C)
Suhu awal zat (0C)
Q ~ m Q ~ c Q ~ ΔT

32. Kalor Jenis Zat (c)
Jumlah kalor yang dibutuhkan untuk menaikkan
suhu 1 kg zat sebesar 10C
Zat c (J/kg0C)
air 4200
alumunium 900
raksa 140
tembaga 390
besi atau baja 450
alkohol 2400
Sifat khas suatu zat

33. Kapasitas Kalor (C)
Jumlah kalor yang dibutuhkan untuk menaikkan
suhu suatu benda sebesar 10C
Sifat khas suatu zat
T
Q
C


TcmQ 
T
Tmc
C



mcC 

34. Contoh 7
0,5 kg besi dinaikkan suhunya 30OC diperlukan
kalor 6750 joule, tentukan:
a. kapasitas kalor
b. kalor jenis
c. kalor yang dibutuhkan untuk menaikkan
suhunya sebesar 40OC
Diketahui
ΔT = 300C
c. Q? bila ΔT = 450C
m = 0.5 kg
Ditanya
Q = 6750 J
a. C?
b. c?

35. Penyelesaian
Contoh 7
CJ
T
Q
Ca 0
/225
30
6750
. 


ckg
J
m
C
c
mcCb
0
450
5.0
225
.


JQ
Q
TcmQc
9000
404505.0
.




36. HUBUNGAN KALOR & PERUBAHAN WUJUD ZAT
LmQ 
Q = Jumlah kalor yang diperlukan untuk mengubah
wujud suatu zat ( joule)
m = Massa zat (kg)
L = Kalor laten (joule/kg)
Pada perubahan wujud zat tidak terjadi perubahan suhu

37. Kalor Lebur (L)
Jumlah kalor yang dibutuhkan untuk mengubah
wujud 1 kg
Zat
kalor lebur (kJ/kg)
Lf
Kalor uap (kJ/kg)
LU
air 334 2256
alkohol 104 853
raksa 11,8 272
tembaga 134 5069
emas 64,5 1578
perak 88,3 2336
Sifat khas suatu zat

38. GAS
CAIR
Perubahan Wujud
PADAT
menyublim
medeposisi

39. Azas Black
“Bila sebuah sistem/benda melepas kalor
maka akan ada sistem/benda lain yang
menerima kalor dengan jumlah yang sama”
Qlepas = Qterima

40. Contoh 8
Diketahui
T1 = 280C
m1 = 200 g
Dua ratus gram air bersuhu 280C dicampur
dengan 20 gr air bersuhu 720C. Maka
suhu air campuran yang terjadi adalah…0C
(kalor jenis air 4200 J/kg0C)
T2 = 720C
m2 = 200 g
cair = 4200 J/kg0CQ (J)
T (0C)
28
72
TC
Q terima
Qlepas
ΔT1
ΔT2

41. Penyelesaian
Contoh 8
Diketahui
T1 = 280Cm1 = 200 g
T2 = 720Cm2 = 20 g
cair = 4200 J/kg0C
22 TcmQ airlepas 
11 TcmQ airterima 
1122 TcmTcm airair 
1122 TmTm 
   282007220  CC TT
: 20
   281072  CC TT

42. Contoh 8
   281072  CC TT
2801072  CC TT
CC TT 171028072 
CT11352 
CTC
0
32
11
352

Suhu akhir campuran adalah 320C

43. Contoh 9
Lima ratus gram air teh bersuhu 700C akan
dibuat es teh. Ketika sejumlah es bersuhu -50c
dicampurkan, ternyata hanya setengahnya
yang meleleh. Berapa banyak es yang
dicampurkan?
Q (J)
T (0C)
-5
70
T
Q terima
Qlepas
ΔT2
ΔT1
A
B C
D
Diketahui
T1 = 700C
m1 = 500 g
T2 = -50C
ces = 0,5 kal/g0C
cair = 1 kal/g0C
Lf = 80 kal/g0C

44. Contoh 9
Q (J)
T (0C)
-5
70
T
Q terima
Qlepas
ΔT2
ΔT1
A
B C
D
Diketahui
T1 = 700C
m1 = 500 g
T2 = -50C
ces = 0,5 kal/g0C
cair = 1 kal/g0C
Lf = 80 kal/g0C
11 TcmQ airterima 
Penyelesaian
BCABlepas QQQ 
 0701500 0

   fes LmTcm  22
1
22
     80505.0 22
1
2  mm
   22 405,2 mm  25,42 m
35000

45. Contoh 9
kalQterima 35000
25,42 mQlepas 
lepasterima QQ 
25,4235000 m
5,42
35000
2 m
gm 5,8232 
Banyaknya es yang dimasukkan adalah 823,5 g