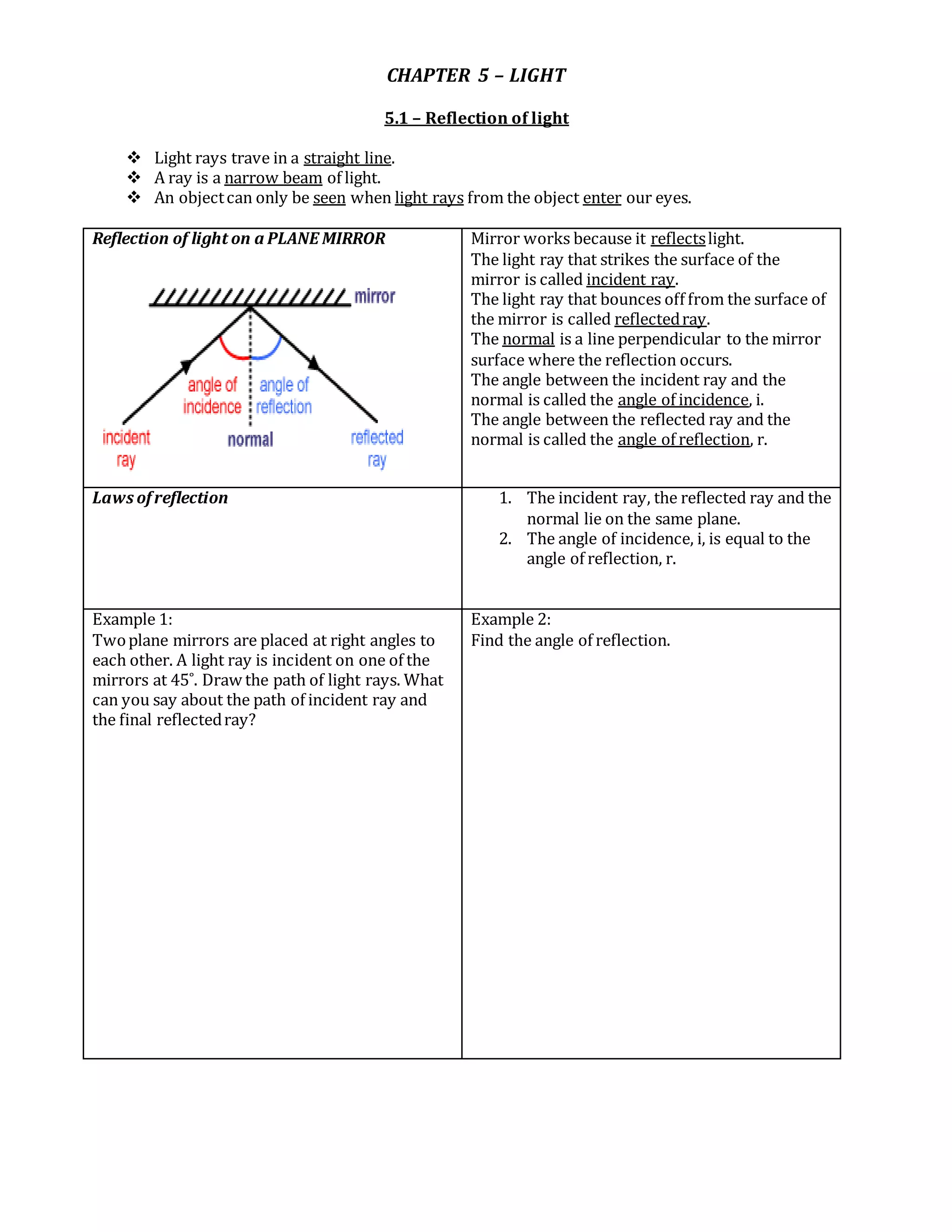
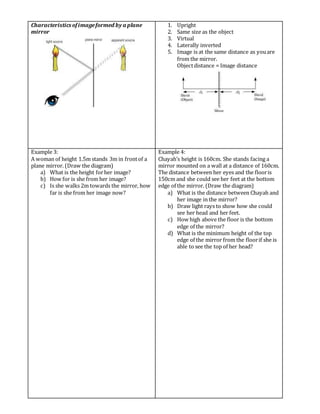
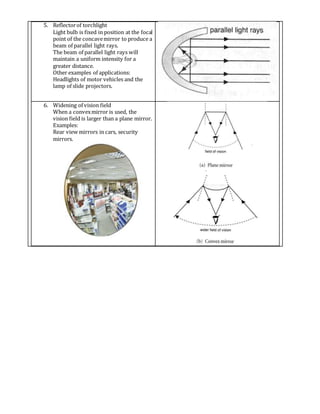
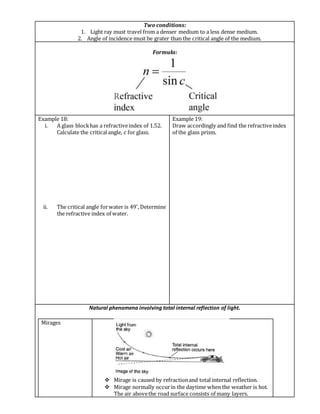
The document discusses the reflection and refraction of light. It defines reflection as light rays bouncing off a surface, while refraction is the bending of light rays when passing from one medium to another of different density. The key laws and concepts covered include: - The law of reflection, where the angle of incidence equals the angle of reflection - Refractive index, which indicates how much a medium bends light - Total internal reflection, which occurs when light travels from a dense to less dense medium at an angle greater than the critical angle Several examples and applications are provided, such as plane mirrors, mirages, fiber optics, and lenses. Convex lenses form real images while concave lenses form virtual, upright,

1. CHAPTER 5 – LIGHT
5.1 – Reflection of light
 Light rays trave in a straight line.
 A ray is a narrow beam of light.
 An objectcan only be seen when light rays from the object enter our eyes.
Reflection of light on a PLANE MIRROR Mirror works because it reflectslight.
The light ray that strikes the surface of the
mirror is called incident ray.
The light ray that bounces off from the surface of
the mirror is called reflectedray.
The normal is a line perpendicular to the mirror
surface where the reflection occurs.
The angle between the incident ray and the
normal is called the angle of incidence, i.
The angle between the reflected ray and the
normal is called the angle of reflection, r.
Laws ofreflection 1. The incident ray, the reflected ray and the
normal lie on the same plane.
2. The angle of incidence, i, is equal to the
angle of reflection, r.
Example 1:
Twoplane mirrors are placed at right angles to
each other. A light ray is incident on one of the
mirrors at 45˚. Draw the path of light rays. What
can you say about the path of incident ray and
the final reflectedray?
Example 2:
Find the angle of reflection.

2. Characteristics ofimageformed by a plane
mirror
1. Upright
2. Same size as the object
3. Virtual
4. Laterally inverted
5. Image is at the same distance as youare
from the mirror.
Objectdistance = Image distance
Example 3:
A woman of height 1.5m stands 3m in frontof a
plane mirror. (Draw the diagram)
a) What is the height forher image?
b) How for is she from her image?
c) Is she walks 2m towards the mirror, how
far is she from her image now?
Example 4:
Chayah’s height is 160cm. She stands facing a
mirror mounted on a wall at a distance of 160cm.
The distance between her eyes and the flooris
150cm and she could see her feet at the bottom
edge of the mirror. (Draw the diagram)
a) What is the distance between Chayah and
her image in the mirror?
b) Draw light rays to show how she could
see her head and her feet.
c) How high above the floor is the bottom
edge of the mirror?
d) What is the minimum height of the top
edge of the mirror from the floorif she is
able to see the top of her head?

3. Example 5:
A girl stands 4m in front of a mirror and a boy
stands 2m behind her. What is the distance
between the girl and the image of the boy. (Draw
the diagram)
Example 6:
A boy stands 5m in front of a plane mirror. If the
boy moves 2m forward.What is the distance
between the boy and his image now?(Draw the
diagram)
Curved mirrors
- a mirror with curved reflective surface
Principal axis A line passing through the vertex and the centre of curvature.
Centre of curvature, C The centre of the sphere that forms the curved mirror.
Radius of curvature,
CP
The radius of the sphere.
Focal point, F Concave mirror:
The point on the principal axis where all reflected rays converge and
meet.
Convex mirror:
The point on the principal axis where all the reflectedrays appear to
diverge from behind the mirror.
Focal length, f Distance between the focalpoint and the surface of the mirror.
Image distance, i Distance between the image and the surface of the mirror.
Objectdistance, u Distance between the object and the surface of the mirror.

4. Convex mirror Concave mirror
Drawing a ray diagram:
1. Draw a straight line as principal axis.
2. Draw a curvedline as the curved mirror and dotted vertical line at the vertex, P.
3. Mark position of F and C on the axis. CP=FP
4. Draw an arrow as the object standing upright on the axis at a given distance.
5. Draw ray P, ray F and ray C.
6. The top of the image is where any twoof the reflected rays meet after reflection.
7. Draw image.
CONCAVE MIRROR
Object
distance, u
Ray diagram Image
distance, v
Characteristics
Slightly
behind C
At C

5. Between C
and F
At F
Between F
and P
At infinity

6. CONVEX MIRROR
Object
distance, u
Ray diagram Image
distance, v
Characteristics
At infinity
At a distance
from the
mirror
At close
distance to
the mirror

7. APPLICATIONS OF REFLECTION OF LIGHT
1. Anti-parallax mirror in ammeters and
voltmeters.
A parallax error occurwhen youcan see
both the pointer and its image.
Our eyes must be normal to the pointer
when the image of the pointer cannot be
seen.
2. Periscope
Used to see over the top of high
obstacles such as a wall.
Also used in submarines to observe the
surrounding abovethe water.
Consist of 2 plane mirror inclined at 45˚.
Final image appears upright.
3. Ambulance
The word “AMBULANCE” is purposely
inverted laterally on an ambulance car.
Images seen throught the rear mirror of
a car is laterally inverted.
4. Make up mirror
Concave mirrors with long focallengths
can be used.
Images appear upright and magnified.

8. 5. Reflectorof torchlight
Light bulb is fixed in position at the focal
point of the concavemirror to produce a
beam of parallel light rays.
The beam of parallel light rays will
maintain a uniform intensity for a
greater distance.
Other examples of applications:
Headlights of motor vehicles and the
lamp of slide projectors.
6. Widening of vision field
When a convexmirror is used, the
vision field is larger than a plane mirror.
Examples:
Rear view mirrors in cars, security
mirrors.

9. 5.2 – Refraction of light
 Definition: The bending of light ray at the boundary as it travels from one medium to another
with different opticaldensities.
 It is due to a change in the velocity of light as it passes from one medium to another.
 The more optically dense a medium is, the slower light travels through it.
 A light ray travels much slower in a denser medium. The change in speed of light ray causes it to
change its direction.
When light ray travels from
less dense to a denser medium.
When light ray travels from a
denser to a less dense medium.
When light ray is incident
normally on the boundary
between the twomedium.
Laws ofrefraction 1. Incident ray, refracted ray and the normal lie in the same
plane.
2. The ratio of the sine of the angle of incidence, I to the sine
of angle of refraction, r is a constant.

10. Refractiveindex,n
 The value of the
constant for a light ray
passing through a
vacuum into a given
medium is called
refractiveindex.
 The is knownas
Snell’s law.
 Refractiveindex has
no unit.
 An indication of light-
bending ability of a
medium as light ray
enters its surface from
air/vacuum.
Formula:
A material with higher refractiveindex has a greater bending effect
on light as it slows downthe speed more. It causes a larger angle of
deviation of ray of light, dending the ray of light more towards the
normal.
Example 7:
Draw a figure showing the angle of incidence
on an air-water boundary of 50˚.
Calculate the angle of refraction, r if the
refrative index of water is 1.33.
Example 8:
Draw the diagram accordingly and determine the
refractiveindex of the glass.

11. Example 9:
Draw the diagram accordingly.
Refractiveindex of glass is 1.62.
What is the angle of incidence?
Example 10:
a) The speed of light passing through a
medium is 1.8x108 ms-1. Calculate the
refractiveindex of the medium.
b) What is the speed of light in a medium
with a refractiveindex of 2.4?
Example 11:
A light ray is incidently normal on a glass prism
that has refractiveindex of 1.50.
a) Complete the ray diagram.
b) Find the incident angle and the
refractiveangle.
Example 12:
A light ray travels from glass to air. Refractive
index of glass is 1.54 and speed of light in air is
3x108 ms-1.
Calculate:
a) The angle of refraction
b) Speed of light in glass

12. Phenomena due to refraction of light
Shallow swimming pool 1. Swimming pool appears to be shallower
than it really is.
2. Light rays frombottom of the pool is
refracted away from the normal as they
enter the air.
3. When lgiht rays reach the eye, they
appear to come from I, whichis higher
up.
4. Therefore, the pool appears to be
shallower.
Bent objectsin water 1. The pencil appears to be bent at the air-
water boundary.
2. Light rays fromthe end of pencil are
refracted at the air-water boundary and
bent away from the normal.
3. The image of the pencil under the water
appears to be higher than it really is.
4. Thus, the pencil appears bent at the
surface.
Fish-eye view 1. A fish or a diver can see objects above
the water surface, but the objects on the
shore wouldappear to be up in the air
at different positions.
Twinkling stars 1. Stars do not twinkle.
2. Light from the stars travel in straight
lines thorugh the vacuum of space.
3. When these light rays enter the earth’s
atmosphere, they are refracted by
layers of atmosphere of different
densities.
4. Densities of atmosphere layers are
constanly changing (due to wind and
temperature), thus altering the path of
the light rays.
5. One moment the light rays are refracted
in such a way that it reaches youreyes
and the next moment they are not.
6. Therefore, we see the stars twinkle.

13. REAL DEPTH
The distance of the real object, O from the
surface of water.
APPARENT DEPTH
The distance of the virtual imgae, I from the
surface of water.
Example 13:
A fish at the bottom of a pond appears to be
1.2m fromthe water surface, What is the depth
of the pond? (Refractiveindex of water=1.33)
Draw and answer.
Example 15:
A boy is standing inside a swimming pool. His legs
appead shorter when his friend observes him
from the pool side.
a) Explain how this phenomena happen.
b) Draw a ray diagram to show how his legs
appear shorter.
c) If the depth of the poolis 0.8m, calculate
the distance of the image of his feet as
seen from the surface of water. (n of
water=1.33)
Example 14:
Draw accordingly,and find the refractiveindex
of water.

14. Example 16:
An objectis placed under a glass block.The eye
of an observer is positioned at a distance of
10cm above the glass block.The image seen by
the observer is 12cm from the eye. If the
refractiveindex of the glass blockis 1.50, what
is the thickness of the glass block?
Example 17:
A glass blockwith length 18cm has refractive
index of 1.50. There is a bubble in the glass block.
When the bubble is seen from one side, it appears
at a distance of 8cm from that side.
When the bubble is seen from the opposite side, it
appears at a distance, d2. Determine the value of
d2.
5.3 – Total internal reflection of light
 Light ray bends away
from normal when it
travels through a denser
medium to a less dense
medium. Angle of
refraction is larger than
angle of incidence.
 When the angle of
incidence increases, the
angle of refraction also
increases.
 The refracted ray travels
along the glass-air
boundary.
 This is the limit of the
light ray that can be
refracted in air as the
angle in air cannot be any
larger than 90˚.
 The angle of incidence in
the denser medium at this
limit is called the critical
angle, c.
 If the angle of
incidence is increased
further so that it is
greater than the critical
angle, the light ray is
not refracted anymore
but is internally
reflected.
 This is called TOTAL
INTERNAL
REFLECTION.
Critical angle, c:
The angle of incidence in the denser medium when the angle of refraction, r in the less dense medium is
90˚.

15. Two conditions:
1. Light ray must travel from a denser medium to a less dense medium.
2. Angle of incidence must be grater than the critical angle of the medium.
Formula:
Example 18:
i. A glass blockhas a refractiveindex of 1.52.
Calculate the criticalangle, c for glass.
ii. The critical angle forwater is 49˚, Determine
the refractive index of water.
Example 19:
Draw accordingly and find the refractiveindex
of the glass prism.
Natural phenomena involving total internal reflection of light.
Mirages
 Mirage is caused by refractionand total internal reflection.
 Mirage normally occurin the daytime when the weather is hot.
The air abovethe road surface consists of many layers.

16.  The layers of air nearest the road are hot and the layers get
coolerand denser towards the upper layers.
 The refractiveindex of air depends on its density. The lower or
hotter layers have a lower refractiveindex than the layers
above them.
Rainbow
 A rainbow is formed by refraction,dispersion and total internal
reflection of light within water droplets.
 When sunlight shines on millions of water droplets in the air
during rain and after rain, we see a multicoloured arc.
 The colours run fromviolet along the lower part of the arc to
red along upper part of the arc.
 Light that forms the primary rainbow is first refracted and
dispersed in water droplets. Then, the light is reflected once
inside each water droplets. Finally the light is refractedand
dispersed again upon exiting the water droplet.
 This results in the light being spread out into a spectrum of
colour.
Applications of total internal reflection of light.
Prism periscope  Periscope is built using tworight-angled prisms.
 The critical angle of the glass prism is 42˚.
 Roral internal reflection occurswhen the light
rays strike the inside face of a 45˚ angles withan
angle of incidence greater than the criticalangle.
 Image produced is upright and has the same size
as the object.
Prism binoculars  A 45˚/45˚ prism can cause light rays to bend
through 180˚ when the light is incident at right
angles onto the hypotenuse of the prism.
 Light rays willbe totally reflected internally two
times in a pair of binoculars.
 Benefits:
o Image produced is upright.
o Distance between the objectivelens and
the eyepiece is reduced. This makes the
binoculars shorter as compared to a
teloscope.

17. Fibre Optics  An opticalfibre optic consists of an inner coreof
high refractiveindex glass and is surrounded by
an outer cladding of lower refractiveindex.
 When light in introduces into the inner core at
one end, it will propagate along the fibre in a
zigzag path undergoing a series of total internal
reflections.
 Optical fibres are useful forgetting light to
inaccesible places. For examples: as an endoscope
in medical field, as fibreoptic cables in
telecommunications.
 Advantage of fibreoptic cables over copper cables:
o Much thinner and lighter.
o Large number of signals can be sent
through at one time.
o Transmit signals with very little loss over
long distance.
o Signals are safe and free from electical
interference.
o Can carry large data forcomputers and
telecommunications.
5.4 – Lenses
Convex lenses Concave lenses
Convex lens Concave lens

18. Power of a lens:
Power = 1/f
Unit: Dioptre (D)
The shorter the focal length, the greater the power.
Power for convex lens in positive while power for concave lens in negative.
CONVEX LENS
Object
distance, u
Ray diagram Image
distance, v
Characteristics
At infinity
Beyond 2F
u>2f
At 2F
u=2f
Between 2F
and F
At F

19. Between F
and C
CONCAVE LENS
Image formed by concavelens is
always virtual, upright and
diminished.
Magnification 1. Size of image formed by a lens varies with the position of object.
2. Simplest way to compare the image witht the object is by the ratio of
their sizes.
3. Formula:
Example 20:
Draw accordingly and find the height of image.
Height of object is 5cm.
Example 21:
A convex lens forms an image of an object. If
the height of objectis 4cm, what is the height of
the image?
Lens formula:
f = focal length
u = object distance
v = image distance
Sign convention:
Distance Positivevalue
(+)
Negative value
(-)
u Real Virtual
v Real Virtual
f Convex lens Concave lens

20. Example 22:
An objectis placed in frontof a convexlens with a
focallength, f of 10cm. What are the characteristics of
the image formed if the objectdistance is 15cm?
Example 23:
An objectof height 6cm is places at a distance
of 20cm froma concavelens. Its focallength is
10cm. Find the position and size of the image.
Example 24:
A convex lens withfocallength 15cm formed an
image whichis real, inverted and same size with the
object. What is the objectdistance from the lens?
Example 25:
When an objectof height 3cm is placed 20cm
from a concavelens of focallength 30cm, what
is the height of the image formed?
Simple microscope 1. A magnifying glass is the simplest
microscope.
2. It consists of a single convexlens with
short focal length.
3. When the magnifying glass is held near
to the eye and the objectis placed
inside its focallength (u<f),a virtual,
magnified and upright image is formed.

21. Compound microscope 1. To view very small objects like
microorganisms.
2. 2 powerful conveslenses of short focal
lengths:
a. Objectivelens
b. Eyepiecelens
3. Focal length for objectivelens is shorter
than focallength foreyepiece lens.
(fo<fe)
4. Objectto be observed must be plaved
between Fo and 2Fo.
5. 1st image: Real, inverted and magnified
6. Eyepiecelens is used as magnifying
glass to magnify the first image.
7. Eyepiecelens must be positioned so
that the first image is between the lens
and Fe
8. 2nd image: Virtual, upright, magnified.
9. In normal adjustment, distance
between the lenses is greater than the
sum of their individual focal length
(L>fo+fe)
10. Magnification of a compound
microscope:
m = mo x me
Teloscope 1. To view distant objects like stars.
2. 2 convex lenses:
a. Objectivelens
b. Eyepiecelens
3. fo > fe
4. Objectivelens converges the parallel
rays from a distant object and forms a
real, inverted and diminised image at
its focalpoint.
5. Eyepiecelens is used as a magnifying
glass to form a virtual, upright and
magnifies image.
6. At normal adjustment, final image is
formed at infinity.
7. This is done ny adjusting the position of
the eyepiece lens so that the first real
image becomes the objectat the focal
point of the eyepiece lens.
8. Normal adjustment: Distance between
lenses = fo + fe .