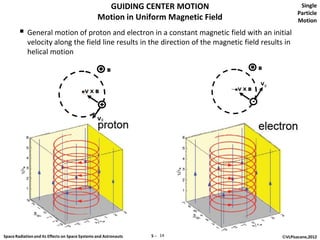
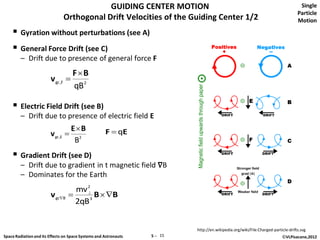
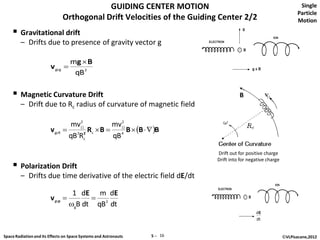
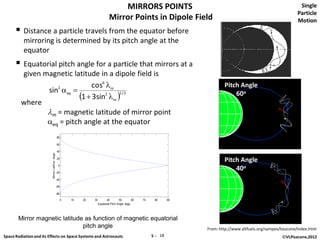
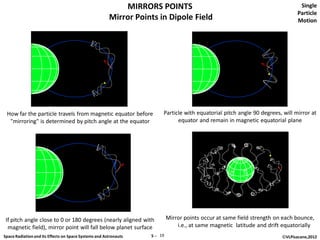
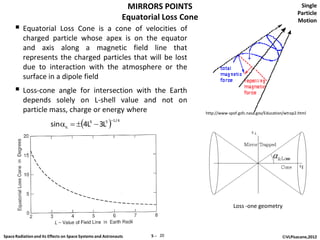
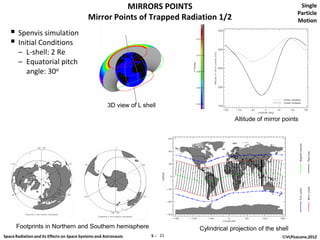
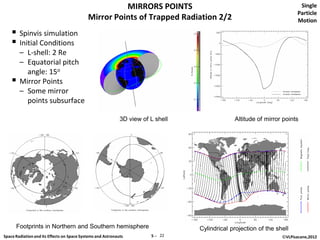
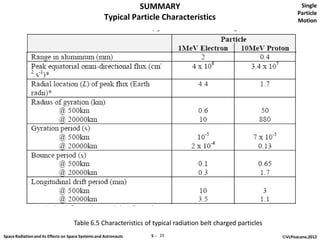
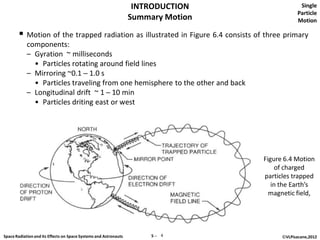
The document discusses space radiation and its effects on both space systems and astronauts, focusing on the motion of charged particles in magnetic fields. Key topics include gyration motion, guiding center motion, and mirror points, explaining how charged particles behave under the influence of electromagnetic forces. It also presents equations of motion, gyro-frequency, and the parameters governing particle movements in magnetic fields.









![GYRATION MOTION Single
Particle
Larmor Radii and Gyro-frequency in Terms of Magnetic rigidity Motion
Examples of Larmor radii and gyro-frequency for any charged particle with a given
rigidity at
Sun
near Earth
surface of the Earth
Larmor Radius, Re = Earth radii
Magnetic Kinetic Speed
Rigidity Energy [% of c] Corona Interplanetary Earth
(10 mT) 1 AU (5 nT) Surface (30 μT)
1 GV 0.43 GeV 73% 330 m 6.6x108 m ≈ 100 Re 1.1x105 m ≈ 0.017 Re
5 GV 4.1 GeV 98% 1.65 km 3.3x109 m ≈ 520 Re 5.5x105 m ≈ 0.086 Re
20 GV 19.1 GeV 99.8% 6.60 km 1.3x1010 m ≈ 2100 Re 2.2x106 m ≈ 0.340 Re
Gyro-frequency
Magnetic Kinetic Speed
Rigidity Energy [% of c] Corona Interplanetary Earth
(10 mT) 1 AU (5 nT) Surface (30 μT)
1 GV 0.43 GeV 73% 105.6 kHz 0.053 Hz 316.9 Hz
5 GV 4.1 GeV 98% 28.4 kHz 0.142 Hz 85.1 Hz
20 GV 19.1 GeV 99.8% 7.2 kHz 0.004 Hz 21.7 Hz
Space Radiation and its Effects on Space Systems and Astronauts 5 ─ 10 ©VLPisacane,2012](https://image.slidesharecdn.com/spaceradiationandeffectsonspacesystemsastronautscoursesampler-120524092136-phpapp01/85/Space-Radiation-It-s-Effects-On-Space-Systems-Astronauts-Course-Sampler-11-320.jpg)