This document provides information on Henry's law and its applications. It discusses how Henry's law states that the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas. Raoult's law is introduced as a special case of Henry's law that applies to solutions of volatile liquids. Characteristics of the Henry's law constant KH and examples of applying Henry's law such as carbonation of soft drinks are provided. The document also covers ideal and non-ideal solutions, azeotropes, and colligative properties.

1. 1
SOLUTIONS
~ BHARTI SINGH
Chemistry Lecturer
S.D.Public School
Class 12th

2. TOPICS
1. Henry’s law [solubility of gas in a liquid].
2. Characteristics of K H .
3. Applications of Henry’s law.
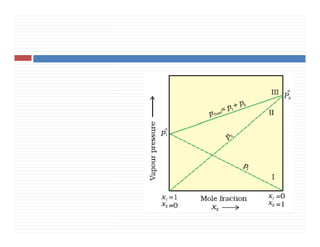
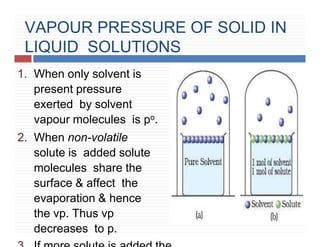
4. Raoult’s law for volatile liquids & for non volatile
solutes.
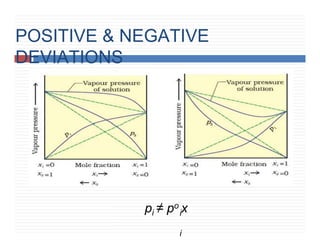
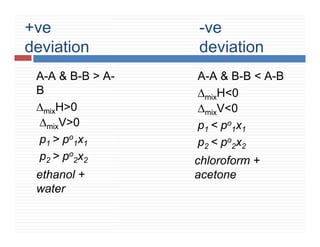
5. Ideal & non ideal solution
6. Colligative properties – Relative lowering of vapour
pressure.

3. HENRY’S
LAW
H
“The solubility of a gas in a liquid is directly proportional
to the pressure of the gas.” (S α p)
Dalton’s Law: the solubility of a gas in a liquid solution is a
function of partial pressure of the gas. (S α p)
In other words:
“mole fraction of gas in the solution is proportional to the
partial pressure of the gas over the solution” (χ α p)
Most commonly used Henry’s Law:
“the partial pressure of the gas in vapour phase (p)
is proportional to the mole fraction of the gas (x)
in the solution”
and is expressed as: p= KH . X

4. Characteristics of
KH
1. KH value depends upon Nature of gas, P & T.
2. Different gases → different KH values at the same T .
3. ↑ the KH at a given P, ↓ is the S. (KH α 1/S)
4. ↑ the T, ↑ is KH & thus ↓ the S.
(aquatic species are more comfortable in cold water than hot
water)

5. APPLICATIONS OF HENRY’S
LAW
1. S of CO2 in soft drinks and soda
water
2. Scuba divers → bends
3. At high altitudes → anoxia

6. VAPOUR PRESSURE OF LIQUID
SOLUTIONS
1. Vapour pressure of liquid-liquid solutions
2. Raoult’s law as special case of Henry’s law
3. Vapour pressure of liquid-solid solutions

7. VAPOUR PRESSURE OF LIQUID-
LIQUID SOLUTIONS
⮚ Raoult’s law which states that for a solution of volatile liquids
the partial vapour pressure of each component in the
solution is directly proportional to its mole fraction.
⮚ For a solution containing two liquids 1 & 2…
∴ p1 = po
x
1
1
∴ p2 = po
x
2
2
p1 ∝ x1
similarly, p2 ∝ x2
where,
p1 & p2 are partial pressures of comp. 1 &
2 in the solution
po o
1 &p 2 are partial pressures of pure
components 1 & 2
x1 & x2 are mole fractions of 1 & 2 in the
solution.

8. Now, according to Dalton’s law of partial
pressures..ptotal
=p1
+ p2
= po
1 x1 + po
2 x2
= po
1 (1-x2) + po
2 x2
= po
1 + (po
2 - po
1)x2
Conclusions….
1. ptotal can be related to the x or any one component.
2. ptotal over the solution ∝ x2 .
3. Depending on the po
1 & po
2 , ptotal decreases or
increases
with the increase of
the x
1 .

10. COMPOSTION IN THE VAPOUR
PHASE
⮚ The composition of vapour phase in equilibrium
with the solution is determined by the partial
pressures of the components.
⮚ If y1 and y2 are the mole fractions of the components
1 and 2 respectively in the vapour phase then,
using Dalton’s law of partial pressures:
p1
= y1
ptotal
p2
= y2
ptotal
In general,
pi
= yi
ptotal

11. RAOULT’S LAW AS A SPECIAL
CASE OF HENRY’S LAW
Raoult’s law: pi = po
i xi
Henry’s law: pi = KHxi
⮚ In the solution of a gas in a liquid, when one of the
components is so volatile that it exists as a gas, it
Raoult’s law becomes a special case of Henry’s
law.
o
⮚ Comparing the two equations: p i is similar
to KH.

12. VAPOUR PRESSURE OF SOLID IN
LIQUID SOLUTIONS
1. When only solvent is
present pressure
exerted by solvent
vapour molecules is po.
2. When non-volatile
solute is added solute
molecules share the
surface & affect the
evaporation & hence
the vp. Thus vp
decreases to p.

13. RAOULT’S LAW FOR S IN L
SOLUTIONS
“For any solution the partial
vapour pressure of each
volatile component in the
solution is directly
proportional to its mole
fraction.”
p1 ∝ x1
p1 = po
1x1

14. Raoult’s law for solution of solids in
liquids
The relative lowering of vapor pressure of a solution containing a
non-volatile solute is equal to the mole fraction of the solute in the
solution.
P º - P = x B = W 2 X M 1
P º W 1 X M 2
W 2 , M2 = mass in gram and molecular mass of solute
W1 , M1 = mass in gram and molecular mass of solvent
P º = vapor pressure of pure solvent
P = vapor pressure of pure solution
x B = mole fraction of solute

15. IDEAL & NON-IDEAL SOLUTIONS
Liquid-liquid solutions on the basis of Raoult’s law
can be classified into…
1. Ideal solutions &
2. Non-ideal solutions.

16. IDEAL SOLUTIONS
Ideal solutions: The solutions which obey Raoult’s
law over the entire range of concentration
,temperature and pressure are known as ideal
solutions.
Ideal solutions have two important properties:
1. Enthalpy of mixing ∆mixH=0 (i.e. no heat change
occurs on mixing)
2. Volume of mixing ∆mixV=0 (i.e. vol. of solution is
equal to sum of volumes of two liquids exactly)

17. Elaboratio
n..
Consider two liquids A & B:
1. Intermolecular forces of attraction in pure
components will be A-A & B-B.
2. In the solution, IMF would be A-B
3. If A-A & B-B are nearly equal to A-B, ideal
solution is formed.
4. A perfectly ideal solution is rare.
5. Examples: n-hexane & n-heptane, benzene &
toluene, bromoethane & chloroethane are nearly
ideal solutions.

18. NON-IDEAL SOLUTIONS
“When a solution does not obey Raoult’s law over the
entire range of concentration, then it is called non-
ideal solution.”
⮚ Thus the vp is either higher (+ve deviation) or
lower (-ve deviation) contrary to as expected
Raoult’s law.

19. POSITIVE & NEGATIVE
DEVIATIONS
pi ≠ po x
i
i

20. +ve
deviation
-ve
deviation
A-A & B-B > A-
B
∆mixH>0
∆mixV>0
p1 > po
1x1
p2 > po
2x2
ethanol +
water
A-A & B-B < A-B
∆mixH<0
∆mixV<0
p1 < po
1x1
p2 < po
2x2
chloroform +
acetone

21. AZEOTROPE
S
“Some liquids on mixing, form azeotropes which are
binary mixtures having the same composition in
liquid and vapour phase and boil at a constant
temperature.
⮚ the components cannot be separated by fractional
distillation.
⮚ There are two types of azeotropes
Minimum boiling azeotrope
(ethanol+water : approximately 95% by volume of
ethanol)
and
Maximum boiling azeotrope

22. COLLIGATIVE PROPERTIES
Vapour pressure of a solvent decreases when
a non- volatile solute is added.
(1) Relative lowering of vapour pressure of the
solvent
(2) Depression of freezing point of the solvent
(3) Elevation of boiling point of the solvent and
(4) Osmotic pressure of the solution.
“The properties which depend on the number of
solute particles irrespective of their nature
relative to the total number of particles present
in the solution are called “Colligative
properties.”

23. 1. RELATIVE LOWERING OF
VP

24. THANK
YOU