The document provides an overview of basic probability concepts, including definitions, laws, and types of events such as independent, dependent, and conditional events. It explains various probability calculations, including a priori and conditional probabilities, and discusses the application of Bayes' theorem. It also covers concepts such as joint and marginal probabilities, as well as the relationships between events in probability.






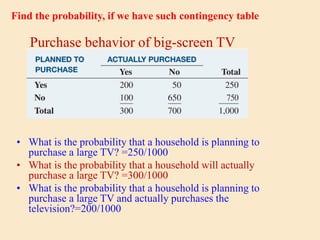

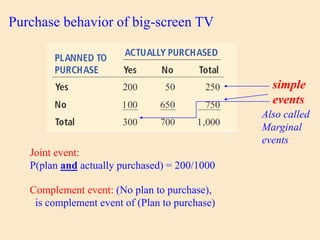

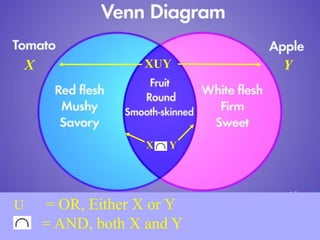



![Example: Law of Addition [ X OR Y ]](https://image.slidesharecdn.com/slide2basicprobability-240508154410-da361adf/85/Slide-2-Basic-probabilityjhhhhhhhhhhh-pdf-15-320.jpg)











