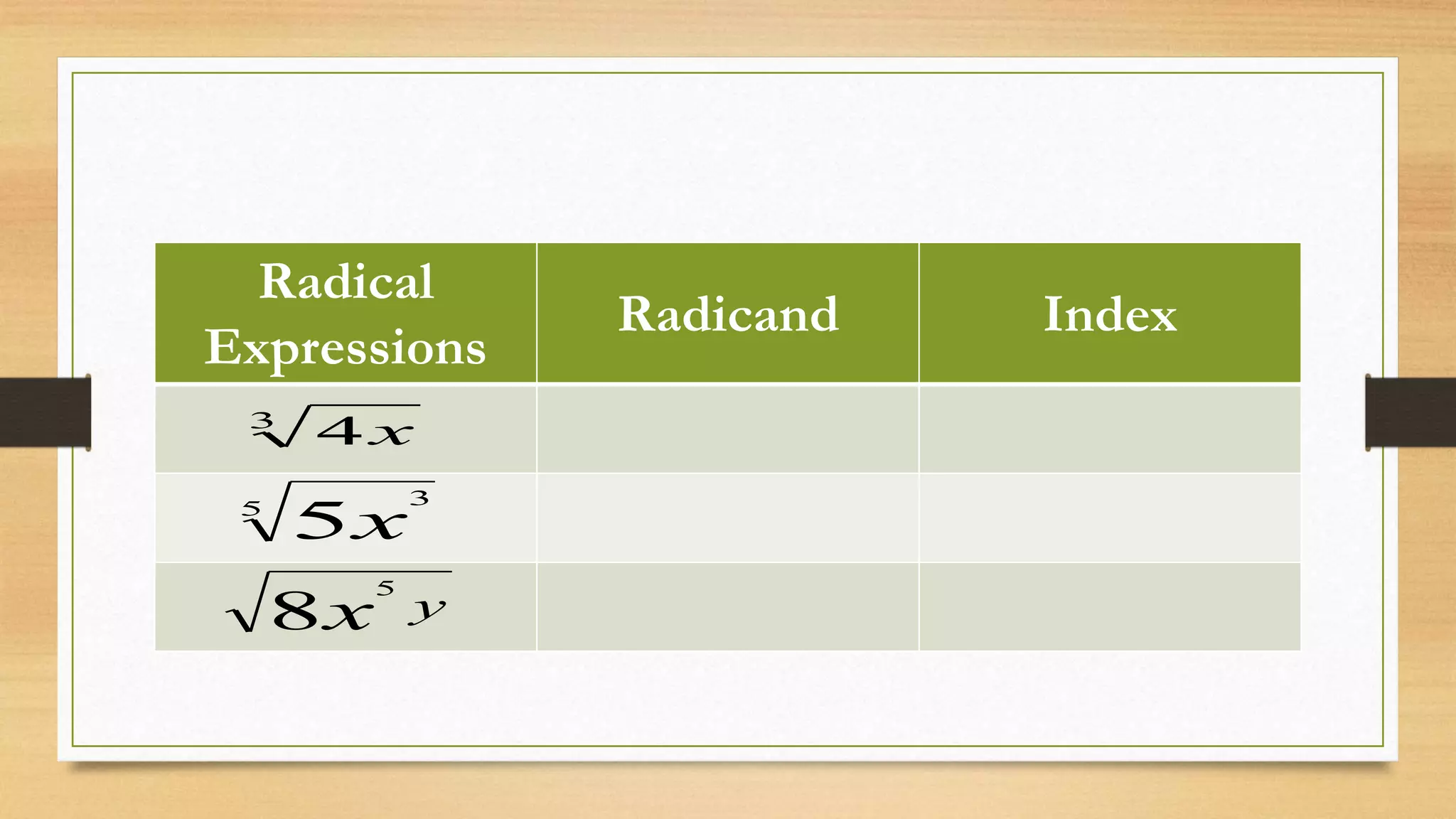
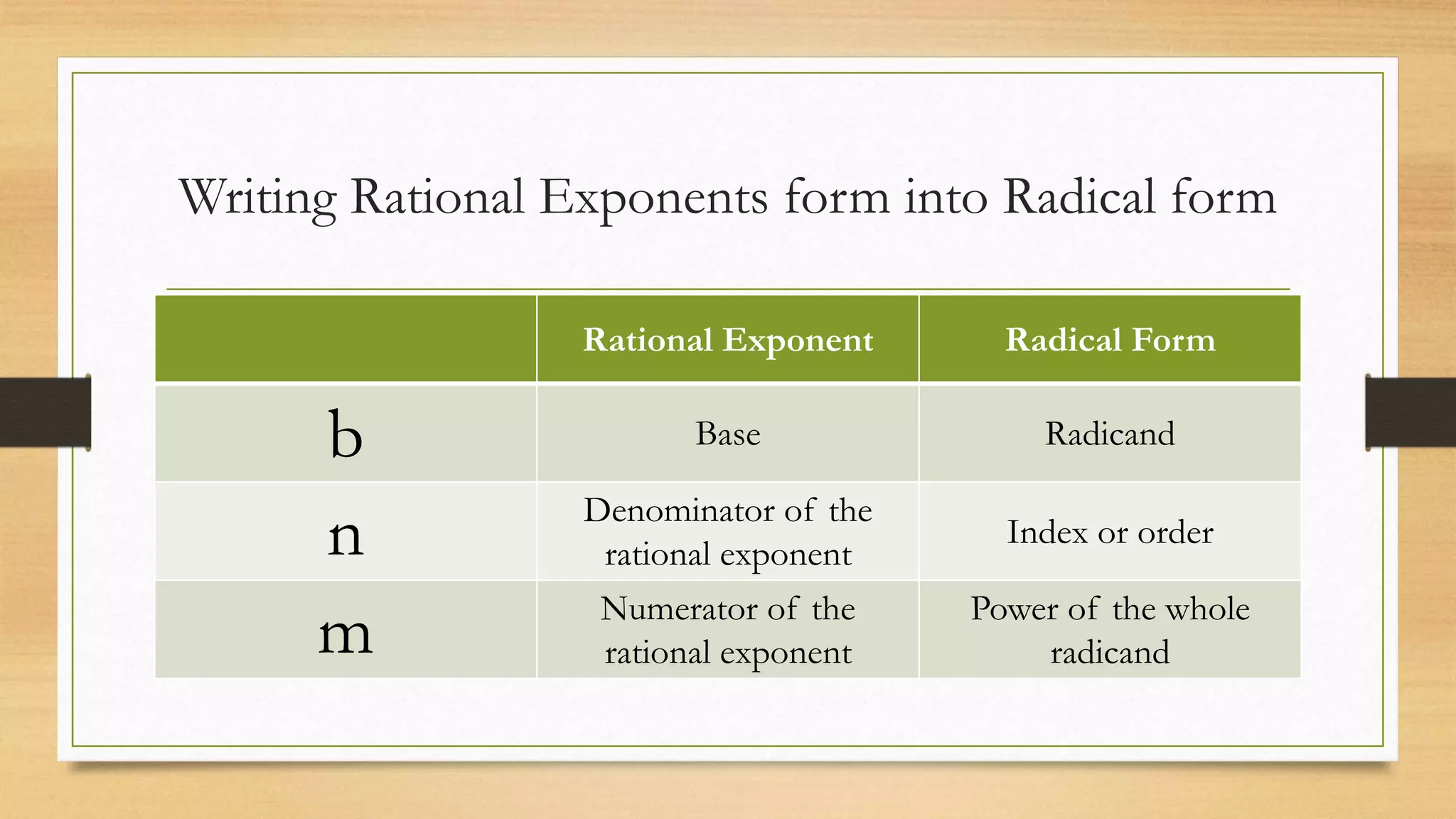
This document provides an overview of radical functions including:
- Definitions of nth roots and the principal nth root
- Converting between rational exponents and radical form
- Laws of radicals for addition, subtraction, multiplication, and division
- Simplifying radicals by removing factors from the radicand or reducing indices
- Rationalizing denominators containing radicals by using conjugates