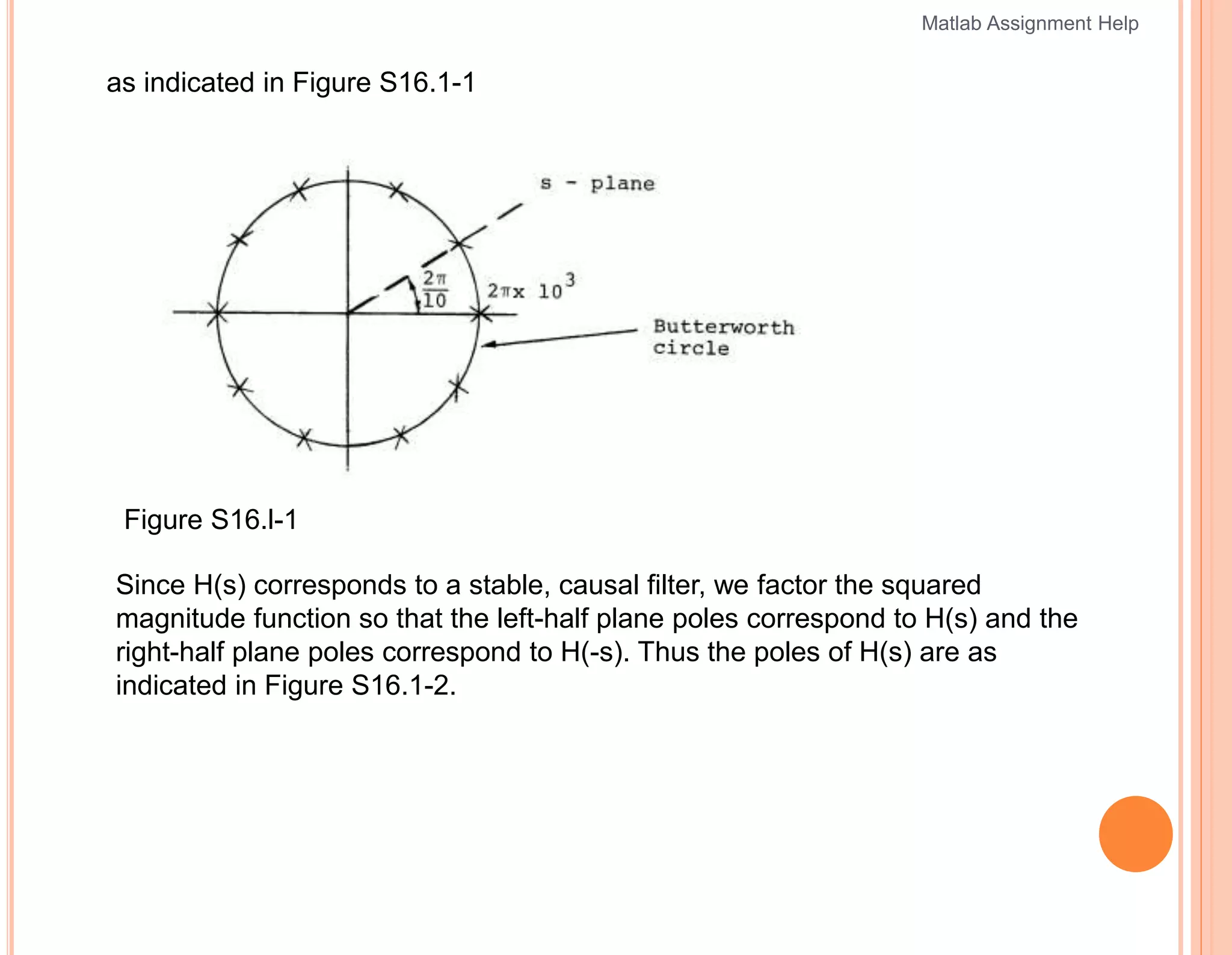
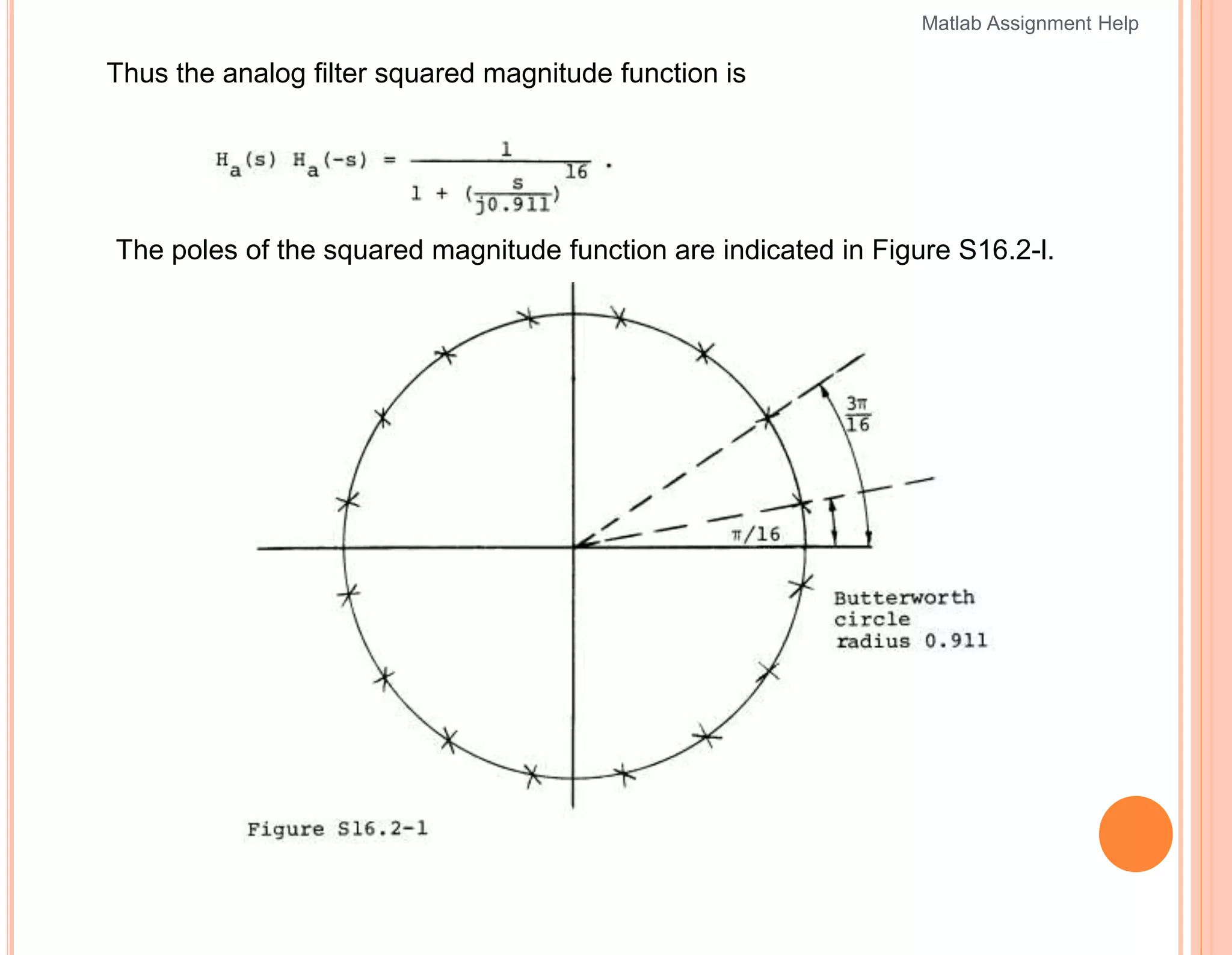
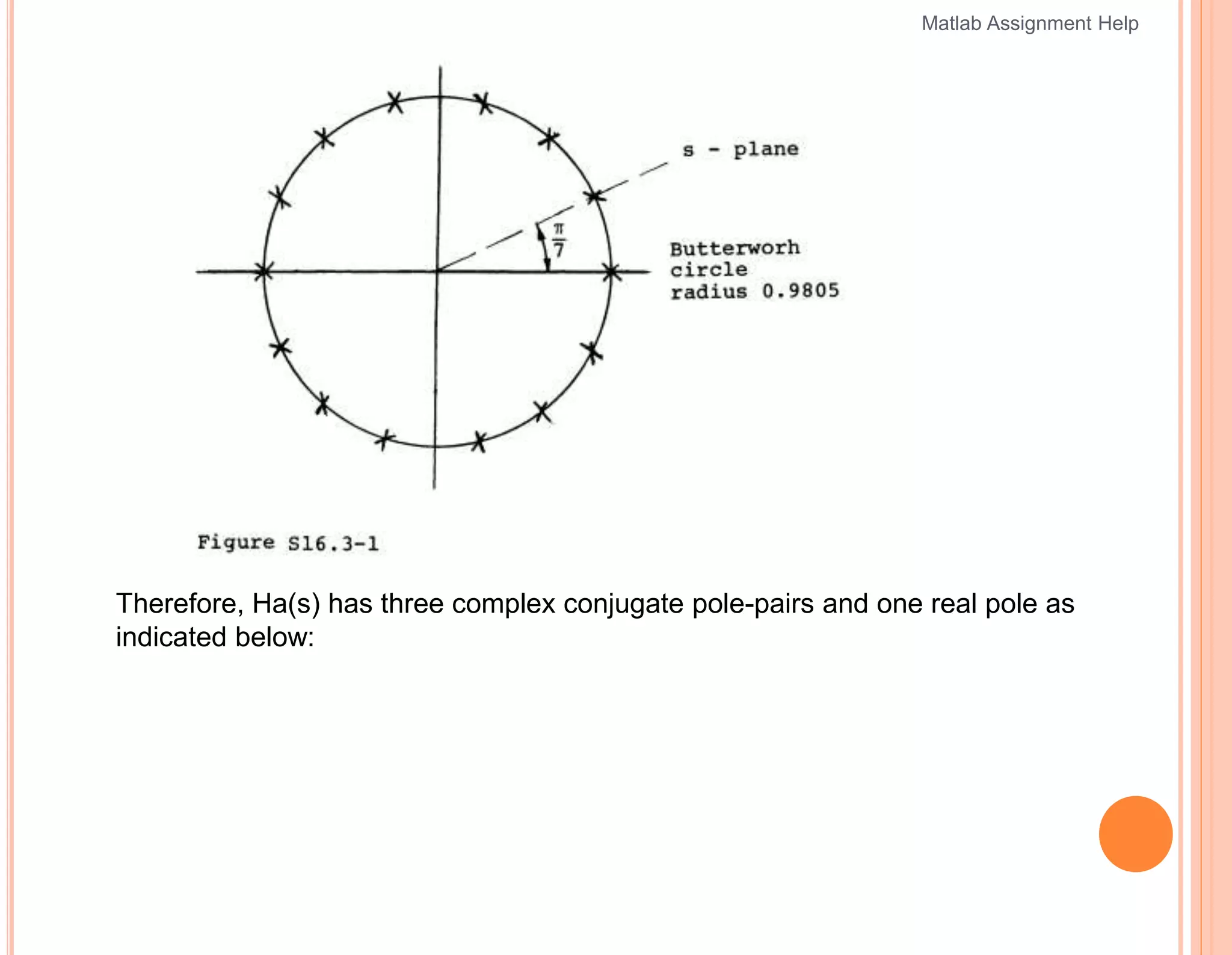
The document outlines a series of problems related to digital signal processing and filter design, particularly focusing on Butterworth filters. It includes specifications for analog and digital filters, methods for determining pole locations, and transformations between filter types. Additionally, it provides solutions for designing a lowpass filter and converting it to a highpass filter using specific transformations.