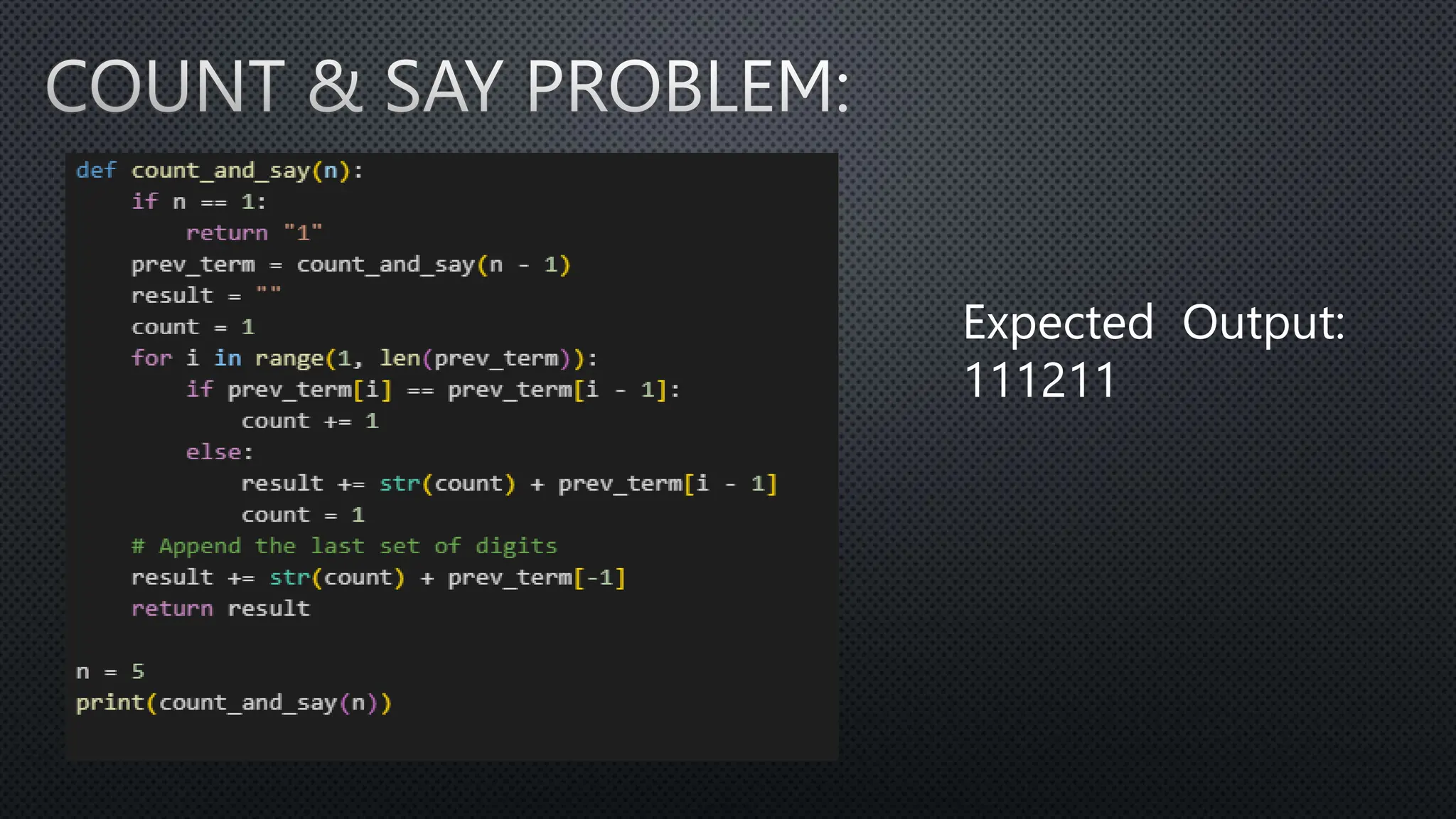
This document discusses sets in Python. It explains how to create a set using curly braces or the set() constructor, add elements using the add() method, and remove elements using the remove() or discard() method. It also describes set operations like union using |, intersection using &, difference using -, and symmetric difference using ^. Finally, it briefly mentions set comprehensions which are similar to list comprehensions but use curly brackets.

2. Creating a set
Adding elements to set
Removing elements
Union |
Intersection &
Difference –
Symmetric difference ^
Set comprenshive

3. Creating a set
• You can create a set using curly braces {} or the set() constructor.
• Sets are used to store multiple items in a single variable.
• It is a collection which is unordered, unchangeable*, and unindexed

4. Adding the elements
You can add elements to a set using the add()
method:

5. Removing the elements
You can remove elements from a set using the remove() or discard()
method:

6. Union (|)
You can perform a union operation to combine two sets into one, without
duplicates, using the union() method or the | operator:

7. Intersection (&)
You can find the common elements between two sets using the
intersection() method or the & operator:

8. Difference(-)
The difference between two sets A and B include elements of set A that are not present
on set B using the difference() method or the – operator.

9. Symmetric Difference(-)
Set Symmetric Difference The symmetric difference between two
sets A and B includes all elements of A and B without the common
elements using the symmetric_difference() method or the ^
operator:

10. Set comprenshive
Set comprehensions are pretty similar to list comprehensions. The only difference
between them is that set comprehensions use curly brackets { }

11.  The Dutch National Flag problem, also known
as the Three-Way Partitioning problem, is a
famous computer science problem related to
sorting an array of elements containing three
distinct values (usually represented as 0, 1, and
2) in a specific order.
 Here's a Python program that solves the Dutch
National Flag problem using the "Dutch
National Flag Algorithm":

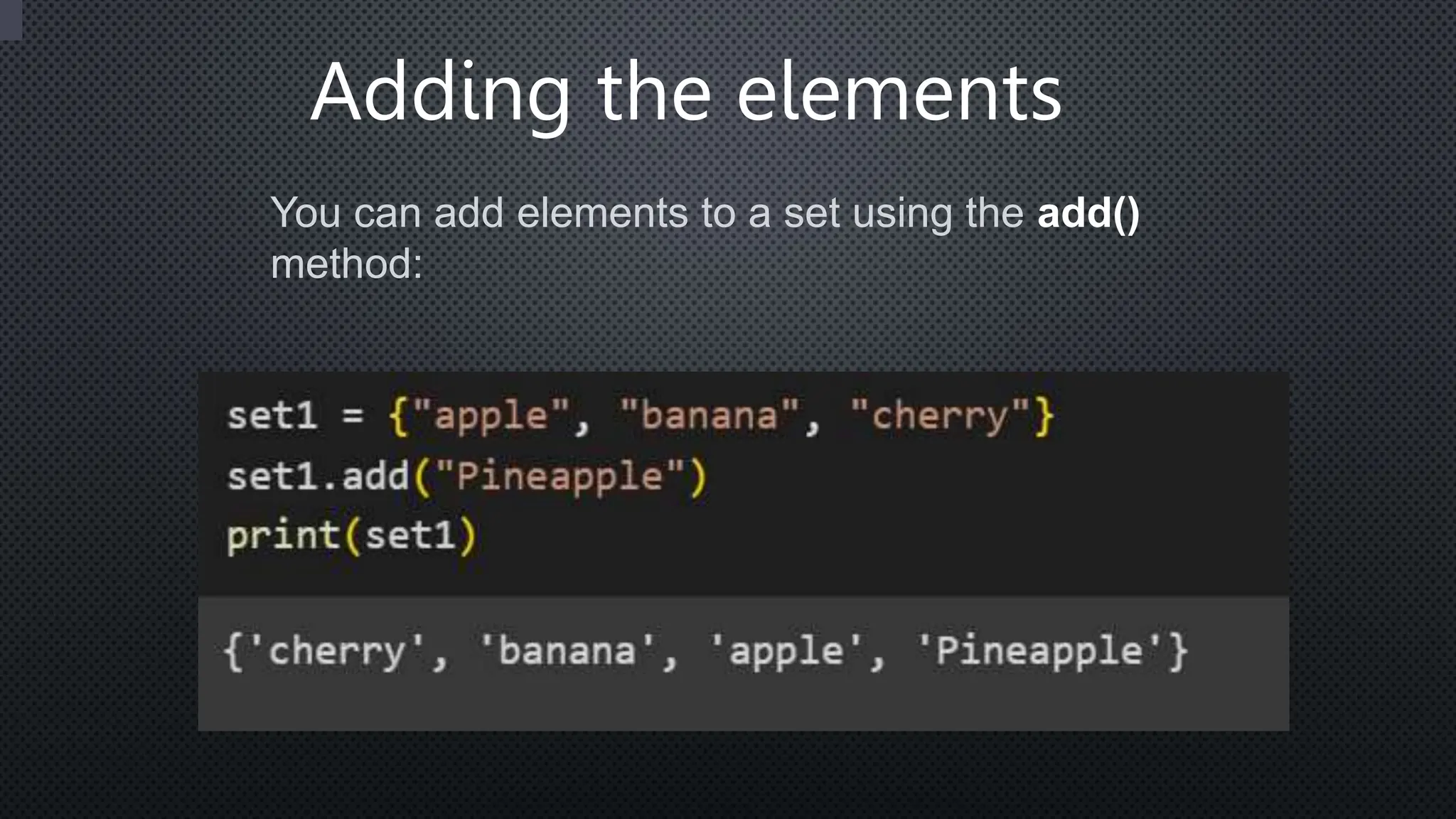
12. Expected Output:
[0,0,1,1,2]

13. The Count and Say problem is a
sequence generation problem. Given
an integer n, the task is to generate the
nth term of the "Count and Say"
sequence.
The sequence starts with "1", and each
subsequent term is obtained by reading
the previous term aloud and counting
the number of digits of the same type in
a row.

14. Expected Output:
111211