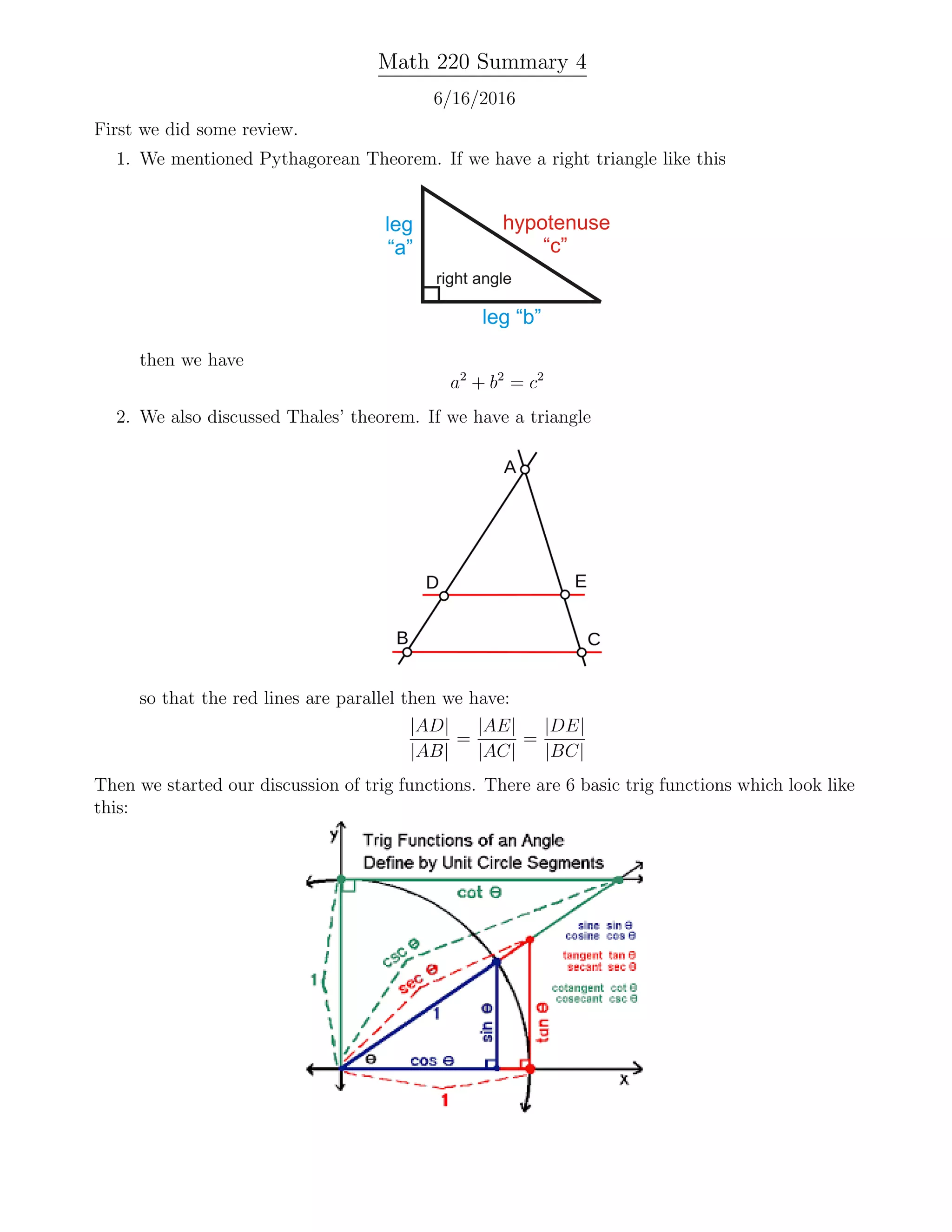
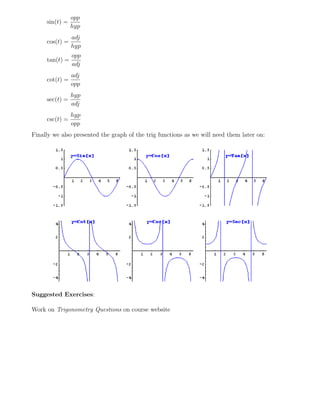
The document summarizes key topics covered in a Math 220 class, including a review of Pythagorean theorem and Thales' theorem. It then introduces the six basic trigonometric functions of sine, cosine, tangent, cotangent, secant, and cosecant. Various angle relationships for these trig functions are also defined, along with recommended values to memorize for specific angles. Finally, the document defines the trig functions in terms of right triangles with non-unit hypotenuses and provides a graph of the trig functions.

1. Math 220 Summary 4
6/16/2016
First we did some review.
1. We mentioned Pythagorean Theorem. If we have a right triangle like this
then we have
a2
+ b2
= c2
2. We also discussed Thales’ theorem. If we have a triangle
so that the red lines are parallel then we have:
|AD|
|AB|
=
|AE|
|AC|
=
|DE|
|BC|
Then we started our discussion of trig functions. There are 6 basic trig functions which look like
this:

2. This gives us the following relations:
1. sin2
(t) + cos2
(t) = 1
2. tan2
(t) + 1 = sec2
(t)
3. 1 + csc2
(t) = csc2
(t)
4. tan(t) =
sin(t)
cos(t)
5. cot(t) =
cos(t)
sin(t)
6. sec(t) =
1
cos(t)
7. csc(t) =
1
sin(t)
Also we can get the following angle relations:
1. sin(t + 2π) = sin(t) and cos(t + 2π) = cos(t)
2. sin(−t) = − sin(t) and cos(−t) = cos(t)
3. sin(t + π) = − sin(t) and cos(t + π) = − cos(t)
4. sin(π
2
− t) = cos(t) and cos(π
2
− t) = sin(t)
Because of the angle relaction it suffices to memorize sin and cos for the following angles and
deduce the rest if need be.
1. t = 0 : sin(0) = 0 & cos(0) = 1
2. t =
π
6
: sin(
π
6
) =
1
2
& cos(
π
6
) =
√
3
2
3. t =
π
4
: sin(
π
4
) =
√
2
2
& cos(
π
4
) =
√
2
2
4. t =
π
3
: sin(
π
3
) =
√
3
2
& cos(
π
3
) =
1
2
5. t =
π
2
: sin(
π
2
) = 1 & cos(
π
2
) = 0
We also discussed what happens when the hypotenuse is not the unit like in this picture:
Then we have the following relations

3. sin(t) =
opp
hyp
cos(t) =
adj
hyp
tan(t) =
opp
adj
cot(t) =
adj
opp
sec(t) =
hyp
adj
csc(t) =
hyp
opp
Finally we also presented the graph of the trig functions as we will need them later on:
Suggested Exercises:
Work on Trigonometry Questions on course website