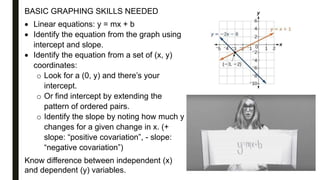
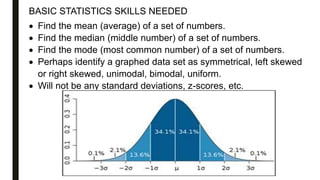
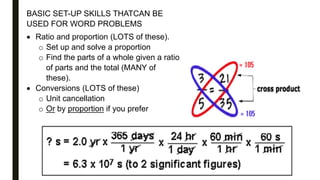
The math section of the TEAS test contains 36 multiple choice questions to be completed within 54 minutes, covering topics such as arithmetic, algebra, statistics, and word problems. Test takers should review basic math skills like operations with fractions, algebraic equation solving, linear graphing, and strategies for setting up and solving word problems. Preparing for the math portion requires practicing these fundamental math skills as well as taking full-length practice tests to experience the pacing.

1. CONQUERING THE TEAS
Part 3:
Math Test

2. THE MATH TEST
 36 questions in 54 minutes: that’s 1 ½ minutes
per question.
 Each problem is stand alone.
 About 25% of the questions are arithmetic and
algebra problems.
 About 15%, although not true “word problems,”
are more than arithmetic, using tables or
graphs (mostly the coordinate system).
 About 60% are true “word problems”. So need
to practice word problems along with your
basic arithmetic and algebra skills.
 All questions are multiple choice.
 Preparation:
o Review basic math skills.
o Take practice tests.

3. MULTIPLE CHOICE STRATEGIES USUALLY
IRRELEVANT
 Because a math problem has a number answer
and so the choices are all numbers!
 So you have to do the problem, get the answer
and make the choice.
 Sometimes you can still use the procedure of
going through the choices one by one and
eliminating incorrect answers until you find the
correct one.
o This usually happens in a linear equation
problem:
 Find the y-intercept and eliminate those
that don’t have it.
 Then use slope to choose between the
remaining possibilities

4. o Very rarely a question might have word answers: One example
is “What is the result of dividing a positive integer X by a
positive number less than 1?” (two answers can be eliminated)
 A number greater than X
 A number less than X
 A negative number (may be eliminated: +/+ = +)
 An irrational number (eliminate: only a result of square
root)

5. BASIC MATH SKILLS NEEDED
 Operations with fractions
 Interchange between fractions,
decimals and percents (lots of
these)
 Operations with signed numbers
(integers)
 Find greatest common factor (GCF)
 Find least common multiple (LCM)
 Order of operations (PEMDAS)

6.  Arrange numbers from small to large (a list with positive numbers, negative
numbers, fractions and decimals, even square roots).
 Place value and rounding (for MOST problems: you pick the closest answer!)
 Some basic geometric formulas.
 A few basic conversion facts
o METRIC
o English
 Probably at least one scientific notation problem

7. BASIC ALGEBRA SKILLS NEEDED
 Change simple word statements into symbolic
expressions/equations.
 Evaluate an algebraic expression given value(s) to
substitute.
 Solve basic equations/inequalities.
o Combine like terms.
o Pull out GCF or distribute to remove parentheses
o Do the same thing to both sides to isolate the
variable:
 Add/subtract
 Multiply/divide
 Multiply fractional coefficients by reciprocal.
 Cross multiply in the case of a proportion.
 Be able to FOIL two binomials.

8. BASIC GRAPHING SKILLS NEEDED
 Linear equations: y = mx + b
 Identify the equation from the graph using
intercept and slope.
 Identify the equation from a set of (x, y)
coordinates:
o Look for a (0, y) and there’s your
intercept.
o Or find intercept by extending the
pattern of ordered pairs.
o Identify the slope by noting how much y
changes for a given change in x. (+
slope: “positive covariation”, - slope:
“negative covariation”)
Know difference between independent (x)
and dependent (y) variables.

9. BASIC STATISTICS SKILLS NEEDED
 Find the mean (average) of a set of numbers.
 Find the median (middle number) of a set of numbers.
 Find the mode (most common number) of a set of numbers.
 Perhaps identify a graphed data set as symmetrical, left skewed
or right skewed, unimodal, bimodal, uniform.
 Will not be any standard deviations, z-scores, etc.

10. WORD PROBLEMS: BASICS
 What is a word problem?
o Most math problems give the “set-up”: you just
do the mechanics of evaluating (expressions) or
solving (equations).
o A word problem makes you:
 READ
 THINK
 Come up with the expression or equation
(the HARD part).
 Then of course do the straightforward
mechanics of evaluating or solving (the
EASY part).
 It doesn’t tell you what to do. Once you accept
responsibility of thinking it out for yourself:
AMAZING, IT IS POSSIBLE, THESE CAN BE
DONE!

11. HOW TO DO A WORD PROBLEM
 Read the problem.
 What is being asked for? (usually one or two answers).
o Assign an algebraic expression to each answer being asked for
using the given relationship between them (e.g. “a number” = “x” and “5
more than the number” = “x + 5”).
o Write an equation with those algebraic expressions in it
 Often it’s just add the expressions and set them equal to a value
actually given in the problem (think: how would anyone calculate that
given value? – the equation is that calculation).
$10000 in two accounts, one 2.5%, the other 5%, total interest = $300
Interest in 2.5% account + interest in 5% account = total interest
.025x + .05(10000 – x) = 300

12.  Now solve the equation for
x: this is just mechanical,
like any problem that gives
you the set-up, only you
came up with this set-up!
o“x” = something and that
is one of the answers.
oIn the above example,
subtract that from 10,000
to get the other answer
(“10,000 - x”).

13. NOTE: SOME “WORD” PROBLEMS JUST REQUIRE SIMPLE ARITHMETIC
 No need to set up an equation.
o The unknown is already “by itself” and you are being given all the numbers
to calculate it!
 Imagine yourself in the problem:
o What would you naturally do in such a situation?
o Add? Subtract? Multiply? Divide?
o One step at a time!
 Cannot do it mechanically! You have to think and imagine what one would
naturally do in such a situation.
Plumber charges $50 to show up and $30/hour; what is the cost of a
5 hour job?
Flat rate + hourly cost x number of hours = cost of job
50 + 30(5) = 200

14. BASIC SET-UP SKILLS THATCAN BE
USED FOR WORD PROBLEMS
 Ratio and proportion (LOTS of these).
o Set up and solve a proportion
o Find the parts of a whole given a ratio
of parts and the total (MANY of
these).
 Conversions (LOTS of these)
o Unit cancellation
o Or by proportion if you prefer

15.  Percentage problems (LOTS of these)
o Given whole and percent, find the
part
o Given part and whole, find the
percent
o Given part and percent, find the
whole.
o Find percent increase or decrease.
 Rate problems:
o Distance = rate(time) (d = rt)
o Or r = d/t, or t = d/r
 But some word problems don’t easily fit
one of these categories.

16. Our Services
Study Help
• Drop-In Study Help for all courses
• Study Groups
• Question Drop-Off
Student Tech Help
• Live Chat
• Scheduled Lab Consultations
• Ask-a-Lab Associate Email
• Get Tech Ready and Appy Hour Workshops
Learning Help
• Check out our collection of self-service resources that supplement classroom materials
Get In Touch!
www.wccnet.edu/LC (live chat assistance offered during regular hours)
(734) 973-3420
Email: LCLab@wccnet.edu