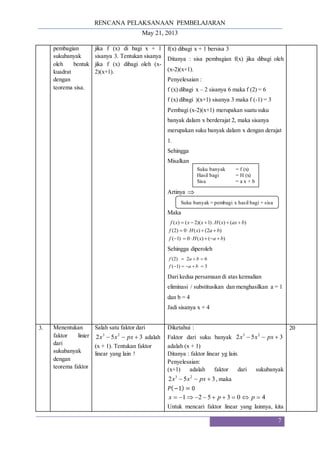
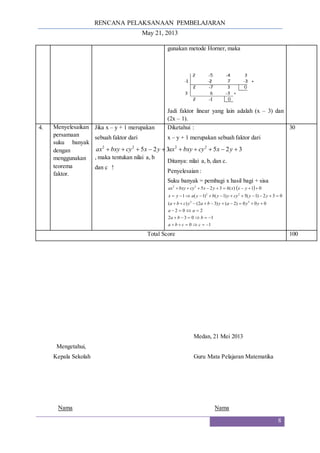
Dokumen ini adalah Rencana Pelaksanaan Pembelajaran (RPP) untuk mata pelajaran matematika di SMA, berfokus pada penggunaan teorema sisa dan teorema faktor dalam menyelesaikan masalah suku banyak. Tujuan pembelajaran mencakup kemampuan menentukan sisa pembagian dan faktor linier dari suku banyak. Metode pengajaran meliputi ceramah, diskusi, dan latihan soal, serta sumber referensi yang digunakan untuk mendukung materi ajar.

1. RENCANA
PELAKSANAAN
PEMBELAJARAN
SUKU BANYAK
Disusun oleh MARIA PRISCILLYA PASARIBU (4103312018)
Bilingual Pendidikan Matematika

2. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
1
RENCANA PELAKSANAAN PEMBELAJARAN (RPP)
NAMA SEKOLAH : SMA ....
MATA PELAJARAN : MATEMATIKA
KELAS / SEMESTER : XI IPA / 2 (GENAP)
ALOKASI WAKTU : 2x45’
A. Standar Kompetensi : 4. Menggunakan aturan sukubanyak dalam penyelesaian masalah.
B. Kompetensi Dasar: 4.2 Menggunakan teorema sisa dan teorema faktor dalam pemecahan
masalah.
C. Indikator : 1. Menentukan sisa pembagian sukubanyak oleh bentuk linier dan kuadrat
dengan teorema sisa.
2. Menentukan faktor linier dari sukubanyak dengan teorema faktor.
3. Menyelesaikan persamaan suku banyak dengan menggunakan teorema
faktor.
D. Tujuan Pembelajaran: 1. Peserta didik mampu menentukan sisa pembagian sukubanyak oleh
bentuk linier dan kuadrat dengan teorema sisa.
2. Peserta didik mampu menentukan faktor linier dari sukubanyak
dengan teorema faktor.
3. Peserta didik mampu menyelesaikan persamaan sukubanyak dengan
menggunakan teorema faktor.
E. Materi Ajar :
Teorema Sisa
Diketahui, 𝑃(𝑥) = 𝑎𝑛𝑥𝑛 + 𝑎𝑛−1𝑥𝑛−1 + ⋯+ 𝑎2𝑥2 + 𝑎1𝑥 + 𝑎0. Cara Anda menentukan sisa
pembagian dari pembagian suku banyak P(x) oleh bentuk (x – k),(ax + b),dan (ax2 + bx + c),
baik dengan cara Horner maupun dengan cara pembagian biasa telah dipelajari pada pelajaran
sebelumnya.
Sekarang amatilah persamaan berikut:
P(x) = f(x) . H(x) + S

3. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
2
P(x) : suku banyak yang dibagi
f(x) : pembagi
H(x) : hasil bagi
S : sisa pembagian
Jika P(x) berderajat n dan f(x) berderajat m (m ≤ n) maka derajat H(x) dan S masing-masing
sebagai berikut.
• derajat H(x) adalah (n – m)
• derajat maksimum S adalah (m – 1)
1. Pembagian dengan Pembagi (ax + b )
Jika f(x) = ax + b, merupakan pembagi dari P(x) maka hubungan antara P(x) dan f(x)
dapat ditulis sebagaiberikut.
𝑃(𝑥) = (𝑎𝑥 + 𝑏)(
𝐻(𝑥)
𝑎
) + 𝑆, berlaku untuk setiap x bilangan real.
Oleh karena f(x) berderajat satu maka S berderajat nol. Jadi, konstanta S sama dengan A0.
Sisa pembagian dapat ditentukan dengan menggunakan
teorema berikut.
Teorema 1.1
Jika suku banyak P(x) yang berderajat n dibagi dengan (ax + b) maka sisanya adalah
𝑃(−
𝑏
𝑎
).
Bukti :
harus ditunjukkan bahwa 𝑆 = 𝑃(−
𝑏
𝑎
), Jika suku banyak P(x) berderajat n dibagi dengan
(ax + b), bentuk pembagian itu dituliskan sebagai berikut
𝑃(𝑥) = (𝑎𝑥 + 𝑏)(
𝐻(𝑥)
𝑎
) + 𝑆 ... (1)
Selanjutnya, substitusikan nilai 𝑥 = −
𝑏
𝑎
ke persamaan (1) sehingga diperoleh
𝑃(−
𝑏
𝑎
) = (𝑎(−
𝑏
𝑎
) + 𝑏) (
𝐻 (−
𝑏
𝑎
)
𝑎
) + 𝑆
= (−𝑏 + 𝑏) (
𝐻(−
𝑏
𝑎
)
𝑎
) + 𝑆
𝑃(−
𝑏
𝑎
) = 𝑆.
Jadi, sisa = 𝑃 (−
𝑏
𝑎
).Teorema terbukti.
Contoh 1.
Carilah sisa pembagian dari (4x3
+ 2x2
– 4x + 6) : (x – 3) tanpa melakukan pembagian
terlebih dahulu.

4. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
3
Jawab:
Suku banyak P(x) = 4x3
+ 2x2
– 4x + 6 dibagi dengan (x – 3) sisanya adalah
𝑆 = 𝑃 (−
−3
1
) = 𝑃(3) berdasarkan teorema 1.1
Jadi, dengan menyubstitusikan x = 3 ke dalam fungsi P(x),diperoleh
P(3) = 4 . 33
+ 2 . 32
– 4 . 3 + 6 = 120.
Dengan demikian, sisa pembagiannya adalah 120.
2. Pembagian dengan Pembagi (x-a)(x-b)
Suatu suku banyak p(x) yang dibagi oleh f(x) = (x – a)(x – b),dapat dituliskan sebagai
berikut.
P(x) = (x – a) (x – b) H(x) + S … (1)
berlaku untuk setiap x bilangan real. f(x) = (x – a) (x – b) berderajat 2 sehingga sisanya
berderajat maksimum satu, atau 𝑆 = 𝐴0 + 𝐴1𝑥
Coba Anda jelaskan mengapa sisanya berderajat maksimum satu. Dengan demikian,
persamaan (1) dapat dituliskan sebagai berikut.
𝑃(𝑥) = (𝑥 – 𝑎)(𝑥 – 𝑏)𝐻(𝑥) + 𝐴0 + 𝐴1𝑥
Sisa dapat ditentukan dengan teorema sisa, yaitu sebagaiberikut.
 Untuk pembagi (x – a),diperoleh sisa
𝑃(𝑎) = 0. 𝐻(𝑎) + 𝐴0 + 𝐴1𝑎
= 𝐴0 + 𝐴1𝑎 ...(2)
 Untuk pembagi (x – b),diperoleh sisa
𝑃(𝑏) = 0.𝐻(𝑏) + 𝐴0 + 𝐴1𝑏
= 𝐴0 + 𝐴1𝑏 ....(3)
Dari persamaan (2) dan (3), kita dapat menemukan rumus
B. Teorema Faktor
1. Pengertian Teorema Faktor
Pandanglah suku banyak P(x) dan pembagi ax + b. Kemudian, amati kembali Teorema
1.1 dengan saksama. Jika sisanya 0, apa yang terjadi dengan (ax + b)? Sebagai akibat
dari Teorema 1.1, jika sisa 𝑃 (−
𝑏
𝑎
) = 0, maka
𝑃(𝑥) = (𝑎𝑥 + 𝑏)(
𝐻(𝑥)
𝑎
) + 0
⇔ 𝑃(𝑥) = (𝑎𝑥 + 𝑏) (
𝐻(𝑥)
𝑎
) dengan 𝑎 ≠ 0.

5. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
4
Hal ini menunjukkan bahwa (ax + b) adalah suatu faktor dari P(x). Dengan demikian,
dapat dikatakan jika P(x) adalah suatu polinom, ax + b adalah pembagi, dan sisa
pembagiannya adalah 0 atau 𝑃 (−
𝑏
𝑎
) = 0, maka ax + b adalah faktor dariP(x).
Teorema 1.2
Jika 𝑃(𝑥) = 𝑎𝑛𝑥𝑛 + 𝑎𝑛−1𝑥𝑛−1 + ⋯+ 𝑎2𝑥2 + 𝑎1𝑥 + 𝑎0 dengan 𝑎𝑖 bilangan bulat, i = 1,
2, ...,n dan p bilangan bulat dengan p merupakan harga nol dari P(x) maka p adalah
pembagi 𝑎0.
Bukti :
Misal, p bilangan bulat yang merupakan harga nol P(x) maka
𝑃(𝑝) = 𝑎𝑛𝑝𝑛 + 𝑎𝑛−1𝑝𝑛−1 + ⋯+ 𝑎2𝑝2 + 𝑎1𝑝 + 𝑎0 = 0
𝑎𝑛𝑝𝑛 + 𝑎𝑛−1𝑝𝑛−1 + ⋯+ 𝑎2𝑝2 + 𝑎1𝑝 = −𝑎0
𝑝(𝑎𝑛𝑝𝑛−1 + 𝑎𝑛−1𝑝𝑛−2 + ⋯+ 𝑎1) = −𝑎0
Oleh karena p adalah bilangan bulat dan 𝑎𝑖 juga adalah bilangan bulat maka ruas kiri
persamaan tersebut merupakan bilangan bulat.
Jadi, p pembagi dari 𝑎0 (terbukti).
2. Penggunaan Teorema Faktor untuk Mencari Akar Persamaan Suku Banyak
Diketahui, P(x) suku banyak dengan bentuk:
𝑃(𝑥) = 𝑎𝑛𝑥𝑛 + 𝑎𝑛−1𝑥𝑛−1 + ⋯+ 𝑎2𝑥2 + 𝑎1𝑥 + 𝑎0
(x – k) adalah faktor linear P(x) jika dan hanya jika k akar persamaan P(x) = 0. Jika suku
banyak P(x) berderajat n maka persamaan P(x) = 0 maksimum mempunyai n buah akar.
F. Model dan Metode Pembelajaran
A. Model Pembelajaran : Model Pengajaran Langsung (MPL)
B. Metode Pembelajaran : ceramah,diskusi, tanya jawab
G. Skenario Pembelajaran
Aktivitas Waktu Kegiatan Pembelajaran
Guru Peserta didik
Pendahuluan 10’  Motivasi : Jika anda sukses
berbagilah kepada yang lain, jika
anda gagal tanyakanlah pada diri
anda mengapa anda gagal
 Mengingatkan kembali tentang
 Mendengar dan menelaah
motivasi yang diberikan
 Mengingat kembali
tentang bentuk umum,
nilai, dan pembagian

6. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
5
bentuk umum, nilai, dan
pembagian suku banyak.
suku banyak.
Kegiatan
Inti
70’  Guru menjelaskan dasar-dasar
dari teorema sisa dan memberikan
kesempatan kepada peserta didik
untuk bertanya.
 Guru menjelaskan bagaimana
pembagian suku banyak dengan
pembagi (ax+b) dan memberikan
kesempatan kepada peserta didik
untuk bertanya
 Guru menjelaskan bagaimana
pembagian suku banyak dengan
pembagi (x-a)(x-b) dan
memberikan kesempatan kepada
peserta didik untuk bertanya
 Guru menjelaskan dasar-dasar
dari teorema faktor dan
memberikan kesempatan kepada
peserta didik untuk bertanya.
 Guru menjelaskan bagaimana
menggunakan Teorema Faktor
untuk mencari akar persamaan
suku banyak.
 Guru memberikan latihan soal
untuk diselesaikan bersama-sama
dengan peserta didik
 Peserta didik
mendengarkan penjelasan
tentang dasar-dasar dari
teorema sisa dan
mengajukan pertanyaan.
 Peserta didik
mendengarkan penjelasan
bagaimana pembagian
suku banyak dengan
pembagi (ax+b) dan
mengajukan pertanyaan
 Peserta didik
mendengarkan penjelasan
bagaimana pembagian
suku banyak dengan
pembagi (x-a)(x-b) dan
mengajukan pertanyaan
 Peserta didik
mendengarkan penjelasan
tentang dasar-dasar dari
teorema faktor dan
mengajukan pertanyaan.
 Peserta didik
mendengarkan penjelasan
bagaimana menggunakan
Teorema Faktor untuk
mencari akar persamaan
suku banyak.
 Peserta didik membahas
latihan soal yang
diberikan oleh guru dan
diarahkan oleh guru.
Penutup 10’  Guru memberikan kesempatan  Peserta didik

7. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
6
kepada peserta didik untuk
membuat kesimpulan dari materi
yang diajarkan.
 Guru menyimpulkan materi yang
diajarkan.
 Guru memberikan PR mengenai
teorema sisa dan teorema faktor.
menyimpulkan materi
yang telah diajarkan oleh
guru.
 Peserta didik menyimak
dan mencatat kesimpulan
yang diberikan oleh guru.
 Peserta didik mencatat
PR yang diberikan oleh
guru.
I. Sumber / Sarana / Alat
Sumber :
a. Buku Seribu pena Matematika SMA Kelas XI jilid 2, karangan Drs. Husein Tamponas
(penerbit: Erlangga).
b. Buku Matematika SMA Kelas XI Semester 2, karangan Sartono Wirodikromo (penerbit:
Erlangga).
J. Penilaian
Teknik : tugas individu
Bentuk Instrumen : uraian singkat
Contoh Instrumen : Lembar Kerja Siswa
No. Indikator Soal Penyelesaian Penilaian
1. Menentukan
sisa
pembagian
sukubanyak
oleh bentuk
linier dengan
teorema sisa.
Tentukan sisa pembagian
x
x
x
x
x
f 2
1
2
3
4
4
)
( 



dibagi oleh  
2
2 
x !
Diketahui :
Suku banyak : x
x
x
x
x
f 2
1
2
3
4
4
)
( 



Pembagi :  
2
2 
x
Ditanya : sisa pembagian.
Penyelesaian :
𝑆 = 𝑓 (−
𝑏
𝑎
) = 𝑓 (−
√2
2
)
Maka, sisa pembagian dari suku banyak itu
adalah
2
1
2
2
.
4
)
2
(
)
2
(
)
2
(
)
2
(
4
)
2
(
4
1
2
1
4
1
4
1
2
1
2
1
2
2
1
3
2
1
4
2
1
2
1














f
20
2. Menentukan
sisa
Suatu suku banyak f (x) di
bagi x – 2 sisanya 6 dan
Diketahui :
f(x) dibagi x – 2 bersisa 6
30

8. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
7
pembagian
sukubanyak
oleh bentuk
kuadrat
dengan
teorema sisa.
jika f (x) di bagi x + 1
sisanya 3. Tentukan sisanya
jika f (x) dibagi oleh (x-
2)(x+1).
f(x) dibagi x + 1 bersisa 3
Ditanya : sisa pembagian f(x) jika dibagi oleh
(x-2)(x+1).
Penyelesaian :
f (x) dibagi x – 2 sisanya 6 maka f (2) = 6
f (x) dibagi )(x+1) sisanya 3 maka f (-1) = 3
Pembagi (x-2)(x+1) merupakan suatu suku
banyak dalam x berderajat 2, maka sisanya
merupakan suku banyak dalam x dengan derajat
1.
Sehingga
Misalkan
Artinya 
Maka
)
(
)
(
0
)
1
(
)
2
(
)
(
0
)
2
(
)
(
)
(
.
)
1
)(
2
(
)
(
b
a
x
H
f
b
a
x
H
f
b
ax
x
H
x
x
x
f















Sehingga diperoleh
3
)
1
(
6
2
)
2
(








b
a
f
b
a
f
Dari kedua persamaan di atas kemudian
eliminasi / substitusikan dan menghasilkan a = 1
dan b = 4
Jadi sisanya x + 4
3. Menentukan
faktor linier
dari
sukubanyak
dengan
teorema faktor
Salah satu faktor dari
3
5
2 2
3


 px
x
x adalah
(x + 1). Tentukan faktor
linear yang lain !
Diketahui :
Faktor dari suku banyak 3
5
2 2
3


 px
x
x
adalah (x + 1)
Ditanya : faktor linear yg lain.
Penyelesaian:
(x+1) adalah faktor dari sukubanyak
3
5
2 2
3


 px
x
x , maka
𝑃(−1) = 0
4
0
3
5
2
1 








 p
p
x
Untuk mencari faktor linear yang lainnya, kita
20
Suku banyak = f (x)
Hasil bagi = H (x)
Sisa = a x + b
Suku banyak = pembagi x hasil bagi + sisa

9. RENCANA PELAKSANAAN PEMBELAJARAN
May 21, 2013
8
gunakan metode Horner, maka
Jadi faktor linear yang lain adalah (x – 3) dan
(2x – 1).
4. Menyelesaikan
persamaan
suku banyak
dengan
menggunakan
teorema
faktor.
Jika x – y + 1 merupakan
sebuah faktor dari
3
2
5
2
2




 y
x
cy
bxy
ax
, maka tentukan nilai a, b
dan c !
Diketahui :
x – y + 1 merupakan sebuah faktor dari
3
2
5
2
2




 y
x
cy
bxy
ax
Ditanya: nilai a, b, dan c.
Penyelesaian :
Suku banyak = pembagi x hasil bagi + sisa
 
1
0
1
0
3
2
2
0
2
0
0
0
)
2
(
)
3
2
(
)
(
0
3
2
)
1
(
5
)
1
(
)
1
(
1
0
1
)
(
3
2
5
2
2
2
2
2
2















































c
c
b
a
b
b
a
a
a
y
y
a
y
b
a
y
c
b
a
y
y
cy
y
y
b
y
a
y
x
y
x
x
h
y
x
cy
bxy
ax
30
Total Score 100
Medan, 21 Mei 2013
Mengetahui,
Kepala Sekolah Guru Mata Pelajaran Matematika
Nama Nama