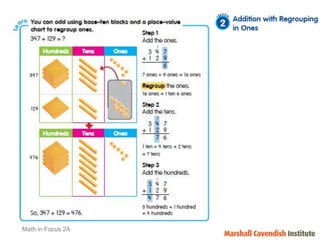
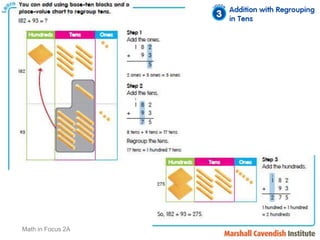
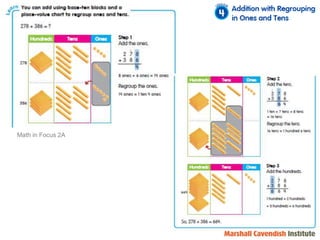
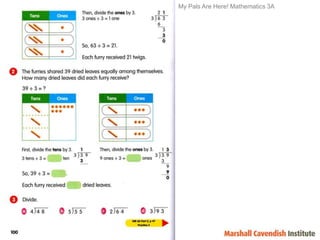
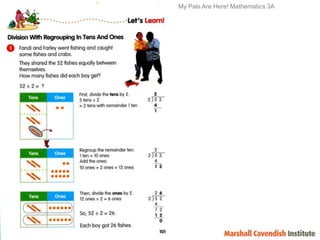
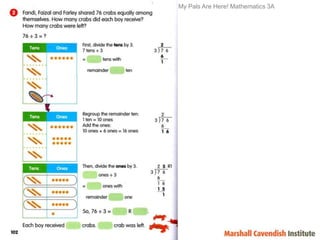
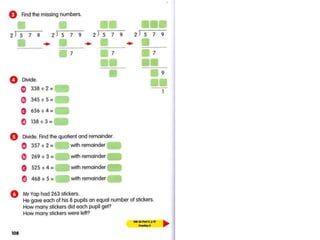
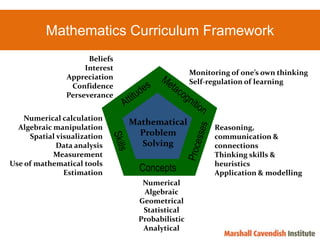
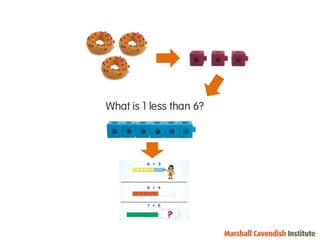
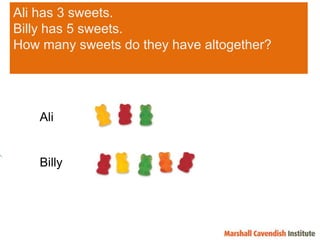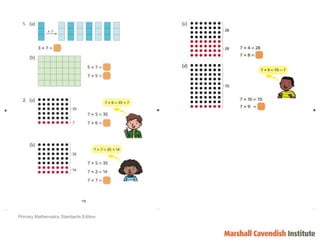
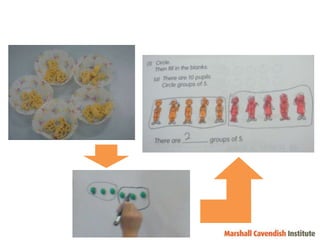
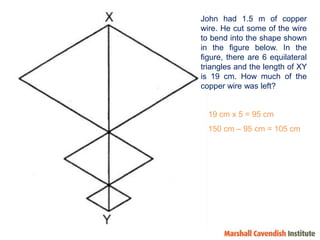
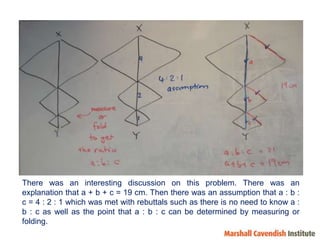
1) The document discusses features of the Singapore Math method, including its focus on visualization and the model method. 2) It provides examples of how the bar model method can be used to represent word problems involving part-whole, comparison, and before-after situations. 3) The discussion emphasizes using student responses to modify problems and make the lesson more challenging in order to focus on conceptual understanding.

1. Singapore Math in Rotterdam 2Opleiding Singapore rekenspecialistReview of Day 1What are some features of Singapore Math and its theoretical underpinnings.On Day 2, we look at the focus on visualization and the model method.

2. Review of Day 1Yeap Ban Har, Ph.D.Marshall Cavendish InstituteSingaporebanhar@sg.marshallcavendish.com

3. VariationsTasks are varied in a systematic way to ensure that average and struggling learners can learn well.

4. Math in Focus 2A

5. Math in Focus 2A

6. Math in Focus 2A

7. ZoltanDienesThe three lessons include mathematical variations within the same grade. This is referred to as a spiral approach.

8. It is likely that a teacher will start this unit using the sticks. This is followed by the use of base ten blocks. Finally, non-proportionate materials such as coins are used. In each of these lessons, the teacher is likely to introduce the following five notations in turn – place value chart, expanded notation, number in numerals, number in words and the tens and ones notation.The question is what is an appropriate sequence? Should the place value chart be used first? Or the expanded notation? Give your reasons.Place Value ChartExpanded NotationWordsNumeralsTens and Ones NotationPrimary Mathematics

9. ZoltanDienesThis lesson include perceptual variations. This is Dienes’ idea of multiple embodiment. The mathematical concept is constant while the materials used to embody it are varied.

10. Jerome BrunerBruner advised teachers to use the CPA Approach in teaching mathematics.

12. Richard SkempSkemp distinguished between instrumental understanding from relational understanding to encourage teachers to teach for conceptual understanding.

13. skemp’stheoryconceptualunderstandingBinaBangsa School, Semarang, Indonesia

14. Example 2Division in Other Grade Levels

15. My Pals Are Here! Mathematics 3A

16. My Pals Are Here! Mathematics 3A

17. My Pals Are Here! Mathematics 3A

18. My Pals Are Here! Mathematics 3A

19. My Pals Are Here! Mathematics 3A

20. My Pals Are Here! Mathematics 3A

21. My Pals Are Here! Mathematics 3A

22. My Pals Are Here! Mathematics 3A

23. My Pals Are Here! Mathematics 3A

25. Keys Grade School, Manila, The Philippines

26. Keys Grade School, Manila, The Philippines

27. The Bar Model Methodde strookmodelYeap Ban Har, Ph.D.Marshall Cavendish InstituteSingaporebanhar@sg.marshallcavendish.com

28. BeliefsInterestAppreciationConfidencePerseveranceMonitoring of one’s own thinkingSelf-regulation of learningAttitudesMetacognitionNumerical calculationAlgebraic manipulationSpatial visualizationData analysisMeasurementUse of mathematical toolsEstimationMathematical Problem SolvingReasoning, communication & connectionsThinking skills & heuristicsApplication & modellingSkillsProcessesConceptsNumericalAlgebraicGeometricalStatisticalProbabilisticAnalyticalMathematics Curriculum Framework

29. visualizationWellington Primary School

30. Primary Mathematics Standards Edition

32. John had 1.5 m of copper wire. He cut some of the wire to bend into the shape shown in the figure below. In the figure, there are 6 equilateral triangles and the length of XY is 19 cm. How much of the copper wire was left? 19 cm x 5 = 95 cm150 cm – 95 cm = 105 cm

33. There was an interesting discussion on this problem. There was an explanation that a + b + c = 19 cm. Then there was an assumption that a : b : c = 4 : 2 : 1 which was met with rebuttals such as there is no need to know a : b : c as well as the point that a : b : c can be determined by measuring or folding.

34. The Bar Model Methodde strookmodelYeap Ban Har, Ph.D.Marshall Cavendish InstituteSingaporebanhar@sg.marshallcavendish.com

35. Ali has 3 sweets. Billy has 5 sweets.How many sweets do they have altogether?AliBilly

36. Ali has 3 sweets. Billy has 5 sweets.How many sweets do they have altogether?AliBilly

38. IntroductionThe focus is on the bar model method.

39. Materials developed by Poon Yain Ping

40. Materials developed by Poon Yain Ping

41. Materials developed by Poon Yain Ping

42. SummaryThe three basic situations are part-whole, comparison and before-after situations.

43. Materials developed by Poon Yain Ping

44. The class decided that this was impossible. The teacher asked the class to change this to another number to make the situation possible. We discussed when it is 3, 4 and 5 times.A student gave an incorrect solution for the second part. The teacher asked students to write a question for which this would be a correct solution.Materials developed by Poon Yain Ping

45. SummaryWe discussed how to use students’ responses to make the lesson focus on depth. We also saw how a problem can be modified to challenge learners.

46. Materials developed by Poon Yain Ping

47. Materials developed by Poon Yain Ping

48. Materials developed by Poon Yain Ping

49. School Assessmentwomenmen

50. School Assessmentwomen45men12

51. School Assessmentwomenmen?women4566men12

52. Further Practice for Model Method

53. Materials developed by Poon Yain Ping

54. Materials developed by Poon Yain Ping

55. Materials developed by Poon Yain Ping

56. Materials developed by Poon Yain Ping

57. Materials developed by Poon Yain Ping

58. Materials developed by Poon Yain Ping

59. Materials developed by Poon Yain Ping

60. Materials developed by Poon Yain Ping

61. Materials developed by Poon Yain Ping

62. Materials developed by Poon Yain Ping

63. Materials developed by Poon Yain Ping