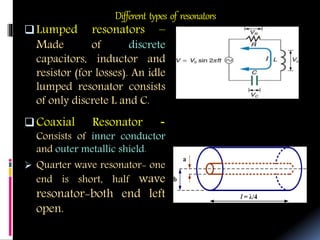
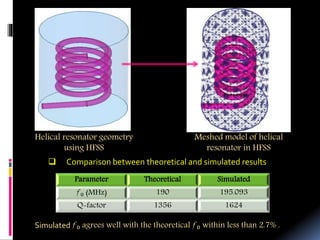
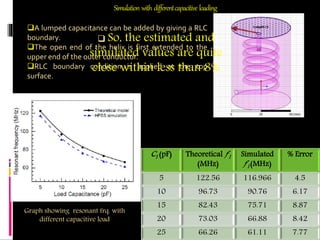
The document outlines the design of a helical resonator for use in a penning ion trap. It discusses different types of resonators and why a helical design is best. The document provides details on the design parameters and theoretical calculations for a 190 MHz helical resonator. Simulations of the resonator were performed using HFSS software, finding good agreement with theoretical resonant frequency and Q-factor values. The effect of different capacitive loads on resonant frequency was also studied through simulations. In conclusion, the helical resonator design is suitable for detection of charged particles in the penning ion trap application.

2. Outline
 A brief idea about penning ion trap
 Different types of resonator
 Comparison between the resonators
 Details of Helical resonator
 Simulation of Helical resonator (in HFSS)
 Comparison between the estimated and simulated
results
 Conclusion

3. A brief idea about penning ion trap
 Apparatus for confinement of charged particle.
 Incorporates both magnetic and electrostatic field
 A strong homogeneous magnetic field is applied
along Z direction
 A weak, static, quadropolar electric field is applied
 Quadropolar electric field is achieved by using a
hyperboloid trap electrode.

4. The different motions of trappedparticles
 Due to the strong, homogeneous magnetic field particle
shows a two dimensional harmonic motion, called
Cyclotron motion. Thus achieved radial confinement.
 But in axial direction there is no effect of magnetic field,
axial confinement is obtained only due to applied
quadropolar electrostatic field.
 Superposition of the magnetic field and electric field
results in three independent motion of trapped ions.
Axial motion (ωZ)
Reduced cyclotron motion
(ω+)
Magnetron motion (ω-)
ω+ > ωZ > ω-

5. Signal detection in penning trap
AmplifierAmplifier
 The moving trapped ions
have an effect of induced
current on the trap electrode
 The perpendicular motion of
the ions cause a temporal
change of image charges
induced on the plate.
 Image current is thus
produced.
 This current is very weak
(~100fA)
 The induced image current
offers a voltage drop on the
RLC circuit.
 Maximum voltage is obtained
when
resonant frequency of LCR
circuit = Axial frequency of ion
MHzC
md
qU
f dc
Z 64
2
1
22


This voltage is amplified by a high impedance low noise
amplifier.

6. Main Objective
 As the signal is very weak a high Q resonator is
required.
 It is found that the resonant circuit should have a
resonant frequency in the range of (60-70) MHz in
the loaded condition.
 Also the size of the resonator is a matter to be
considered. A compact resonator is required as space
is a constraint.
 In order to satisfy these conditions we have to first
study what kind of resonator is appropriate in this
experimental set up.

7. Different types of resonators
Lumped resonators –
Made of discrete
capacitors, inductor and
resistor (for losses). An idle
lumped resonator consists
of only discrete L and C.
Coaxial Resonator -
Consists of inner conductor
and outer metallic shield.
 Quarter wave resonator- one
end is short, half wave
resonator-both end left
open.

8. Continued..
 Helical Resonator – Special kind of coaxial
resonator, inside the outer cylindrical shield there
is a helical coil.
 One end of the helix is connected to the outer
shield.
 Other end is left open.
 Acts as a quarter wave resonator.
Outer
shield
Helical
coil

9. Comparison between the resonators
 In lumped resonators, high Q value can be obtained by using a large
lumped inductor, it makes system bulky and unfeasible for use.
 Provide a maximum Q ≈ 200
 In coaxial resonator, high Q- factor can be achieved but these are
very bulky in size.
 Provides a Q-factor ~ very high
 With helical resonator a reasonably high Q value can be obtained, as
well as it has a compact size.
 Provides Q –factor ~ several thousands
 Hence it is clear that helical resonator is the best choice among these three.
Lumped
resonator
Coaxial
resonator
Helical
resonator
Q factor Low Very high High
Size Portable Bulky Portable
Design Easy Easy Complex

10. Design parametersofHelical resonator
For a given shield diameter (D)
and resonant frequency (ƒ₀)
D = inside diameter of shield
d = mean diameter of the of turns
B = inside length of the shield
b = axial length of coil
do= diameter of conductor.
τ = pitch of winding
Qu=Unloaded resonant freq.
Units- Lengths are in inches and
frequency in MHz
•Design guidelines provided by Macalpine et al.[7]

11. Effective capacitance of the helical resonator
 The helical resonator has an effective self capacitance (Ce) and capacitance
contributed from the ion trap and LNA which is roughly estimated to be the order
of (15-20) pF.
 The resonator should resonate at the freq range of (60-70)MHz after a capacitive
loading of (15-20) pF. (Cl )
 In order to calculate the resonant frequency under different capacitive loading,
the self capacitance of the resonator should be estimated first.
𝐶𝑐 = helical coil self-capacitance and 𝐶𝑠 = helical coil to the surrounding shield capacitance,
by empirical formula [using ref. 8]
10
10
27.0
08.01126.0.1 











 d
d
bd
b
CC
12
10
log
75.0
37.39.2 








d
D
bC S
  cCO CNC 1.3 
1
.4


N
C
C S
SO
SOCO CCC 1.5
1,
11
1
.6
1




NC
CC
CC SO
CON
Ne
0f
CC
C
f
le
e
l



12.  Resonant frequency of the helical resonator with different capacitive
load
 Observation
 From above table, though design frequency 180MHz gives loaded resonant
frequency, within the required range
60 < 66.243 < 70 MHz
 But, we are going to choose design frequency of 190 MHz, as the value of
unloaded resonant frequency will be 2-5% lower in the actual fabricated
resonator. (due to teflon core).
f0 (MHz) Ce (pF) Cl (pF) fl (MHz)
160 3.028 20 58.02
170 3.028 20 61.65
180 3.133 20 66.243
190 3.26 20 71.13

13. Design parameters of 190 MHz helical resonator
 Theoretically calculated Q factor - 1356
Parameters Values
Shield inner dia. (D) 50 mm
Core mean dia. (d) 27.5 mm
Axial length of coil (b) 41.25 mm
Shield inside length (B) 66.25 mm
Turns No. (N) 5
Axial pitch (τ) 8.12 mm/turn
Conductor dia. (d0) 4.06mm

14. Simulation
 High Frequency Structure Simulation (HFSS)
 industry standard tool for 3-d full wave electromagnetic field
simulation.
 Involves finite element method (FEM) for solving electromagnetic
field inside the structure.
 The geometric model is automatically divided into large number of
tetrahedral.
 The finite elements used by HFSS are tetrahedra, and the entire
collection of tetrahedra is called a mesh.
 A solution is found for the field within the finite elements.
 Uses the above process repeatedly, for higher accuracy, called
iterative solution process .

15. Helical resonator geometry
using HFSS
Meshed model of helical
resonator in HFSS
Parameter Theoretical Simulated
ƒ₀ (MHz) 190 195.093
Q-factor 1356 1624
 Comparison between theoretical and simulated results
Simulated ƒ₀ agrees well with the theoretical ƒ₀ within less than 2.7% .

16. Simulation with differentcapacitive loading
A lumped capacitance can be added by giving a RLC
boundary.
The open end of the helix is first extended to the
upper end of the outer conductor.
RLC boundary condition is applied at the top
surface.
Graph showing resonant frq. with
different capacitive load
Cl (pF) Theoretical ƒl
(MHz)
Simulated
ƒl (MHz)
% Error
5 122.56 116.966 4.5
10 96.73 90.76 6.17
15 82.43 75.71 8.87
20 73.03 66.88 8.42
25 66.26 61.11 7.77
 So, the estimated and
simulated values are quite
close within less than 8%

17. Conclusion
 Quarter wave helical resonator has been designed for
detection of charged particles in the penning ion trap.
 Theoretical and simulated values are compared and
agreed well.
 Effect of different capacitive loading has been studied.
 Simulation is done by using ANSYS HFSS software.
 In future, the resonator will be fabricated and tested
with different capacitive load , and after comparing
with the simulated results it will be used in
experimental set up for penning ion trap.

18. References
 [1] K. Blaum, “High-accuracy mass spectrometry with stored ions,” Physics Report, Vol.
425, pp. 1-78, January 2006
 [2] W. Shockley, Journal of Applied Physics, 9, 635 (1938)
 [3] David M. Pozar, “Microwave Engineering”, 3nd Ed., Ch.6, Wiley, 2009.
 [4] Saikat Sarkar, Ph.D Thesis: "Design and development of a compact helical
resonator for charged particle detection application" Submitted to The University of
Burdwan (2015)
 [5] Peter Vizmuller, "RF Design Guide", Artech house,2nd Ed., pp. 237-240, 1995.
 [6] V.S. Bagal, "Microwave Engineering", Technical publication Pune,1st Ed., pp. 2-19,
2009
 [7] W.W.Macalpine and R.O.Schildknecht,”Coaxial resonator with helical inner
conductor,” Proc.IRE 47,2099(1959).
 [8] K.Deng, Y.L.Sun, W.H.Yuan, Z.T.Xu, J.Zhang, Z.H.Lu and J.Luo,” A Modified model
of helical resonator with predictable loaded resonant Frequency and Q-factor,"
Rev.Sci.Instrum.85, 104706(2014).
 [9] HFSS v10 User Guide - Anlage Research Group http://www
anlage.umd.edu/HFSSv10UserGuide.pdf
 [10] RF & Microwave - ANSYS http://www
www.ansys.com/Products/Simulation+Technology/.../RF+&+Microwave

19. Acknowledgement
 I wish to express my gratitude to Dr. P.Y. Nabhiraj for providing
me opportunity to carry out my project work at VECC.
 I sincerely thank my project guide Mrs. Parnika Das for her
guidance.
 I am grateful to Mr. Ashif reza for his wonderful cooperation
and technical discussions. I Also thank Shri. Anurag Mishra for
his suggestions.
 A special thanks goes to all other members of VECC.
 Most of all, I would like to thank all of my teachers.
 And last but not the least I owe my sincere thanks to my family
and mates for their encouragement.