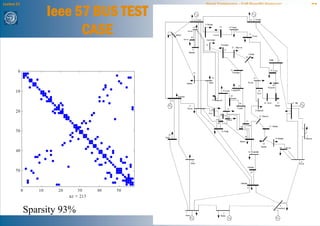
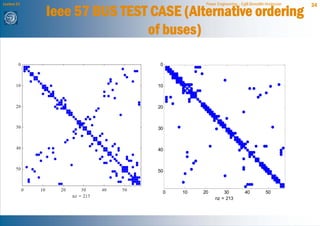
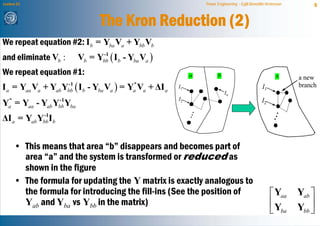
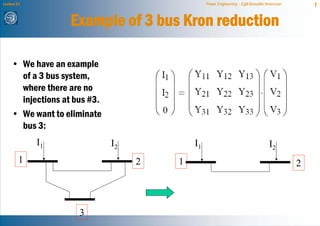
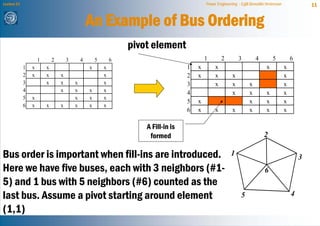
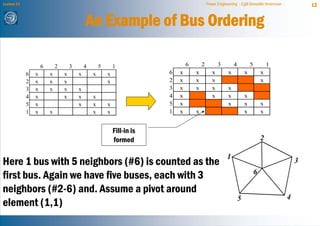
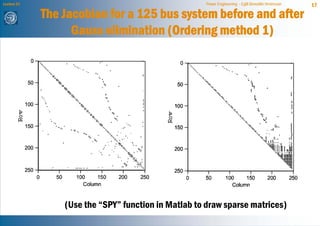
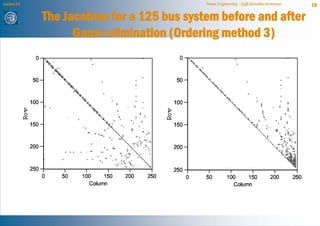
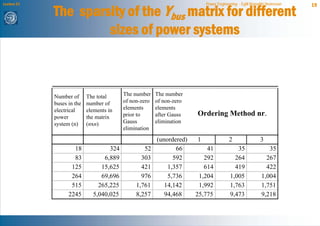
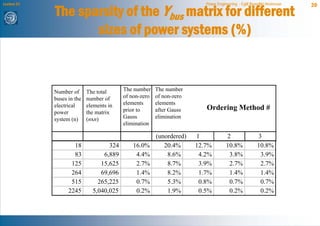
The document discusses network reduction techniques for solving power flow calculations more efficiently. It introduces the concept of "fill-ins" that occur during Gaussian elimination, which are analogous to introducing new branches when eliminating nodes during network reduction. The Kron reduction method is described, which eliminates nodes by integrating them into other areas of the network. This introduces corrections for injections and admittances in the reduced system, similar to fill-ins. An example of reducing a 3 bus system is provided. Different node ordering methods for Gaussian elimination are presented to minimize introduced fill-ins when solving large power networks.

1. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 1
Sparse Matrices in Power Flow
Calculations (2)

2. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 2
Network reduction and fill-ins
Introduction of “Fill-ins” in the Gauss elimination
process represents new branches in the network.
So, by eliminating nodes in the
network we may create new
branches

3. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 3
Fill ins and Network reduction
• The introduction of fill-ins is equivalent to
reducing the network by integrating a given
subset of buses with the rest of the system a b
(this is sometimes called “Kron reduction”)
• Assume a power system or a I1
general network consisting of 2 I2
In
areas (indexed “a” and “b”)
• Area “a” could be a whole country and area
“b” could be the rest of the continent. Note
that there can be tie-lines crossing the border
between areas
• We want to “integrate” all buses in area “b” ⎡Ia ⎤
into the area “a” or reduce the system I=⎢ ⎥
• I is a vector of partitioned injection currents ⎣ Ib ⎦
(generators/loads)
• V is a vector of partitioned bus voltages ⎡ Va ⎤
V=⎢ ⎥
⎣ Vb ⎦

4. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 4
The Kron Reduction
• We eliminate all nodes in area b
• This may create instead new
branches in area “a”
• We have a linear system often written as: Ax=b a b
⇔ In this case it can also be written: YV=I I1
• The system matrix and vectors In
are partitioned:
I2
⎡ Yaa Yab ⎤ ⎡ Va ⎤ ⎡ I a ⎤
⎢Y ⎥ ⎢ V ⎥ = ⎢I ⎥ We solve this by eliminating Vb from the 2nd
⎣ ba Ybb ⎦ ⎣ b ⎦ ⎣ b ⎦ equation and substitute it into the 1st
Yaa Va + Yab Vb = I a equation. We pivot around Ybb by eliminating
Yba Va + Ybb Vb = I b row and column “b”

5. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 5
The Kron Reduction (2)
We repeat equation #2: Ib = Yba Va + Ybb Vb
and eliminate Vb : Vb = Ybb ( Ib - Yba Va )
-1
We repeat equation #1: a b a a new
I a = Yaa Va + Yab Ybb ( Ib - Yba Va ) = Ya* Va + ΔI a
-1
I1 I1 branch
In
Ya* = Yaa - Yab Ybb Yba
-1 I2 I2
-1
ΔI a = Yab Ybb Ib
• This means that area “b” disappears and becomes part of
area “a” and the system is transformed or reduced as
shown in the figure
• The formula for updating the Y matrix is exactly analogous to
the formula for introducing the fill-ins (See the position of ⎡ Yaa Yab ⎤
Yab and Yba vs Ybb in the matrix) ⎢Y Ybb ⎥
⎣ ba ⎦

6. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 6
The Kron Reduction (2)
I = I a − ΔI a = Y Va
*
a
*
aa
ΔI a = Yab Y I -1
bb ab
Y = Yaa - ΔYaa
*
aa
ΔYaa = Yab Y Yba -1
bb
*
or I = Y Va
*
a aa
*
I = Y Va
*
a aa
• We see that ΔIa represents the corrections for
injections when reducing the system
• Similarly ΔYaa represents the correction for
admittances when reducing the system

7. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 7
Example of 3 bus Kron reduction
• We have an example
of a 3 bus system,
where there are no
injections at bus #3.
• We want to eliminate
bus 3:
I1 I2 I1 I2
1 2 1 2
3

8. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 8
Example of 3 bus Kron reduction
• We eliminate the I1 I2
voltage, V3 from the 1 2
last equation….
• …and substitute it
into the other
equations.
• =>We have reduced
the system and bus
#3 has disappeared

9. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 9
Network reduction
• The previous network reduction is named
after Gabriel Kron
• By eliminating part of the system and
integrating it in the rest, we may introduce
new links (updated Y) and new injections
(updated I)
• This is analogous to the fill-ins in the
Gauss elimination process

10. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 10
“Fill-in”s by Gauss Elimination
“Pivot” Column # p Column # j
aip ⋅ a pj
a = aij −
'
ij Line # p app apj
a pp
We pivot around the
element app . If both apj
and aip
are ≠ 0 it follows that aij Line # i aip aij
≠ 0, i.e. a fill-in is
formed where there was
zero previously.

11. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 11
An Example of Bus Ordering
pivot element
1 2 3 4 5 6 1 2 3 4 5 6
1 x x x x 1 x x x x
2 x x x x 2 x x x x
3 x x x x 3 x x x x
4 x x x x 4 x x x x
5 x x x x
5 x x x x
6 x x x x x x
6 x x x x x x
A Fill-in is
formed 2
Bus order is important when fill-ins are introduced. 1
3
Here we have five buses, each with 3 neighbors (#1- 6
5) and 1 bus with 5 neighbors (#6) counted as the
last bus. Assume a pivot starting around element 5 4
(1,1)

12. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 12
An Example of Bus Ordering
6 2 3 4 5 1 6 2 3 4 5 1
6 x x x x x x 6 x x x x x x
2 x x x x 2 x x x x
3 x x x x 3 x x x x
4 x x x x 4 x x x x
5 x x x x 5 x x x x
1 x x x x 1 x x x x
Fill-in is
formed 2
1
Here 1 bus with 5 neighbors (#6) is counted as the 3
first bus. Again we have five buses, each with 3 6
neighbors (#2-6) and. Assume a pivot around
5 4
element (1,1)

13. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 13
Optimal Ordering Method # 1
Order the nodes by starting with the node
which is initially connected to the
fewest other nodes. Ties can be
broken arbitrarily. (Parallel or shunt
connections can be skipped)
(This ordering rule is the simplest and has a
great benefit as compared to no ordering)

14. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 14
Optimal Ordering Method # 2
• Order the nodes in each step by selecting as the next node
the one with the fewest connections to
neighboring nodes (Including the effect of fill-
ins). Ties can be broken arbitrarily
• (This ordering rule is probably the best when weighing the
advantages and disadvantages)

15. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 15
Optimal Ordering Method # 3
• Order the nodes by selecting as the next node the node
which creates the fewest new branches. Ties can be
broken arbitrarily
• (The increased calculation speed according to this rules will
not outweigh the need for more memory and since all new
nodes have to be considered in each step)

16. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 16
Practical results how different
ordering methods introduce fill-ins
during the Gauss elimination process

17. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 17
The Jacobian for a 125 bus system before and after
Gauss elimination (Ordering method 1)
(Use the “SPY” function in Matlab to draw sparse matrices)

18. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 18
The Jacobian for a 125 bus system before and after
Gauss elimination (Ordering method 3)

19. The sparsity of the Ybus matrix for different
Lecture 21 Power Engineering - Egill Benedikt Hreinsson 19
sizes of power systems
Number of The total The number The number
buses in the number of of non-zero of non-zero
electrical elements in elements elements
power the matrix prior to after Gauss Ordering Method nr.
system (n) (nxn) Gauss elimination
elimination
(unordered) 1 2 3
18 324 52 66 41 35 35
83 6,889 303 592 292 264 267
125 15,625 421 1,357 614 419 422
264 69,696 976 5,736 1,204 1,005 1,004
515 265,225 1,761 14,142 1,992 1,763 1,751
2245 5,040,025 8,257 94,468 25,775 9,473 9,218

20. The sparsity of the Ybus matrix for different
Lecture 21 Power Engineering - Egill Benedikt Hreinsson 20
sizes of power systems (%)
Number of The total The number The number
buses in the number of of non-zero of non-zero
elements elements
electrical elements in
prior to after Gauss Ordering Method #
power the matrix
system (n) (nxn) Gauss elimination
elimination
(unordered) 1 2 3
18 324 16.0% 20.4% 12.7% 10.8% 10.8%
83 6,889 4.4% 8.6% 4.2% 3.8% 3.9%
125 15,625 2.7% 8.7% 3.9% 2.7% 2.7%
264 69,696 1.4% 8.2% 1.7% 1.4% 1.4%
515 265,225 0.7% 5.3% 0.8% 0.7% 0.7%
2245 5,040,025 0.2% 1.9% 0.5% 0.2% 0.2%

21. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 21
Other methods of solving linear
equations
Crout’s Method of LU Decomposition

22. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 22
LU-Decomposition
“Elementary operation” is for instance to multiply a row in the matrix
by a constant and add/subtract to/from another row
Elementary operations can be expressed as an operations matrix, M,
where MA=U. U is an upper triangular matrix. The original linear
equation Ax=b can then be written MAx=Ux=Mb=G. It can be
shown that the matrix M is lower triangular and so is the matrix M-1.
It is possible to write A=LU, where L=M-1, which means that the
matrix A has been decomposed in to L and U; A=LU
This is called triangular factorization or LU
factorization (or decomposition)

23. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 23
LU-Decomposition
⎡ a11 a12 a1n ⎤ ⎡l11 0 ′
0 ⎤⎡1 a12 ′
a1n ⎤
⎢a a22 ⎥ ⎢l
a1n ⎥ ⎢ 21 l22 0⎥ ⎥ ⎢0 1 ′ ⎥
a1n ⎥
⎢ 21 = ⎢
⎢ ⎥ ⎢ ⎥⎢ ⎥
⎢ ⎥ ⎢ ⎥⎢ ⎥
⎣an1 an 2 ann ⎦ ⎣ln1 ln 2 lnn ⎦⎣0 0 1⎦
A=LU

24. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 24
An Example of Crout’s Method of LU Decomposition
(4x4)
⎡ a11 a12 a13 a14 ⎤ ⎡l11 0 0 0 ⎤⎡1 u12 u13 u14 ⎤
⎢a a22 a23 a24 ⎥ ⎢l21 l22 0 0 ⎥ ⎢0 1 u23 u24 ⎥
⎢ 21 ⎥= ⎢ ⎥⎢ ⎥
⎢ a31 a32 a33 a34 ⎥ ⎢l31 l32 l33 0 ⎥ ⎢0 0 1 u34 ⎥
⎢ ⎥ ⎢ ⎥⎢ ⎥
⎣a41 a42 a43 a44 ⎦ ⎣l41 l42 l43 l44 ⎦⎣0 0 0 1⎦
a11 =l11 ⇒ l11 =a11
The 1st row of the L and a12 = l11u12 ⇒ u12 =
a12
U matrices on the right l11
side: a13 =l11u13 ⇒ u13 =
a13
l11
a14
a14 =l11u14 ⇒ u14 =
l11

25. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 25
An Example of Crout’s Method of LU Decomposition
(4x4) (2)
⎡ a11 a12 a13 a14 ⎤ ⎡l11 0 0 0 ⎤⎡1 u12 u13 u14 ⎤
⎢a a22 a23 a24 ⎥ ⎢l21 l22 0 0 ⎥ ⎢0 1 u23 u24 ⎥
⎢ 21 ⎥= ⎢ ⎥⎢ ⎥
⎢ a31 a32 a33 a34 ⎥ ⎢l31 l32 l33 0 ⎥ ⎢0 0 1 u34 ⎥
⎢ ⎥ ⎢ ⎥⎢ ⎥
⎣a41 a42 a43 a44 ⎦ ⎣l41 l42 l43 l44 ⎦⎣0 0 0 1⎦
a21 =l21 ⇒ l21 =a21
2nd row of the L a22 =l21u12 +l22 ⇒ l22 =a22 −l21u12
and U matrices [a23 −l21u13 ]
on the right side: a23 =l21u13 +l22 u23 ⇒ u23 =
l22
a24 =l21u14 +l22 u24 ⇒ u24 =
[a24 −l21u14 ]
l22

26. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 26
An Example of Crout’s Method of LU Decomposition (4x4)
(3)
⎡ a11 a12 a13 a14 ⎤ ⎡l11 0 0 0 ⎤⎡1 u12 u13 u14 ⎤
⎢a a22 a23 a24 ⎥ ⎢l21 l22 0 0 ⎥ ⎢0 1 u23 u24 ⎥
⎢ 21 ⎥= ⎢ ⎥⎢ ⎥
⎢ a31 a32 a33 a34 ⎥ ⎢l31 l32 l33 0 ⎥⎢0 0 1 u34 ⎥
⎢ ⎥ ⎢ ⎥⎢ ⎥
⎣a41 a42 a43 a44 ⎦ ⎣l41 l42 l43 l44 ⎦⎣0 0 0 1⎦
The 3rd row of a31 = l31 ⇒ l31 =a31
the L and U a32 = l31u12 +l32 ⇒ l32 =a32 −l31u12
matrices on a33 = l31u13 +l32 u23 +l33 ⇒ l33 = a33 −l31u13 −l32 u23
the right side: a34 = l31u14 +l32 u24 +l33u34 ⇒ u34 = [a34 −l31u14 −l32 u24 ]
1
l33

27. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 27
An Example of Crout’s Method of LU Decomposition (4x4)
(4)
⎡ a11 a12 a13 a14 ⎤ ⎡l11 0 0 0 ⎤⎡1 u12 u13 u14 ⎤
⎢a a22 a23 ⎥ ⎢l
a24 ⎥ ⎢ 21 l22 0 ⎥ ⎢0 1
0 ⎥⎢ u23 ⎥
u24 ⎥
⎢ 21 =
⎢ a31 a32 a33 a34 ⎥ ⎢l31 l32 l33 0 ⎥ ⎢0 0 1 u34 ⎥
⎢ ⎥ ⎢ ⎥⎢ ⎥
⎣a41 a42 a43 a44 ⎦ ⎣l41 l42 l43 l44 ⎦⎣0 0 0 1⎦
The 4th row of the
L and U matrices: Analogous formulas as before

28. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 28
An Example of Crout’s Method of LU Decomposition
- Order of Calculations
1 2
3 4
5 6
7 8
9 10
11 12
13 14

29. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 29
Crout’s Method of LU Decomposition - General
Equations for a n x n Matrix
⎫
lij = aij − ∑ lik ukj ; i ≥ j ; ⎪
k< j ⎪⎧ i = 1,2,
⎪ ,n
⎬⎨
(aij − ∑ lik ukj ) ⎪⎩ j = 1,2, ,n
; i< j ⎪
k< j
uij =
lii ⎪
⎭

30. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 30
Bi-factorization
lip = aip i> p
a pj
u pj = j> p
a pp
aip ⋅ a pj ⎫
a = aij −
'
ij ⎪
a pp ⎬i > p; j > p
aij = aij − lip ⋅ u pj
' ⎪
⎭

31. LDU Factorization Instead of LU-
Lecture 21 Power Engineering - Egill Benedikt Hreinsson 31
Factorization
⎡ a11 a12 a1n ⎤ ⎡ 1 0 0⎤ ⎡d11 0 ′
0 ⎤ ⎡1 a12 ′
a1n ⎤
⎢a a22 a1n ⎥ ⎢l21 1 0⎥ ⎢ 0 d 22 0 ⎥ ⎢0 1 a1n ⎥
′
⎢ 21 ⎥= ⎢ ⎥⋅⎢ ⎥⋅⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥
⎣an1 an 2 ann ⎦ ⎣ln1 ln 2 1⎦ ⎣ 0 0 d nn ⎦ ⎣0 0 1⎦
A=LDU

32. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 32
LDU-Factorization
d ( p)
p, p =a ( p)
p, p
ai(,p )
( p)
l
i, p = p
( p) i> p
a p, p
( p)
a
u ( p)
p, j = p, j
( p) j> p
a p, p
( p +1)
a ( p)
⋅a ( p)
⎫
⎪
=a − ⎬i > p og j > p
( p) i, p p, j
a i, j i, j
⎪
( p)
a p, p ⎭

33. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 33
Ieee 57 BUS TEST
CASE
Sparsity 93%

34. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 34
Ieee 57 BUS TEST CASE (Alternative ordering
of buses)
0
10
20
30
40
50
0 10 20 30 40 50
nz = 213

35. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 35
Software for power system analysis
• Powerworld (www.powerworld.com)
• Matpower
– (http://www.pserc.cornell.edu/matpower/)
• Eurostag www.eurostag.be
• EDSA www.edsa.com
• ETAP www.etap.com
• CYME www.cyme.com
• ASPEN www.aspeninc.com
• NEPLAN www.neplan.ch
• PSS/E, PSS/O http://www.pti-us.com
• DIGSILENT www.digsilent.de

36. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 36
Software for power system analysis (2)
• QuickStab® Professional www.scscc-us.com
• CAPE www.electrocon.com
• SKM Power* Tools www.skm.com
• DINIS www.dinis.com
• SPARD® www.energyco.com
• ESA Easy Power www.easypower.com
• DSA PowerTools www.powertechlabs.com
• SynerGEE www.advantica.biz
• SCOPE www.nexant.com

37. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 37
Software for power system analysis (3)
• CDEGS www.sestech.com
• ATP/EMTP http://www.emtp.org
• EMTP-RV www.emtp.com
• PSCAD/EMTDC www.pscad.com
• IPSA www.ipsa-power.com
• MiPower www.mipowersoftware.com
• Distribution Management System
(DMS) http://www.dmsgroup.co.yu/
• Optimal Aempfast http://www.otii.com/aempfast.html

38. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 38
Software for power system analysis (4)
• DEW http://www.samsix.com/dew.htm
• Simpow www.stri.se
• PSAT (Power System Analysis Toolbox)
http://thunderbox.uwaterloo.ca/~fmilano
• TRANSMISSION 2000 http://www.cai-
engr.com/T2000.htm
• POM tools (POM, OPM, BOR,...) for contingency analysis,
optimal mitigation measures, Boundary of operating
regions, stability,...etc http://www.vrenergy.com/
• Fendi : (free) http://www.martinole.org/Fendi/

39. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 39
Software for power system analysis (5)
• Anarede - load flow, Anafas - short circuit, Anatem -
electromechanical stability (Portúgalska)
http://www.cepel.br
• General Electric - PSLF,
http://www.gepower.com/prod_serv/products/utility_so
ftware/en/ge_pslf/index.htm
• Intellicon's Voltage Collapse Diagnostic and Postured
Control http://www.intellicon.biz
• Kína: Power System Analysis Software Package (PSASP):
http://www.psasp.com.cn
• MicroTran is the electromagnetic transients program
(EMTP) version of the University of British Columbia.
http://www.microtran.com

40. Lecture 21 Power Engineering - Egill Benedikt Hreinsson 40
Heimildir/tilvísanir
• W.F. Tinney, W.S. Meyer: “Solution of Large Sparse Systems by
Ordered Triangular Factorization”, IEEE Transactions on Automatic
control, Vol.AC-18, No 4, 1973, bls 333-346
• California Energy Commission Report, “WECC CAISO Specific Needs
for Loop Flow Monitoring, Management, Near Term Prediction and
Probabilistic Assessment, and Prototype Monitoring System Design”
Publication Number: CEC-500-2005-168, Publication Date:
NOVEMBER 2005
(http://www.energy.ca.gov/pier/final_project_reports/CEC-500-
2005-168.html)
• IEEE test systems:
http://www.ee.washington.edu/research/pstca/