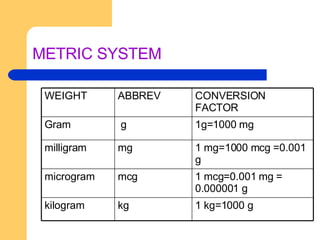
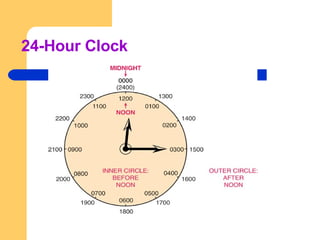
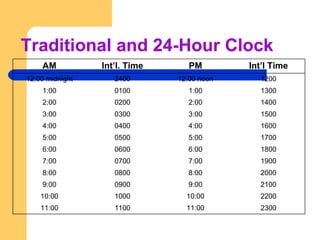
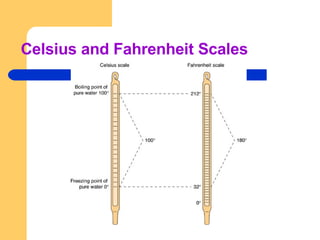
This document provides a basic math review of percentages, ratios, fractions, proportions, systems of measurement (metric, household, apothecary), and methods for calculating drug dosages. It defines key terms, outlines rules and formulas for conversions between different measurement systems and units, and provides examples of dosage calculations using ratio and proportion methods.

1. Basic Math Review Tyra L. Ousley, RN, MSN

15. METRIC SYSTEM WEIGHT ABBREV CONVERSION FACTOR Gram g 1g=1000 mg milligram mg 1 mg=1000 mcg =0.001 g microgram mcg 1 mcg=0.001 mg = 0.000001 g kilogram kg 1 kg=1000 g

24. Conversions for Other Clinical Applications: Time and Temperature Chapter 5

25. Time is an essential part of the drug order

26. What are some issues related to using the traditional time method?

27. 24-Hour Clock

28. Traditional and 24-Hour Clock AM Int’l. Time PM Int’l Time 12:00 midnight 2400 12:00 noon 1200 1:00 0100 1:00 1300 2:00 0200 2:00 1400 3:00 0300 3:00 1500 4:00 0400 4:00 1600 5:00 0500 5:00 1700 6:00 0600 6:00 1800 7:00 0700 7:00 1900 8:00 0800 8:00 2000 9:00 0900 9:00 2100 10:00 1000 10:00 2200 11:00 1100 11:00 2300

32. Celsius and Fahrenheit Scales

53. ANY QUESTIONS ????