This document discusses Boolean algebra and its application to sets and switching circuits. It begins by defining a Boolean algebra as a set with binary operations of sum and product satisfying certain properties like closure, commutativity, associativity, distributivity, identities, and complements. It then provides examples of Boolean algebras including the set {1,0} and sets closed under union and intersection. The document proceeds to cover topics like duality, basic theorems involving idempotent laws and De Morgan's laws, order relations, and an application to switching circuit design where circuits can be modeled as Boolean expressions.

1. Boolean Algebra and Sets
Set Theory

2. DEFINITION 1: A Boolean algebra is a set B with two binary operations sum (+, ∨, or ∪) and product (∗, ∧, or ∩)
suchthat:
B0.ClosureLaw
Forany 𝑎, 𝑏 ⋲B,thesum 𝑎 + 𝑏 andtheproduct 𝑎 ∗ 𝑏 existandareuniqueelementsinB.
B1.CommutativeLaw
𝑎 + 𝑏 = 𝑏 + 𝑎 and 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
B2.AssociativeLaw
𝑎 + 𝑏 + 𝑐) = 𝑎 + 𝑏)+ 𝑐 and 𝑎 ∗ 𝑏 ∗ 𝑐) = 𝑎 ∗ 𝑏)∗ 𝑐
B3.DistributiveLaw
𝑎 + 𝑏 ∗ 𝑐) = 𝑎 + 𝑏)∗ 𝑎 + 𝑐)and 𝑎 ∗ 𝑏 + 𝑐) = 𝑎 ∗ 𝑏)+(𝑎 ∗ 𝑐)
B4.Identity
Anadditiveidentity0andmultiplicativeidentity 𝑈 existsuchthatforany 𝑎 ⋲ 𝐵, 𝑎 +0 = 𝑎 and 𝑎 ∗ 𝑈 = 𝑎
B5.Complement
Forany 𝑎 ⋲ 𝐵 thereexists 𝑎′⋲ 𝐵 calledthecomplementof 𝑎 suchthat 𝑎 + 𝑎′
= 𝑈 and 𝑎 ∗ 𝑎′
= 0.
BOOLEAN ALGEBRA

3. 1.LetB={1,0} andlettwooperations+and∗bedefinedasfollows:
+ 1 0 ∗ 1 0
1 1 1 1 1 0
0 1 0 0 0 0
ThenB,ormorepreciselythetriplet(B,+,∗),isaBooleanalgebra.
2. Let 𝒜 be a family of sets that is closed under operation of union, intersection, and complement. Then 𝒜,∪,∩) is
aBooleanalgebra.
3.Let 𝓑thesetofpropositionsgeneratedbyvariables 𝑝, 𝑞,….Then(𝓑,∨,∧)isaBooleanalgebra.
EXERCISE:
Examples:
a. Show that Example 2 is a Boolean Algebra using sets A = {a, b, c} and set B = {d, e}.

4. Bydefinition,thedualofanystatementinaBooleanalgebra(B,+,∗)isthestatementthatisderivedby
interchanging+and∗,andtheiridentityelementsUand0,intheoriginalstatement
DUALITY IN BOOLEAN ALGEBRA
Example:
𝑈 + 𝑎) ∗ 𝑏 + 0 = 𝑏 0 ∗ 𝑎 + 𝑏 ∗ 𝑈 = 𝑏The dual of is
PrincipleofDuality:ThedualofanytheoreminaBooleanalgebraisalsoatheorem.
BASICTHEOREMS
THEOREM1(IdempotentLaw): 𝑖) 𝑎 +0 = 𝑎 𝑖𝑖) 𝑎∗ 𝑈 = 𝑎.
THEOREM2: 𝑖)A∪A’=U 𝑖𝑖)A∩A’=⌀.
THEOREM3(InvolutionLaw): 𝑎′)′
= 𝑎
THEOREM4: 𝑖) 𝑈′
= 0 𝑖𝑖)0′
= 𝑈
THEOREM5 DeMorgan’sLaw): 𝑖) 𝑎 + 𝑏)′
= 𝑎′
∗ 𝑏′ 𝑖𝑖) 𝑎∗ 𝑏)′
= 𝑎′
+ 𝑏′

5. Proof
*Prove Theorem 1 (Idempotent Law): 𝑖 𝑎 + 𝑎 = 𝑎 𝑖𝑖 𝑎 ∗ 𝑎 = 𝑎
Statement Reason𝑖𝑖)
𝑖) True by Principle of Duality.
EXERCISE:
1. Prove Theorem 2: 𝑖 𝑎 + 𝑈 = 𝑈 𝑖𝑖 𝑎 ∗ 0 = 0
2. Prove Theorem 4: 𝑖 𝑈′
= 0 𝑖𝑖 0′
= 𝑈
𝑎 = 𝑎 ∗ 𝑈 B4 Identity)
𝑎 = 𝑎 ∗ 𝑎 + 𝑎′) B5 Complement)
𝑎 = 𝑎 ∗ 𝑎 + 𝑎 ∗ 𝑎′) B3 Distributive)
𝑎 = 𝑎 ∗ 𝑎 + 0 B5 Complement)
𝑎 = 𝑎 ∗ 𝑎 B4 Identity)

6. ORDER IN BOOLEAN ALGEBRA
THEOREM6: Let 𝑎, 𝑏 ⋲ 𝐵,aBooleanalgebra.Thenthefollowingconditionsareequivalent:
(1) 𝑎 ∗ 𝑏′
= 0 (2)𝑎 + 𝑏 = 𝑏 (3)𝑎′
+ 𝑏 = 𝑈 (4)𝑎 ∗ 𝑏 = 𝑎
DEFINITION2:Let 𝑎,𝑏 ⋲ 𝐵,aBooleanalgebra.Then 𝑎 𝑝𝑟𝑒𝑐𝑒𝑑𝑒 𝑏,denotedby 𝑎 ≲ 𝑏,ifoneofthepropertiesin
Theorem6holds.
Examples:
1. Consider a Boolean algebra of sets 𝒜,∪,∩). Then A precedes B means that A⊂B. In other words, Theorem 6
statesthatifAisasubsetofB,thenthefollowingconditionshold:
1)A∩B’=⌀ 2)A∪B=B 3)A’∪B=U 4)A∩B=A
2.ConsideraBooleanalgebraofpropositions(𝓑,∨,∧).Thenpprecedesqmeansthatplogicallyimpliesq.

7. THEOREM7:TherelationinaBooleanalgebraBdefinedby 𝑎 ≲ 𝑏isapartialorderinB.
(1) 𝑎 ≲ 𝑎forevery 𝑎 ⋲ 𝐵 (ReflexiveLaw)
(2) 𝑎 ≲ 𝑏and 𝑏 ≲ 𝑎implies 𝑎 = 𝑏 (Anti-symmetricLaw)
(3) 𝑎 ≲ 𝑏and 𝑏 ≲ 𝑐implies 𝑎 ≲ 𝑐 (TransitiveLaw)
EXERCISE:
1. Prove Theorem 7

8. SWITCHING CIRCUITS DESIGNS
Let A, B, … denote electrical switches, and let A and A’ denote
switches with the property that if one is on then the other is
off, and vice versa. Two switches, say A and B, can be
connected by wire in a series or parallel combination as
follows:
A B
A
B
Series combination, A ∧ B Parallel combination, A ∨ B

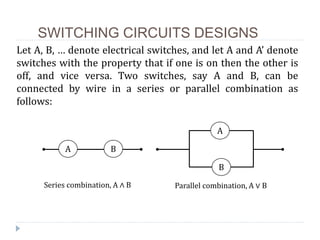
9. A Boolean switching circuit design means an arrangement of
wires and switches that can be constructed by repeated use
of series and parallel combinations; hence it can be
described by the use of connectives ∧ and ∨.
A
B
A’
C
A’
B
A B’
Circuit 2) A ∧ B’) ∨ [ A ∨ C) ∧ B]
Circuit 1) A ∧ B ∨ A’)

10. A B A ∧ B A B A ∨ B A A'
1 1 1 1 1 1 1 0
1 0 0 1 0 1 0 1
0 1 0 0 1 1
0 0 0 0 0 0
Now let 1 and 0 denote respectively, that a switch or a circuit is on and that
a switch or circuit is off.
*The tables describe the behavior of a series circuit A ∧ B, parallel circuit A ∨ B,
and the relationship between switch A and switch A’.
THEOREM 8: The algebra of Boolean switching circuits is a Boolean algebra.
EXERCISE:
1. Using circuit (1) in the example, when will the circuit be on and when will the
circuit be off?
2. Construct s circuit for (A ∨ B) ∧ C ∧ A’ ∨ B’ ∨ C’).

11. Reference:
Lipschuts, S. (2005). Schaums outline of theory and problem of set theory and
related topics. New York: McGraw-Hill Publishing Inc.
Thank you for listening.
Raymund T. de la Cruz
MAEd - Mathematics