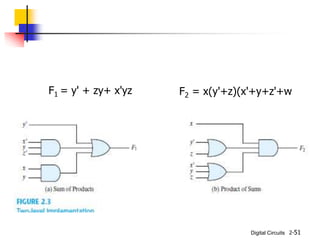
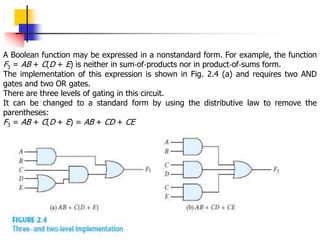
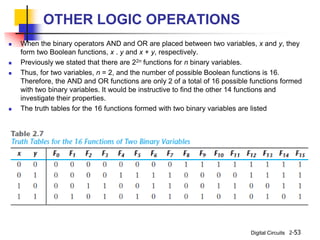
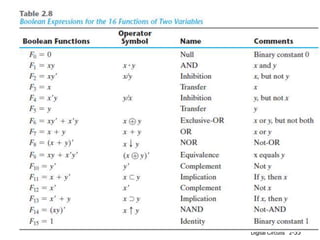
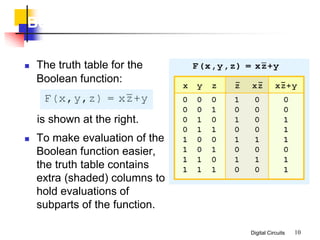
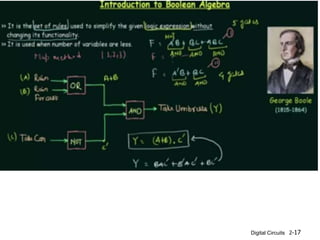
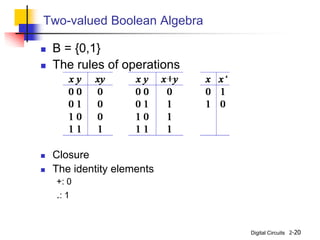
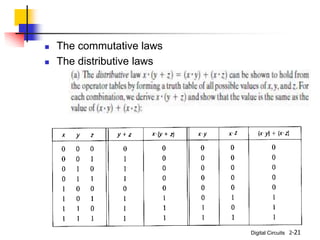
This document discusses Boolean algebra and its relationship to digital logic gates. It begins with an introduction to Boolean algebra, defined by George Boole in the 19th century as a mathematical system to represent logical thought. Boolean algebra uses two values (true/false, on/off, 1/0) and binary operators like AND, OR, and NOT. The document then provides the axiomatic definition of Boolean algebra, describing its basic elements, operators, and properties. Finally, it discusses two-valued Boolean algebra specifically and how it represents binary logic used in digital circuits.

1. Boolean Algebra and Logic Gates

2. Digital Circuits 2
Boolean Algebra and Digital Logic
Objectives
 Understand the relationship between Boolean logic
and digital computer circuits.

3. Digital Circuits
BOOLEAN ALGEBRA & LOGIC GATES
 Introduction,
 Basic definitions,
 Axiomatic definition of Boolean algebra,
 Basic theorems and properties of Boolean algebra,
 Boolean functions,
 Canonical and Standard Forms,
 Other Logic Operations,
 Digital logic gates
3

4. Digital Circuits 4
Introduction
 In the latter part of the nineteenth century, George
Boole incensed philosophers and mathematicians
alike when he suggested that logical thought could
be represented through mathematical equations.
 How dare anyone suggest that human thought could
be encapsulated and manipulated like an algebraic
formula?
 Computers, as we know them today, are
implementations of Boole’s Laws of Thought.
 John Atanasoff and Claude Shannon were among
the first to see this connection.

5. Digital Circuits 5
Introduction
 In the middle of the twentieth century, computers
were commonly known as “thinking machines” and
“electronic brains.”
 Many people were fearful of them.
 Nowadays, we rarely ponder the relationship
between electronic digital computers and human
logic. Computers are accepted as part of our lives.
 Many people, however, are still fearful of them.
 In this part, you will learn the simplicity that
constitutes the essence of the machine.

6. Digital Circuits 6
Boolean Algebra
 Boolean algebra is a mathematical system for
the manipulation of variables that can have
one of two values.
 In formal logic, these values are “true” and
“false.”
 In digital systems, these values are “on” and
“off,” 1 and 0, or “high” and “low.”
 Boolean expressions are created by
performing operations on Boolean variables.
 Common Boolean operators include AND, OR,
and NOT.

7. Digital Circuits 7
Boolean Algebra
 A Boolean operator can be
completely described using a
truth table.
 The truth table for the Boolean
operators AND and OR are
shown at the right.
 The AND operator is also known
as a Boolean product. The OR
operator is the Boolean sum.

8. Digital Circuits 8
Boolean Algebra
 The truth table for the
Boolean NOT operator is
shown at the right.
 The NOT operation is most
often designated by an
overbar. It is sometimes
indicated by a prime mark
( ‘ ) or an “elbow” ().

9. Digital Circuits 9
Boolean Algebra
 A Boolean function has:
• At least one Boolean variable,
• At least one Boolean operator, and
• At least one input from the set {0,1}.
 It produces an output that is also a member of
the set {0,1}.
Now you know why the binary numbering
system is so handy in digital systems.

10. Digital Circuits 10
Boolean Algebra
 The truth table for the
Boolean function:
is shown at the right.
 To make evaluation of the
Boolean function easier,
the truth table contains
extra (shaded) columns to
hold evaluations of
subparts of the function.

11. Digital Circuits
BASIC DEFINITIONS
 Boolean algebra, like any other deductive mathematical system, may be defined
with a set of elements, a set of operators, and a number of unproved axioms or
postulates.
 A set of elements is any collection of objects, usually having a common
property. x ∈ S, y ∉ S, A = {1, 2, 3, 4}.
 A binary operator defined on a set S of elements is a rule
 that assigns, to each pair of elements from S, a unique element from S. As an
example, consider the relation
a *b = c.
 * is a binary operator if it specifies a rule for finding c from the pair (a, b) and
also if a, b, c ∈ S. However, * is not a binary operator if a, b ∈ S, and if c ∉ S.
 The postulates of a mathematical system form the basic assumptions from
which it
 is possible to deduce the rules, theorems, and properties of the system.
 The most common postulates used to formulate various algebraic structures are
as follows:
11

12. Digital Circuits
1. Closure. A set S is closed with respect to a binary operator if, for every pair of
elements of S, the binary operator specifies a rule for obtaining a unique element
of S. For example, the set of natural numbers N = {1, 2, 3, 4, c} is closed with
respect to the binary operator + by the rules of arithmetic addition, since, for any
a, b ∈ N, there is a unique c ∈ N such that a + b = c. The set of natural numbers
is not closed with respect to the binary operator - by the rules of arithmetic
subtraction, because 2 - 3 = -1 and 2, 3 ∈ N, but (-1) ∉ N.
2. Associative law. A binary operator * on a set S is said to be associative
whenever (x * y) * z = x * (y * z) for all x, y, z, ∈ S.
3. Commutative law. A binary operator * on a set S is said to be commutative
whenever x * y = y * x for all x, y ∈ S.
4. Identity element. A set S is said to have an identity element with respect to a
binary operation * on S if there exists an element e ∈ S with the property that e *
x = x * e = x for every x ∈ S.
 Example: The element 0 is an identity element with respect to the binary operator + on the set of
integers I = {c, -3, -2, -1, 0, 1, 2, 3,c}, since x + 0 = 0 + x = x for any x ∈ I The set of natural
numbers, N, has no identity element, since 0 is excluded from the set.

13. Digital Circuits
5. Inverse. A set S having the identity element e with respect to a binary operator * is said to
have an inverse whenever, for every x H S, there exists an element y H S such that x * y = e.
 Example: In the set of integers, I, and the operator +, with e = 0, the inverse of an
element a is (-a), since a + (-a) = 0.
6. Distributive law. If * and # are two binary operators on a set S, * is said to be distributive
over # whenever x * (y . z) = (x * y) . (x * z).
The operators and postulates have the following meanings:
 The binary operator + defines addition.
 The additive identity is 0.
 The additive inverse defines subtraction.
 The binary operator . defines multiplication.
 The multiplicative identity is 1.
 For a 0, the multiplicative inverse of a = 1/a defines division (i.e., a . 1/a = 1 ).
 The only distributive law applicable is that of . over +:
a . (b + c) = (a . b) + (a . c)

14. Digital Circuits
AXIOMATIC DEFINITION OF BOOLEAN ALGEBRA
 In 1854, George Boole developed an algebraic system now called Boolean
algebra.
 In 1938, Claude E. Shannon introduced a two‐valued Boolean algebra called
switching algebra that represented the properties of bistable electrical switching
circuits.
 For the formal definition of Boolean algebra, we shall employ the postulates
formulated by E. V. Huntington in 1904.
 Boolean algebra is an algebraic structure defined by a set of elements, B, together
with two binary operators, + and . , provided that the following (Huntington)
postulates are satisfied:
1. (a) The structure is closed with respect to the operator +.
(b) The structure is closed with respect to the operator . .
2. (a) The element 0 is an identity element with respect to +; that is, x + 0 = 0 + x = x.
(b) The element 1 is an identity element with respect to . ; that is, x . 1 = 1 . x = x.
3. (a) The structure is commutative with respect to +; that is, x + y = y + x.
(b) The structure is commutative with respect to . ; that is, x . y = y . x.
4. (a) The operator . is distributive over +; that is, x . (y + z) = (x . y) + (x . z).
(b) The operator + is distributive over . ; that is, x + (y . z) = (x + y) . (x + z).
5. For every element x ∈ B, there exists an element x’ ∈ B (called the complement of x) such that
(a) x + x’ = 1 and (b) x . x’ = 0.
6. There exist at least two elements x, y ∈ B such that x ≠ y.
14

15. Digital Circuits
Comparing Boolean algebra with arithmetic and ordinary algebra (the field of real
numbers), we note the following differences:
1. Huntington postulates do not include the associative law. However, this law
holds for Boolean algebra and can be derived (for both operators) from the other
postulates.
2. The distributive law of + over . (i.e., x + (y . z) = (x + y) . (x + z) ) is valid for
Boolean algebra, but not for ordinary algebra.
3. Boolean algebra does not have additive or multiplicative inverses; therefore,
there are no subtraction or division operations.
4. Postulate 5 defines an operator called the complement that is not available in
ordinary algebra.
5. Ordinary algebra deals with the real numbers, which constitute an infinite set of
elements. Boolean algebra deals with the as yet undefined set of elements, B,
but in the two‐valued Boolean algebra defined next (and of interest in our
subsequent use of that algebra), B is defined as a set with only two elements, 0
and 1.
15

16. Digital Circuits
Two‐Valued Boolean Algebra
16

17. Digital Circuits 2-17

18. Digital Circuits 2-18
Boolean Algebra (E.V. Huntington, 1904)
 A set of elements B and two binary
operators + and .
1. Closure w.r.t. the operator + (.)
 x, y B 'x+y B
2. An identity element w.r.t. + (.)
2a. 0+x = x+0 = x
2b. 1.x = x.1= x
3. Commutative w.r.t. + (.)
3a. x+y = y+x
3b. x.y = y.x

19. Digital Circuits 2-19
4. 4a . is distributive over +: x.(y+z)=(x.y)+(x.z)
4b + is distributive over.: x+(y.z)=(x+y).(x+z)
5. " x  B, $ x'  B (complement of x)
5a. x+x'=1 and
5b. x.x'=0
6. $ at least two elements x, y B ' x ≠ y
 Note
 the associative law can be derived
 no additive and multiplicative inverses
 Complement

20. Digital Circuits 2-20
Two-valued Boolean Algebra
 B = {0,1}
 The rules of operations
 Closure
 The identity elements
+: 0
.: 1

21. Digital Circuits 2-21
 The commutative laws
 The distributive laws

22. Digital Circuits 2-22
 Complement
 x+x'=1: 0+0'=0+1=1; 1+1'=1+0=1
 x.x'=0: 0.0'=0.1=0; 1.1'=1.0=0
 Has two distinct elements 1 and 0, with 0 ≠ 1
 Note
 a set of two elements
 + : OR operation; . : AND operation
 a complement operator: NOT operation
 Binary logic is a two-valued Boolean algebra

23. Digital Circuits 2-23
Basic Theorems and Properties
 Duality
 the binary operators are interchanged; AND <-> OR
 the identity elements are interchanged; 1 <-> 0

24. Digital Circuits 2-24
• Theorem 1(a): x+x = x
x+x = (x+x) 1 by postulate: 2(b)
= (x+x) (x+x') 5(a)
= x+xx' 4(b)
= x+0 5(b)
= x 2(a)
– Theorem 1(b): x x = x
xx = x x + 0 2(a)
= xx + xx' 5(b)
= x (x + x') 4(a)
= x 1 5(a)
= x 2(b)

25. Digital Circuits 2-25
 Theorem 2 (a)
 x + 1 = 1 (x + 1) 2(b)
= (x + x')(x + 1) 5(a)
= x + x' 1 4(b)
= x + x' 5(b)
= 1 2(a)
 Theorem 2 (b)
 x 0 = 0 by duality
 Theorem 3: (x')' = x
 Postulate 5 defines the complement of x, x + x' = 1
and x x' = 0
 The complement of x' is x is also (x')'

26. Digital Circuits 2-26
 Theorem 6 (a)
 x + xy = x 1 + xy (2b)
= x (1 +y) (4a)
= x 1 (x+1=1)
= x (2b)
 Theorem 6 (a)
 x (x + y) = x by duality
 By means of truth table
x y xy x + xy
0 0 0 0
0 1 0 0
1 0 0 1
1 1 1 1

27. Digital Circuits 2-27
 DeMorgan's Theorems
 (x+y)' = x' y'
 (x y)' = x' + y'
x y x+y (x+y)‘ x‘ y‘ x‘y’
0 0 0 1 1 1 1
0 1 1 0 1 0 0
1 0 1 0 0 1 0
1 1 1 0 0 0 0

28. Digital Circuits 2-28
• Operator Precedence
– parentheses
– NOT
– AND
– OR
– examples
– x y' + z
– (x y + z)'

29. Digital Circuits
 Theorem: For every pair a, b in set B: (a+b)’ =
a’b’, and (ab)’ = a’+b’.
 Proof: We show that a+b and a’b’ are
complementary.
 In other words, we show that both of the following
are true (P5): (a+b)+(a’b’) = 1, (a+b)(a’b’) = 0.
Proof (Continue):
(a+b)+(a’b’)
=(a+b+a’)(a+b+b’) (P4)
=(1+b)(a+1) (P5)
=1 (Theorem 3)
2-29

30. Digital Circuits
 (a+b)(a’b’)
 =(a’b’)(a+b) (P3)
 =a’b’a+a’b’b(P4)
 =0*b’+a’*0 (P5)
 =0+0
 =0 (P2)
2-30

31. Digital Circuits 2-31
Boolean Functions
 A Boolean function expresses the logical relationship between binary
variables and is evaluated by determining the binary value of the expression
for all possible values of the variables.
 binary variables
 binary operators OR and AND
 unary operator NOT
 parentheses
 Examples
 F1= x y z'
 F2 = x + y'z
 F3 = x' y' z + x' y z + x y'
 F4 = x y' + x' z

32. Digital Circuits 2-32
 The truth table of 2n entries
 Two Boolean expressions may specify the same
function
 F3 = F4

33. Digital Circuits 2-33
• Implementation with
logic gates
• F4 is more economical

34. Digital Circuits 2-34
F1= x y z'
F2 = x + y'z
F3 = x' y' z + x' y z + x y'
F4 = x y' + x' z

35. Digital Circuits 2-35
Algebraic Manipulation
 To minimize Boolean expressions
 literal: a primed or unprimed variable (an input to a gate)
 term: an implementation with a gate
 The minimization of the number of literals and the number of terms =>
a circuit with less equipment
 It is a hard problem (no specific rules to follow)
 EXAMPLE 2.1 Simplify the following Boolean functions to a minimum
number of literals.
1. x(x'+y)
2. x+x'y
3. (x+y)(x+y')
4. xy + x’z + yz
5. (x + y)(x’ + z)(y + z)

36. Digital Circuits 2-36
1. x(x'+y) = xx' + xy = 0+ xy = xy
2. x+x'y = (x+x')(x+y) = 1 (x+y) = x+y
3. (x+y)(x+y') = x+xy+xy'+yy'
= x(1+y+y')
= x
4. xy + x'z + yz = xy + x'z + yz(x+x')
= xy + x'z + yzx + yzx'
= xy(1+z) + x'z(1+y)
= xy +x'z
5. (x+y)(x'+z)(y+z) = (x+y)(x'+z) by duality from the previous result
 x'y'z + x'yz + xy' = x'z(y'+y) + xy'
= x'z + xy'

37. Digital Circuits
Worksheet-2-1
2-37

38. Digital Circuits 2-38
Complement of a Function
 an interchange of 0's for 1's and 1's for 0's in the
value of F
 by DeMorgan's theorem
 (A+B+C)' = (A+X)' let B+C = X
= A'X' by DeMorgan's
= A'(B+C)'
= A'(B'C') by DeMorgan's
= A'B'C' associative
 generalizations
 (A+B+C+ ... +F)' = A'B'C' ... F'
 (ABC ... F)' = A'+ B'+C'+ ... +F'

39. Digital Circuits 2-39
 EXAMPLE 2.2 Find the complement of the functions F1= x’yz’ + x’y’z and F2
= x(y’z’ + yz). By applying DeMorgan’s theorems as many times as necessary,
the complements are obtained as follows:
 F1’= (x'yz' + x'y'z)' = (x'yz')' (x‘y'z)‘ = (x+y'+z) (x+y+z')
 F2’= [x(y'z'+yz)]' = x' + ( y'z'+yz)' = x' + (y'z')' (yz)‘ = x' + (y+z) (y'+z')
=x’+yz’+y’z
 EXAMPLE 2.3 Find the complement of the functions F1 and F2 of Example 2.2 by
taking their duals and complementing each literal.
 A simpler procedure
 take the dual of the function and complement each literal
 F1= x'yz' + x'y'z
the dual of F1 is (x'+y+z') (x'+y'+z)
complement each literal (x+y'+z)(x+y+z') = F1’

40. Digital Circuits 2-40
Canonical and Standard Forms
 Minterms and Maxterms
 A minterm: an AND term consists of all literals in
their normal form or in their complement form
 For example, two binary variables x and y,
 xy, xy', x'y, x'y'
 It is also called a standard product
 n variables con be combined to form 2n
minterms
 A maxterm: an OR term
 It is also call a standard sum
 2n
maxterms

41. Digital Circuits 2-41
 each maxterm is the complement of its
corresponding minterm, and vice versa

42. Digital Circuits 2-42
 An Boolean function can be expressed by
 a truth table
 sum of minterms
 f1 = x'y'z + xy'z' + xyz = m1 + m4 +m7
 f2 = x'yz+ xy'z + xyz'+xyz = m3 + m5 +m6 + m7

43. Digital Circuits 2-43
 The complement of a Boolean function
 the minterms that produce a 0
 f1' = m0 + m2 +m3 + m5 + m6
= x'y'z'+x'yz'+x'yz+xy'z+xyz'
 f1 = (f1')'
= (x+y+z)(x+y'+z) (x+y'+z') (x'+y+z')(x'+y'+z)
= M0 M2 M3 M5 M6
 Any Boolean function can be expressed as
 a sum of minterms
 a product of maxterms
 canonical form

44. Digital Circuits 2-44
Sum of minterms
 EXAMPLE 2.4 Express the Boolean function F = A + B’C as a sum
of minterms. The function has three variables: A, B, and C. The first
term A is missing two variables; therefore,
 F = A+B'C
= A (B+B') + B'C
= AB +AB' + B'C
= AB(C+C') + AB'(C+C') + (A+A')B'C
=ABC+ABC'+AB'C+AB'C'+A'B'C
 F = A'B'C +AB'C' +AB'C+ABC'+ ABC
= m1 + m4 +m5 + m6 + m7
 F(A,B,C) = S(1, 4, 5, 6, 7)
 or, built the truth table first

45. Digital Circuits 2-45

46. Digital Circuits 2-46
Product of maxterms
 Each of the 22n functions of n binary variables can be also expressed
as a product of maxterms.
 EXAMPLE 2.5:

47. Digital Circuits 2-47
Conversion between Canonical Forms
 Conversion between Canonical Forms
 F(A,B,C) = S(1,4,5,6,7)
 F'(A,B,C) = S(0,2,3)
 By DeMorgan's theorem
F(A,B,C) = P(0,2,3)
 mj' = Mj
 sum of minterms = product of maxterms
 interchange the symbols S and P and list those
numbers missing from the original form
 S of 1's
 P of 0's

48. Digital Circuits 2-48

49. Digital Circuits 2-49

50. Digital Circuits 2-50
Standard Forms
 Standard Forms
 Canonical forms are seldom used
 sum of products
F1 = y' + zy+ x'yz‘
 product of sums
F2 = x(y'+z)(x'+y+z'+w)
 F3 = A'B'CD+ABC'D'

51. Digital Circuits 2-51
F1 = y' + zy+ x'yz F2 = x(y'+z)(x'+y+z'+w

52. Digital Circuits 2-52
A Boolean function may be expressed in a nonstandard form. For example, the function
F3 = AB + C(D + E) is neither in sum‐of‐products nor in product‐of‐sums form.
The implementation of this expression is shown in Fig. 2.4 (a) and requires two AND
gates and two OR gates.
There are three levels of gating in this circuit.
It can be changed to a standard form by using the distributive law to remove the
parentheses:
F3 = AB + C(D + E) = AB + CD + CE

53. Digital Circuits
OTHER LOGIC OPERATIONS
 When the binary operators AND and OR are placed between two variables, x and y, they
form two Boolean functions, x . y and x + y, respectively.
 Previously we stated that there are 22n functions for n binary variables.
 Thus, for two variables, n = 2, and the number of possible Boolean functions is 16.
Therefore, the AND and OR functions are only 2 of a total of 16 possible functions formed
with two binary variables. It would be instructive to find the other 14 functions and
investigate their properties.
 The truth tables for the 16 functions formed with two binary variables are listed
2-53

54. Digital Circuits
 The 16 functions listed can be subdivided into three
categories:
1. Two functions that produce a constant 0 or 1.
2. Four functions with unary operations: complement and
transfer.
3. Ten functions with binary operators that define eight
different operations: AND, OR, NAND, NOR,
exclusive‐OR, equivalence, inhibition, and implication.
2-54

55. Digital Circuits 2-55

56. Digital Circuits 2-56
Digital Logic Gates
 Boolean expression: AND, OR and NOT
operations
 Constructing gates of other logic operations
 the feasibility and economy
 the possibility of extending gate's inputs
 the basic properties of the binary operations
 the ability of the gate to implement Boolean
functions

57. Digital Circuits 2-57

58. Digital Circuits 2-58
 Extension to multiple inputs
 A gate can be extended to multiple inputs
 if its binary operation is commutative and associative
 AND and OR are commutative and associative
 (x+y)+z = x+(y+z) = x+y+z
 (x y)z = x(y z) = x y z

59. Digital Circuits 2-59

60. Digital Circuits 2-60
 Multiple NOR = a complement of OR gate
 Multiple NAND = a complement of AND
 The cascaded NAND operations = sum of products
 The cascaded NOR operations = product of sums

61. Digital Circuits 2-61
 The XOR and XNOR gates are commutative and
associative
 Multiple-input XOR gates are uncommon?
 XOR is an odd function: it is equal to 1 if the inputs
variables have an odd number of 1's

62. Digital Circuits
Positive and Negative Logic- add on topic
2-62
Choosing the high‐level H to represent logic 1 defines a positive logic
system.
Choosing the low‐level L to represent logic 1 defines a negative logic
system.

63. Digital Circuits 2-63