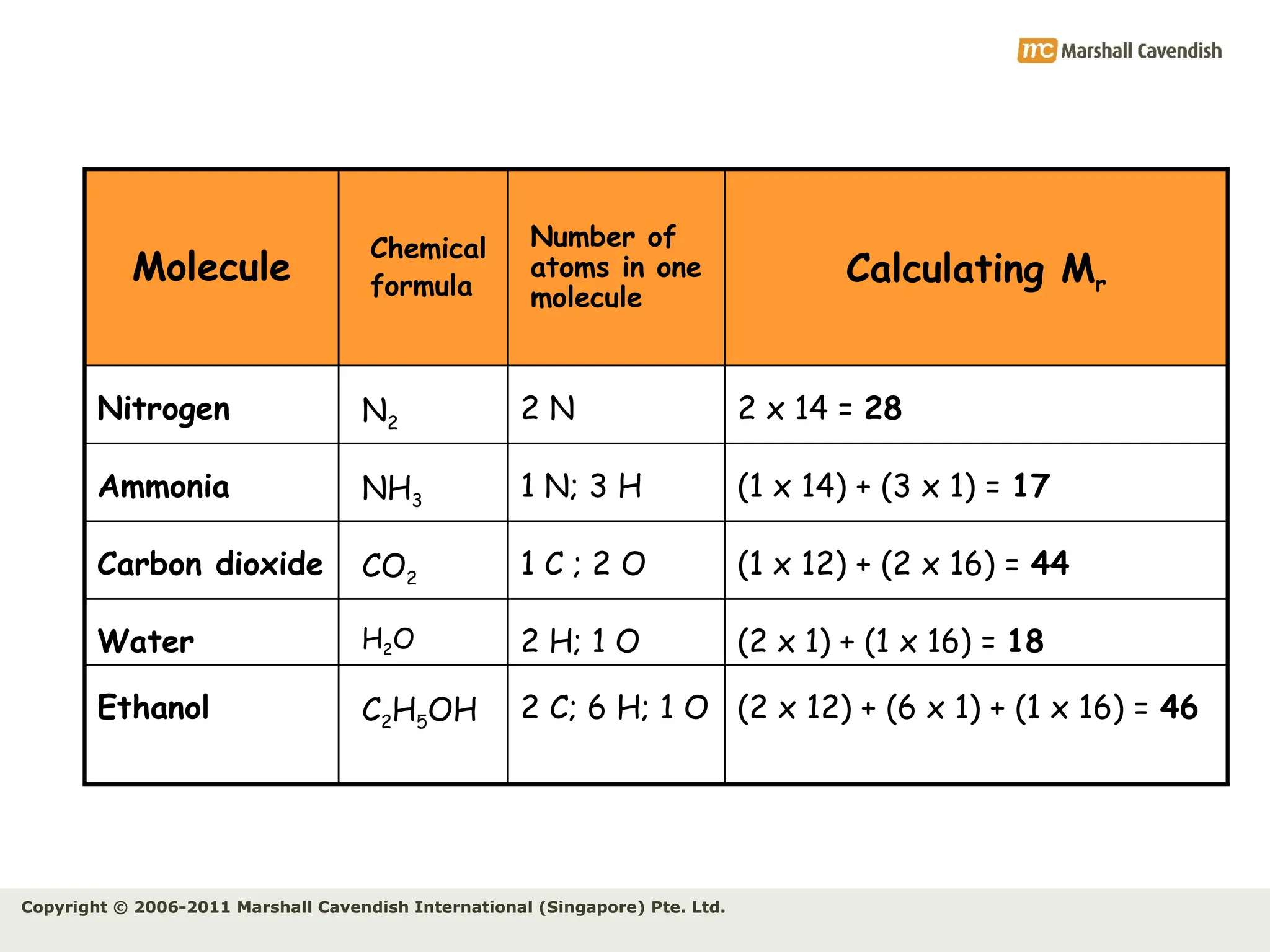
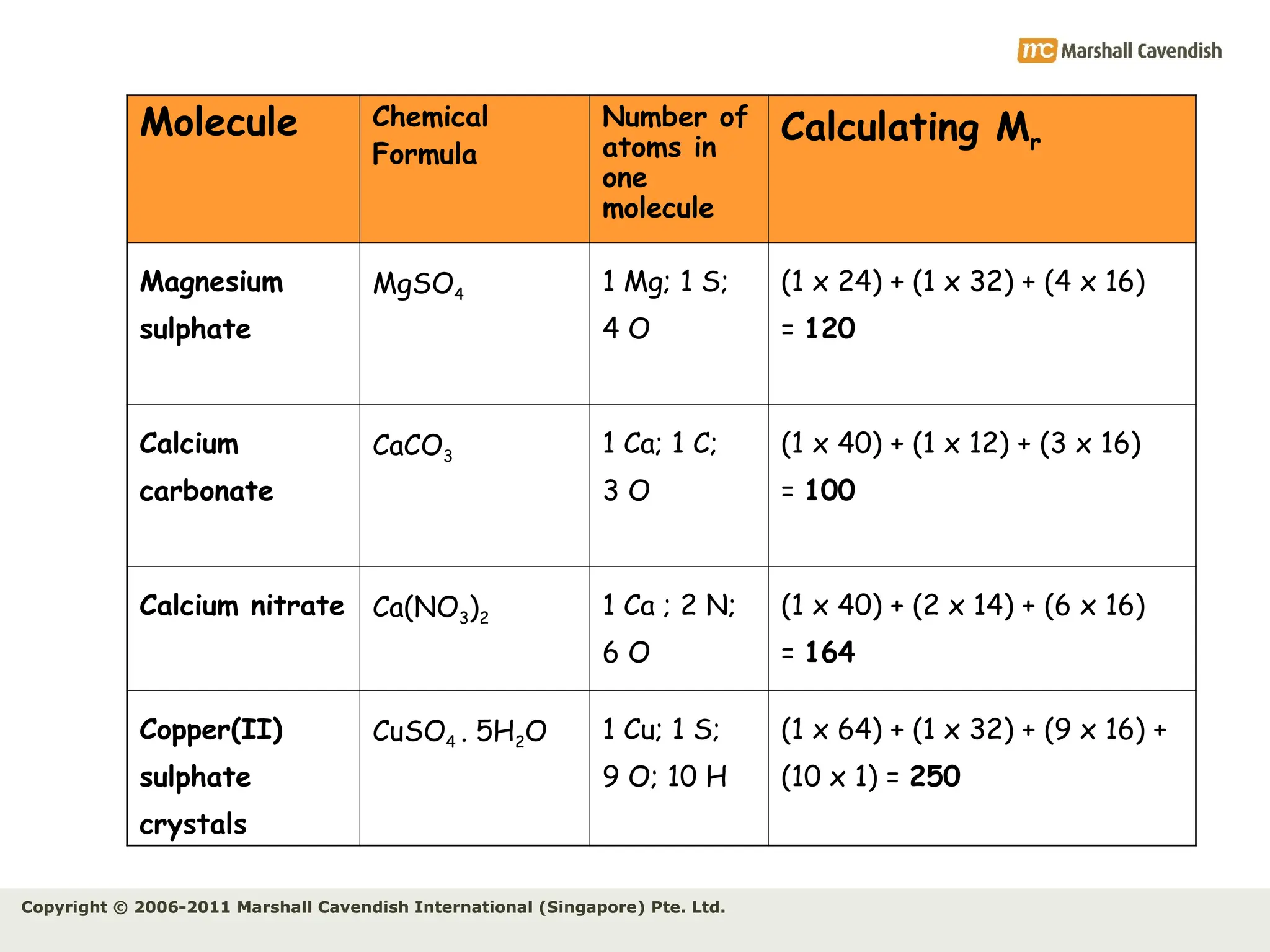
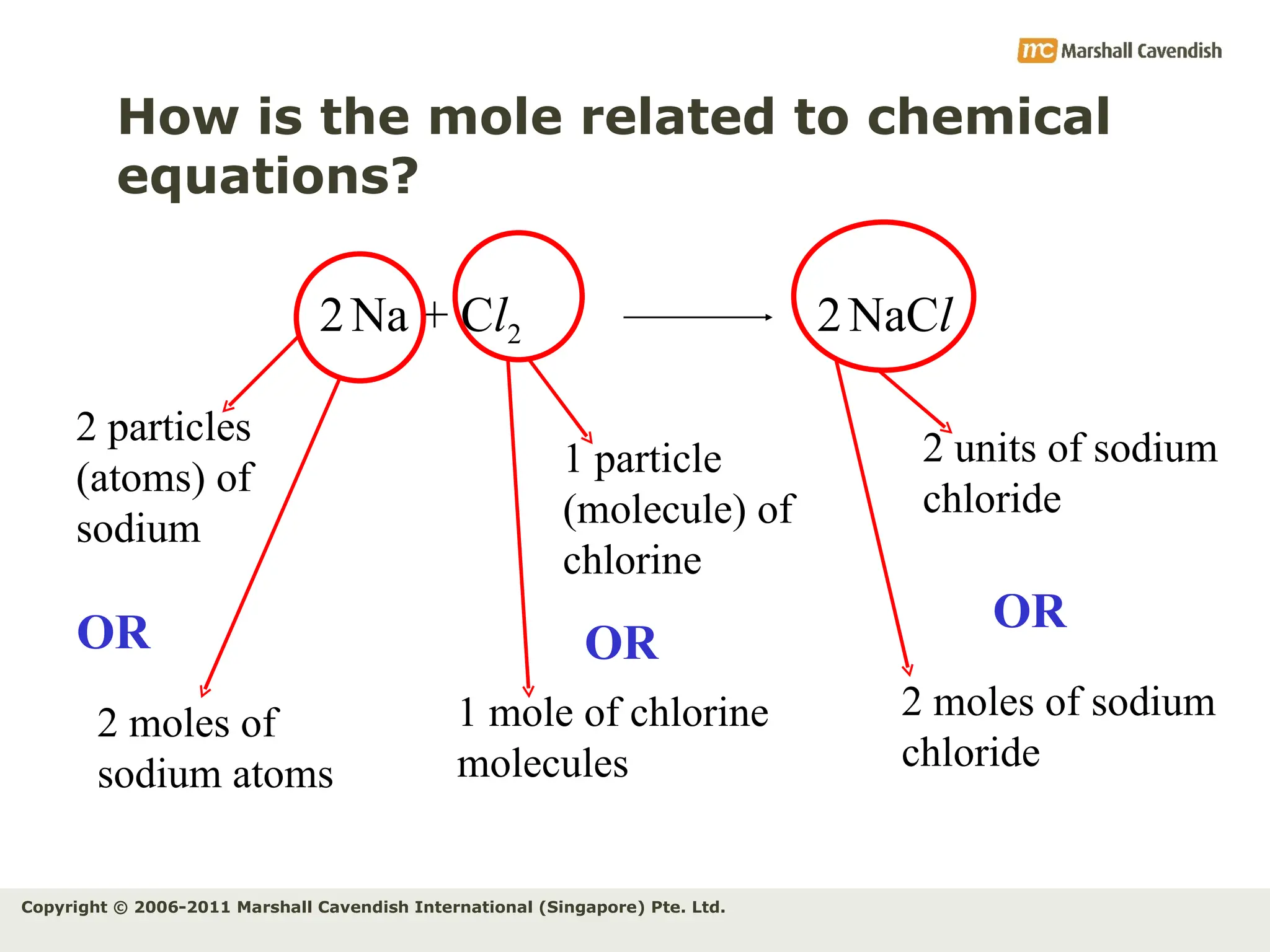
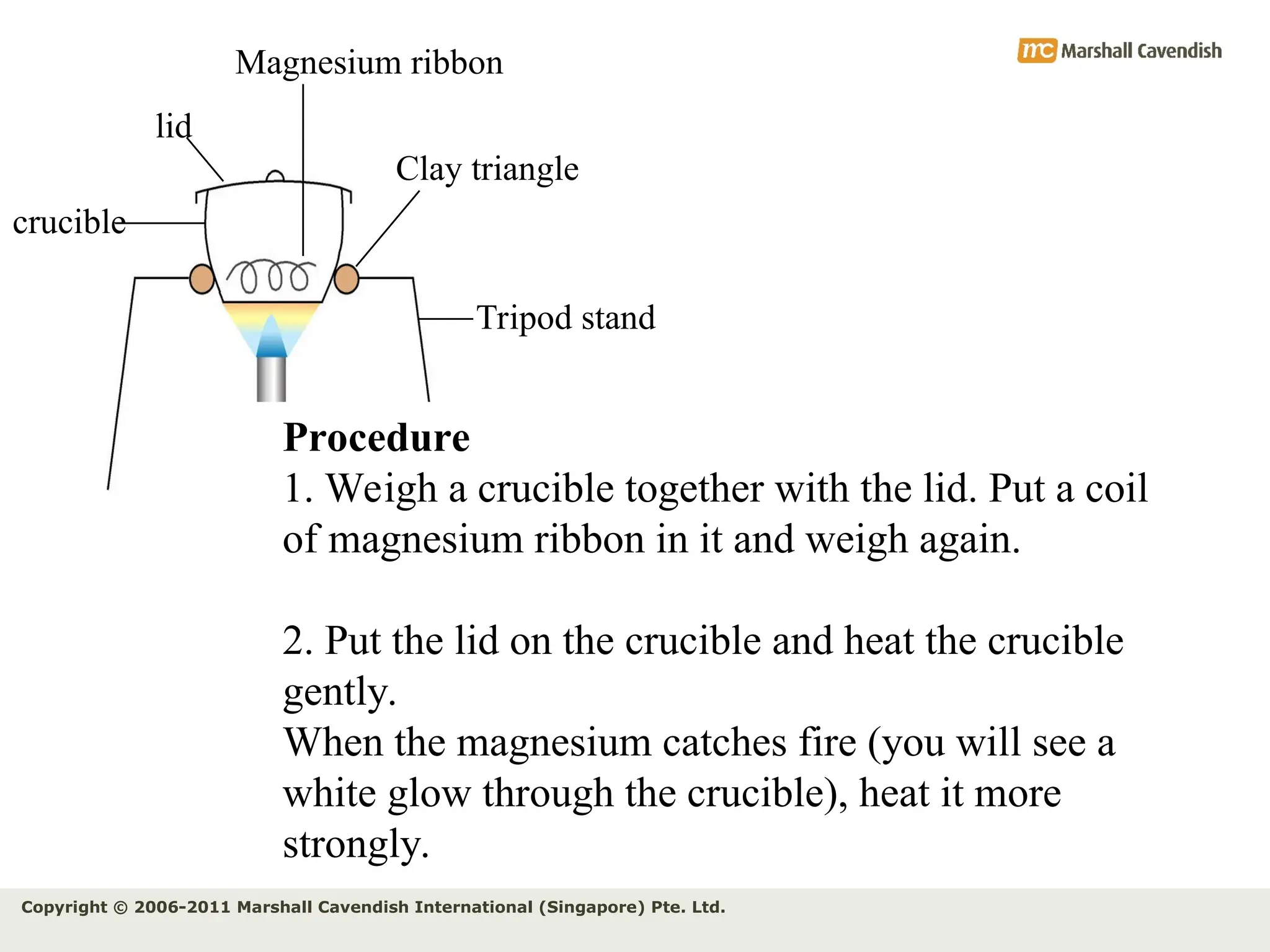
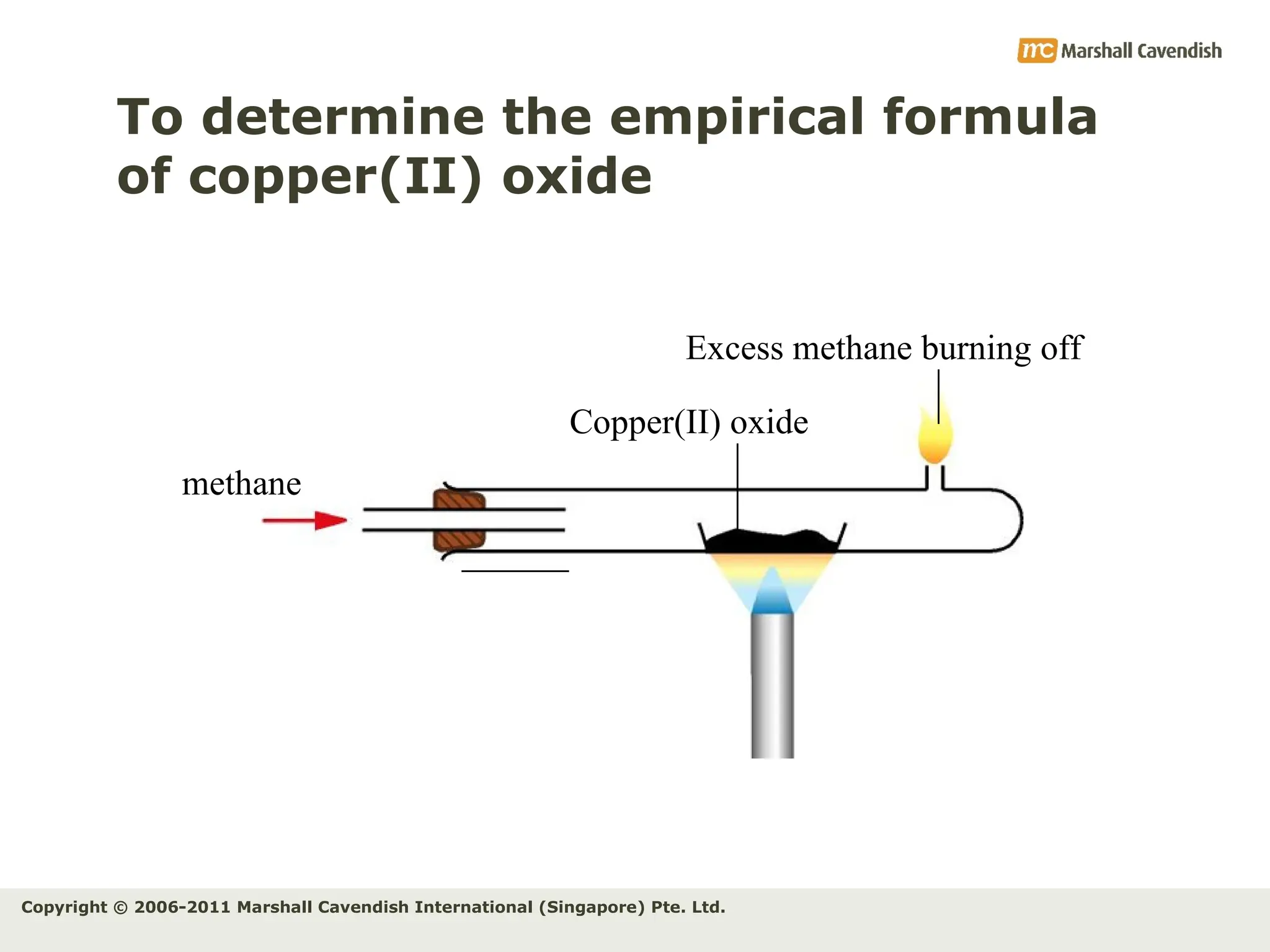
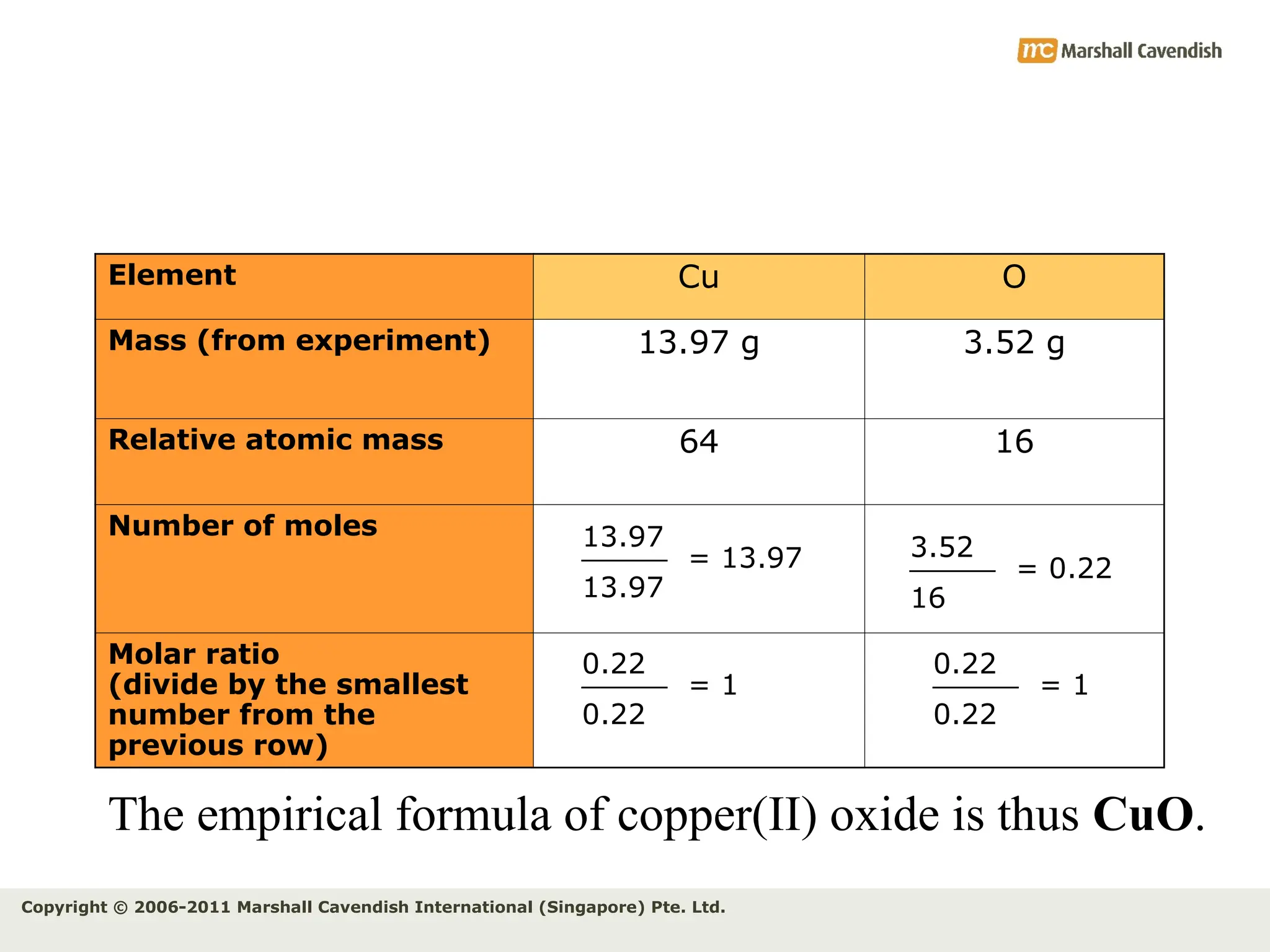
The document explains the concepts of relative atomic mass (Ar) and relative molecular mass (Mr), emphasizing their calculation and significance in chemistry. It details how these masses are derived using isotopes and provides examples for various compounds and elements. Additionally, it introduces the mole as a unit for measuring atomic quantities and discusses relationships between moles, particles, and molar mass.