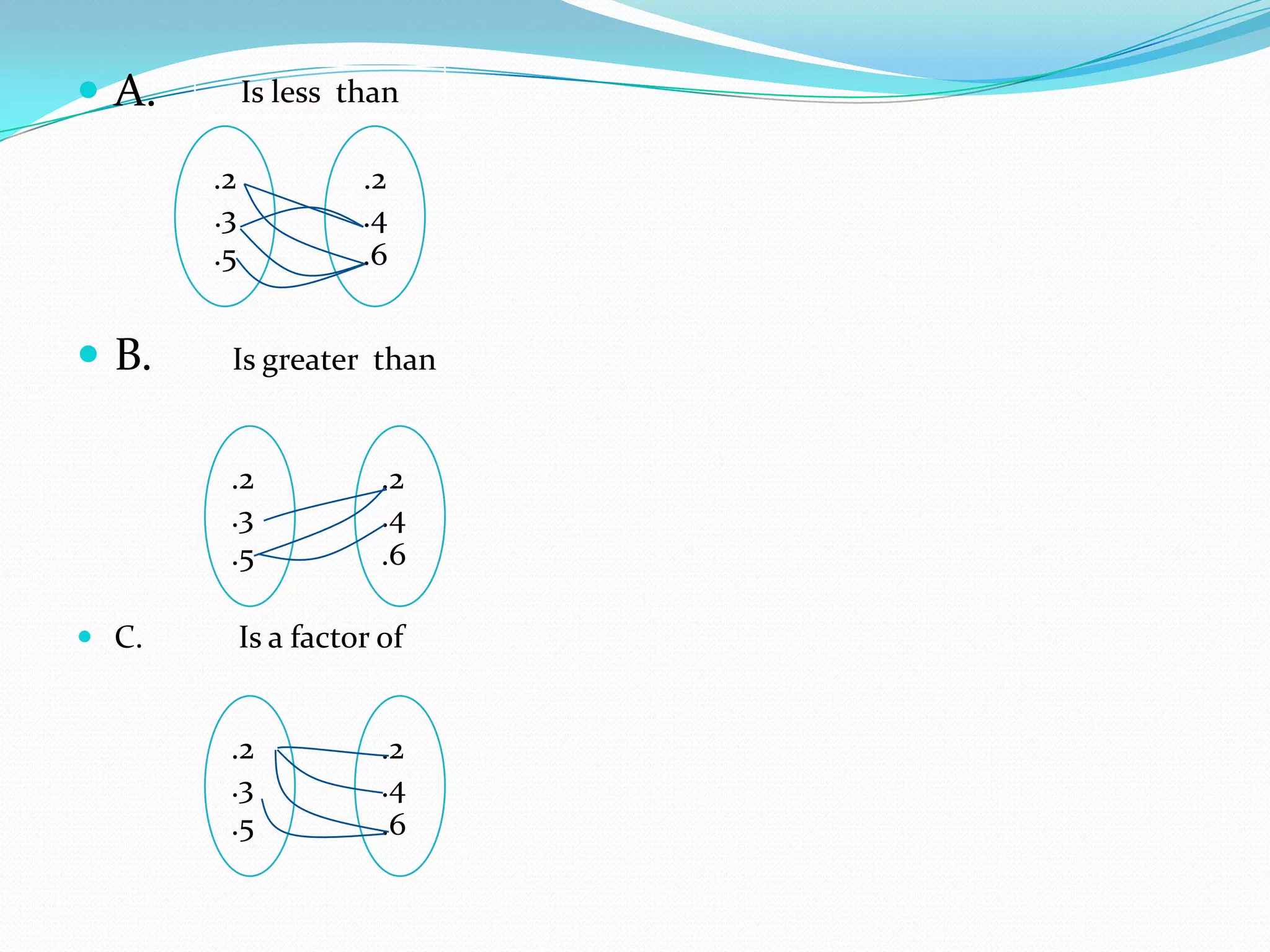
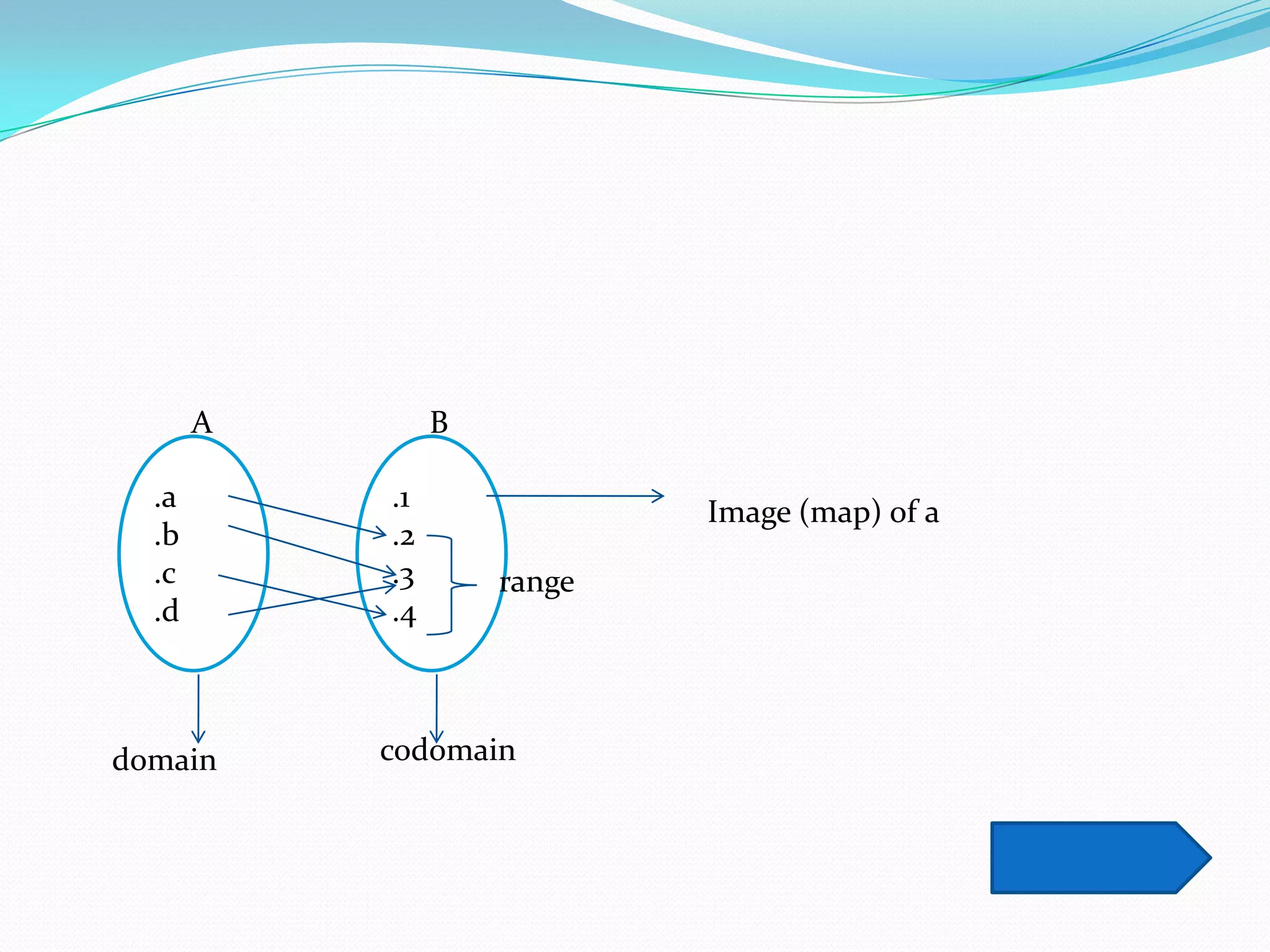
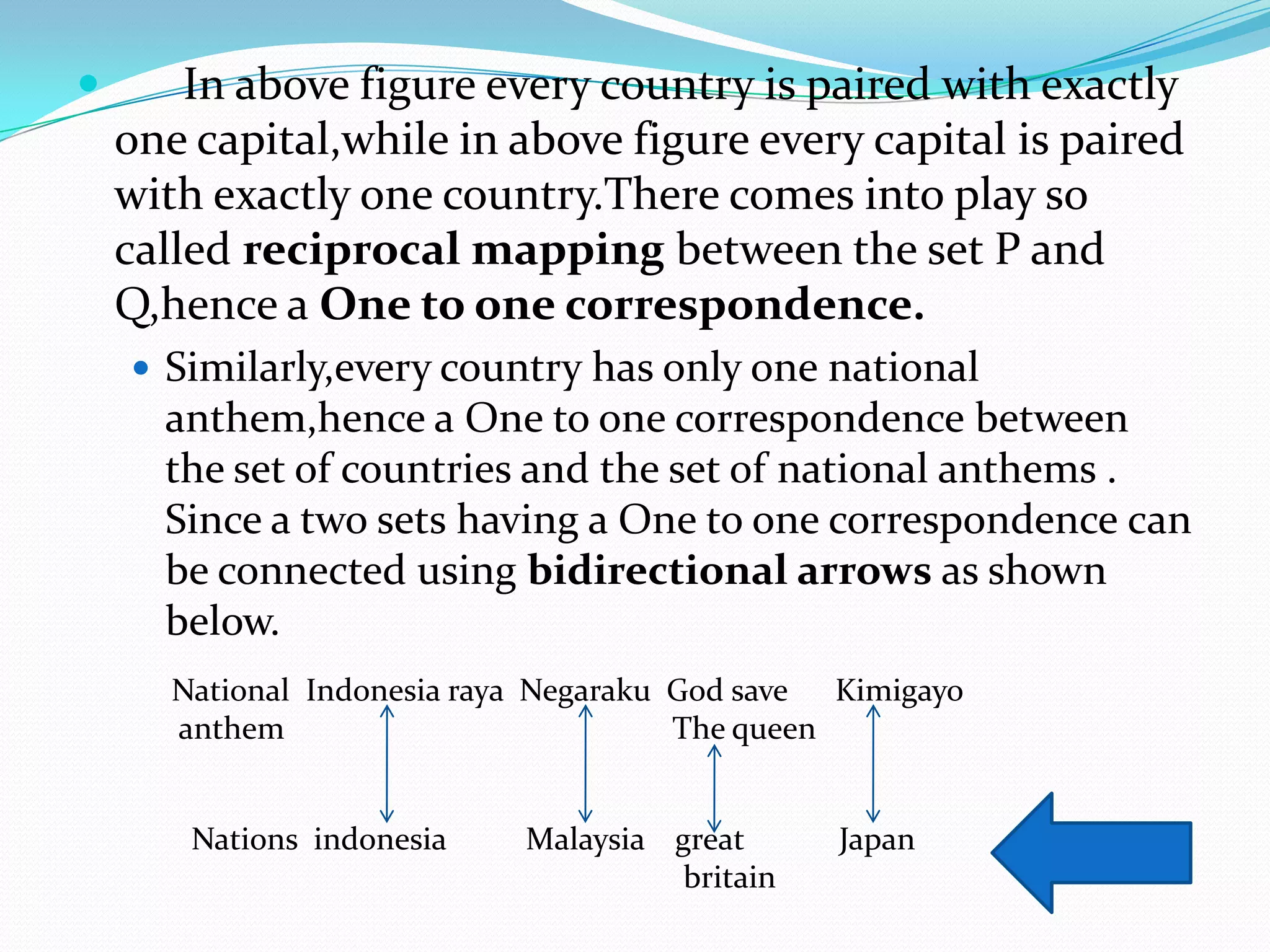
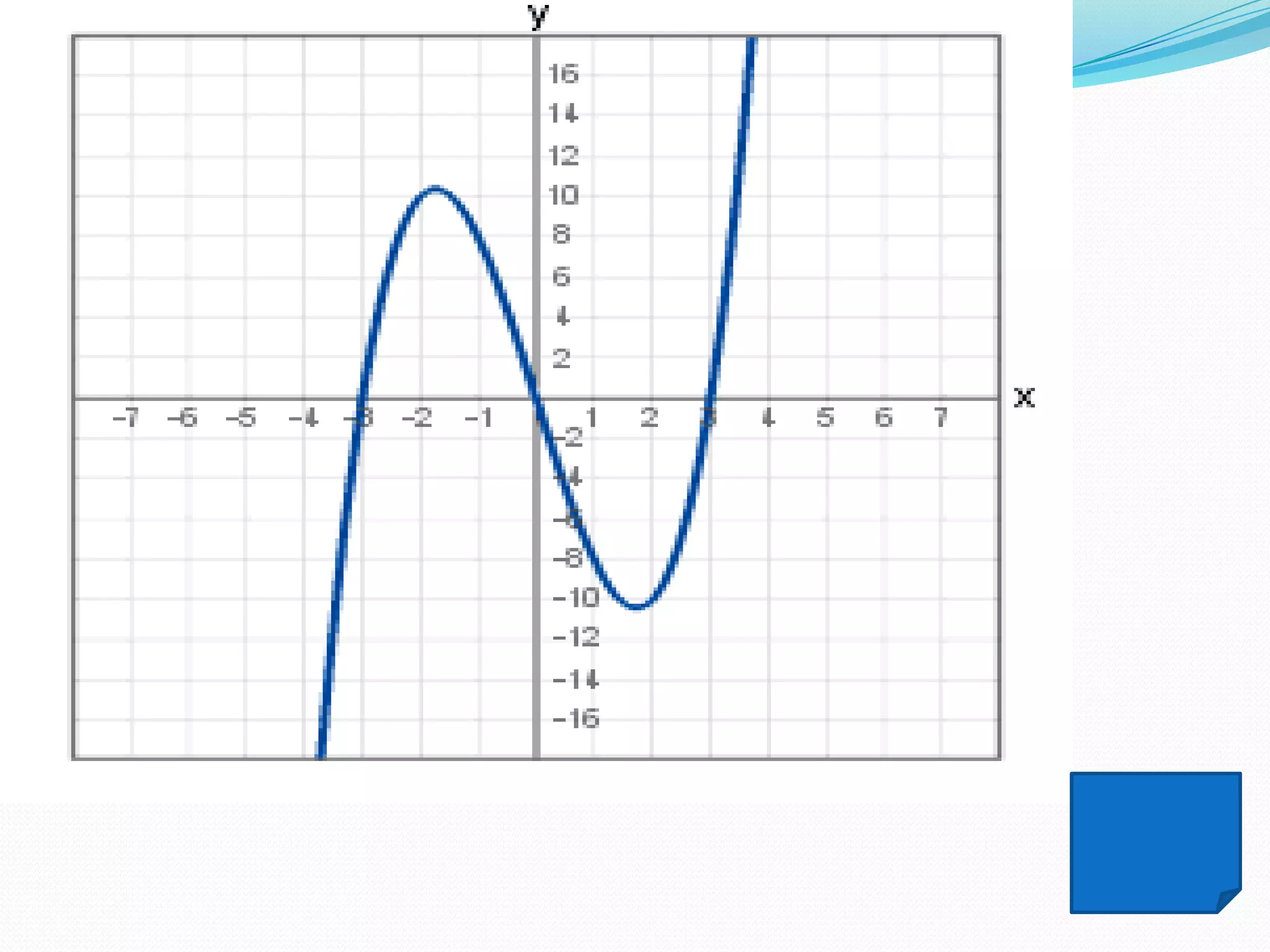
The document discusses functions and their properties. It defines a function as a special relation where each element of the domain is mapped to exactly one element of the range. Functions can be represented using arrow diagrams, Cartesian diagrams, or sets of ordered pairs. The number of possible mappings between two sets depends on the sizes of the sets. A one-to-one correspondence exists when each element of one set is paired with a unique element of the other set. A function formula expresses the relationship between an independent variable and dependent variable. The graph of a function consists of all the points (x, f(x)) where x is in the domain and f(x) is the image of x under the function.

1. M.Yafie Setyo W.
7.10/13

2. contens
 Understanding relations
 Function of mapping
 One-to-one correspondence
 Function formula
 Graph of a functions

3. Understanding relations
 Explanation
 Expressing relations

4. explanation
 Ria and Reni like hp
 Reni and Revi likes samsung
 Rian like lenovo
if a={Ria, Reni, Revi, Rian} and b={hp, samsung, lenovo}
a relation among the element of the set b can be build.
Figure 1.0
Ria Hp relation
Reni Samsung
Revi Lenovo
Rian The relation from set a and set b
visualized in figure 1.0 is called a
favor relation.

5. Expressing relations
 Arrow diagram
 Cartesian diagram
 Sets of ordered pairs

6. Arrow diagram
 example:
Build three types of relation from the set P={2,3,5} to the
set Q={2,4,6} and express them using arrow diagram.

7.  A. Is less than
.2 .2
.3 .4
.5 .6
 B. Is greater than
.2 .2
.3 .4
.5 .6
 C. Is a factor of
.2 .2
.3 .4
.5 .6

8. From the example,What is arrow
diagram?????
 A relation is represented by Arrow.
Is less than
.2 .2
.3 .4
.5 .6

9. Cartesian diagram
 The relation among the element of two sets A of B can
be expressed by a cartesian diagram in which the
element of the set A acting as the first set lie on
horizontal axis and the element of the set B acting as
the second set lie on vertical axis .
Figure 1.1
Cartesian
diagram
A.
2.

10. Sets of the ordered pairs
 A relation among the element of two sets K and L can
be expressed as an ordered pairs(x,y) in which x e K
and y e L is Paired

11. Function of mapping
 Understanding function of mappings
 Expressing function or mappings
 Number of possible ways of mapping between two sets

12. Understanding function of mappings
Let A and B be any two non-empty sets. Let A = {p, q,
r} and B = {a, b, c, d}. Suppose by some rule or other,
we assign to each element of A a ‘unique’ element of
B. Let p be associated to a, q be associated to b, r be
associated to c etc. The set {(p, a), (q, b), (r, c) } is
called a function from set A to set B. If we denote this
set by ‘f’ then we write f : A ® B which is read as "f " is
a function of A to B or ‘f’ is a mapping from A to B.

13. example
 Determine whether or not the following arrow
diagram express mapping.
B B A B
A A
.a .u .u .u
.a .a
.b .v .v .v
.b .b
.c .w .w .w
.c .c
.x .x .x
1 2 3

14. Answer is…….
 Figure 1. does not express a mapping since there exits
an element of A,namely b,which is paired with more
than one element of B.
 Figure 2. does express a mapping since every element
of A paired with exactly one element of B.
 Figure 3. does not express a mapping since there exits
an element of A,namely b,which is paired with no
element of B.

15. A B
.a .1 Image (map) of a
.b .2
.c .3 range
.d .4
domain codomain

16. explanation
 A={a,b,c,d} is called domain
 B={1,2,3,4} is called codomain
 {2,3,4} which called range , is set of the elements of Q
are paired with the elements of P.
 That element a is paired with 2 can be denoted by a-
2,which is read “ a is mapped to 2" in the form of a-2.2
called the image or map from a.

17. Expressing function or mappings
 In previous section we have stated that function is a
special relation.therefore,a function can be expressed
by means of any of the following three expressions.
 1. arrow diagram
 2.cartesian diagram
 3.Sets of ordered pairs

18. Number of possible ways of
mapping between two sets
 1 possible (A={a,b} to B={p})
.a
.p
.b
 2.possible (A={a} to B={p,q})
.a .a
.p .p
.q .q

19.  8 possible (A={a,b,c} to B={p,q} )
.a .a
.p .p .a
.b .b .p
.q .q .b
.c .c .q
.c
.a .a .a
.p .p .p
.b .b .b
.q .q .q
.c .c .c
.a .a
.p .p
.b .b
.q .q
.c .c

20.  9 possible (A={a,b} B={p,q,r})
.a
.p .a .a
.b .p
.q .b .b .p
.q .q
.r
.r .r
.a
.b .p .a
.q .b .p .a
.q .b .p
.r
.r .q
.r
.a .a .a
.b .p .p .p
.b .b
.q .q .q
.r .r .r

21. One to one correspondence
P P
Q Q
Indonesia. Jakarta. Jakarta. Indonesia.
Malaysia. Kuala lumpur. Kuala Malaysia.
Thailand. Bangkok. lumpur. Thailand.
Singapore. Singapore. Bangkok. Singapore.
philipine Manila. Singapore. philipine
Manila.

22.  In above figure every country is paired with exactly
one capital,while in above figure every capital is paired
with exactly one country.There comes into play so
called reciprocal mapping between the set P and
Q,hence a One to one correspondence.
 Similarly,every country has only one national
anthem,hence a One to one correspondence between
the set of countries and the set of national anthems .
Since a two sets having a One to one correspondence can
be connected using bidirectional arrows as shown
below.
National Indonesia raya Negaraku God save Kimigayo
anthem The queen
Nations indonesia Malaysia great Japan
britain

23. Functions Formula
 Formulating functions
 Independent variable and dependent Variable

24. Formulating functions
 A mapping by a function f that maps every element x of a
set A to an element y of a set can be denoted by.
 f:x y
 The notation f : x y is read:function f maps x to y. here
,y is called the image (map) of x under f
 Figure 2.0 shows a functions f mapping A to B. if x an
element of the domain of A,then the image of x under f is
denoted by f(x),and is read a function of x.
 Image 2.1 describes the mapping f:x x+2.Since the
image of x under f can be denoted by f(x),we can express
the mapping as f(x) =x+2.
 The form f(x)=x+2 is called function formula.

25. Figure
x f(x) 2.0
x x+2 Figure 2.1

26. example
 Determine the function formula for each the following
functions.
 Functions f:x 4x+1
 Answer;
 f:x 4x+1,is formulated as f(x)=4x+1

27. Independent variable and
dependent Variable
 Dependent:A variable that depends on one or more
other variables. For equations such as y = 3x – 2, the
dependent variable is y. The value of y depends on the
value chosen for x. Usually the dependent variable is
isolated on one side of an equation. Formally, a
dependent variable is a variable in an
expression, equation, or function that has its value
determined by the choice of value(s) of other
variable(s).

28.  Independent: A variable in an equation that may have its
value freely chosen without considering values of any other
variable. For equations such as y = 3x – 2, the independent
variable is x. The variable y is not independent since it
depends on the number chosen for x.
 Formally, an independent variable is a variable which can
be assigned any permissible value without any restriction
imposed by any other variable.

29. Graph of a function
 The graph of a function f is the set of all points in the
plane of the form (x, f(x)). We could also define the
graph of f to be the graph of the equation y = f(x). So,
the graph of a function if a special case of the graph of
an equation.

30. example
 Let f(x) = x2 - 3.
 Recall that when we introduced graphs of equations we
noted that if we can solve the equation for y, then it is easy to
find points that are on the graph. We simply choose a
number for x, then compute the corresponding value of y.
Graphs of functions are graphs of equations that have been
solved for y!
 The graph of f(x) in this example is the graph of y = x2 - 3. It is
easy to generate points on the graph. Choose a value for the
first coordinate, then evaluate f at that number to find the
second coordinate. The following table shows several values
for x and the function f evaluated at those numbers.
x -2 -1 0 1 2
F(x) 1 -2 -3 -2 1
 Each column of numbers in the table holds the coordinates
of a point on the graph of f.

31. Example 2
 Functions of one variable
 The graph of the function.
 Is {(1,a), (2,d), (3,c)}.

The graph of the cubic polynomial on the real line
 is
 {(x, x3-9x) : x is a real number}.If this set is plotted on a
Cartesian plane, the result is a curve (see figure).

33. Exercise
1. A B
.1 .2
.2 .4
.3 .6
The arrow diagram shown above expresses a……relations
A.is more than
B.is less than
C.is the square of
D.is a factor of

34.  2. P= {3,4,5} and Q= {1,2,3,4,5,6,7}.
 The set of ordered pairs which expresses the relation “is two
more than” from the set of P to the set of Q is....
A.{(3,2),(4,2),(5,2)}
B.{(3,4),(4,5),(5,6)}
C.{(3, 1),(4,2),(5,3)}
D.{(3, 5),(4,6),(5,7)}
3. i ii iii iv
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
Among the arrow diagram shown a.(i) and (ii)
b.(i) and (iii)
Above,those which express
c.(ii) and (iii)
Functions are… d.(ii) and (iv)

35.  4.
a. .p The range of the
.b .q function expressed by
c. .r the arrow diagram
shown is……
a. {p,r}
b. {a,b,c}
c. {p,q,r}
d. {a,b,c,p,q}
 5.Among the following sets of ordered
 (i) {(a,1),(a,2),(a,3),(a,4)} Those which have a one
 (ii) {(a,2),(a,2),(a,2),(a,2)} to one correspondence
are….
 (iii) {(a,1),(b,2),(c,1),(d,2)} a.(i)
b. (ii)
 (iv) {(a,1),(b,2),(c,3),(d,4)} c. (iii)
d. (iv)

36. 1.build a arrow diagram expressing the relation “is a factor”
from the set K=(0,1,2) to the setL=(4,5,6)
2.build an arrow diagram for each possible specification of
one to one correspondence between the set P={1,2} and the
set Q={a,b}
3.A={letter forming word”pandai”}
B={letter forming word”babat””}
Determine the number the number of possible ways of
mappings.
a.From A to B
b.From B to A
4.A relation on the set A={0,2,4,6,8} is expressed by x is
evenly divided by y where x,y A, express the relation as a
set of ordered pairs (x,y)!
5.Let the function f:x 2x+1
Build a table for the function f from{-3,-2,-1,0,1,2,3,4}to the set
of integers!

37. Thank you