Download as PDF, PPTX
Uploaded byPaulino Silva
Reciprocal Allocation Method
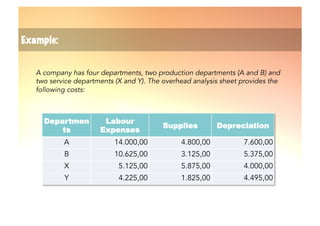
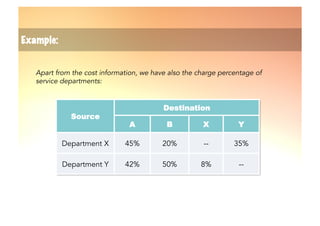
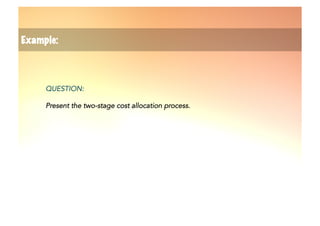
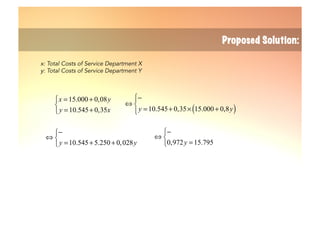
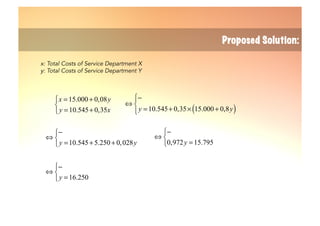
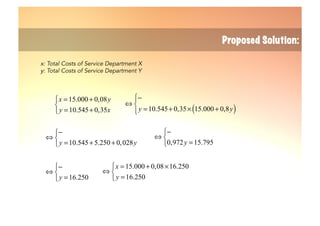
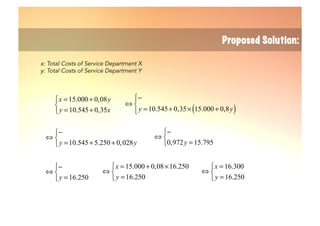
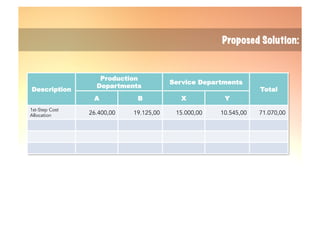
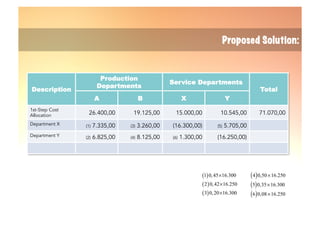
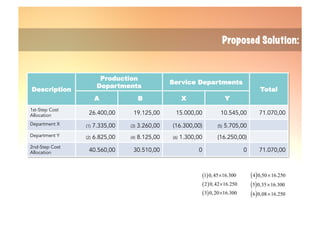
The document explains the reciprocal allocation method used in management accounting for distributing indirect costs among departments, specifically addressing the challenges posed by reciprocal charges between service departments. Through a detailed example involving four departments, it outlines a two-step cost allocation process, including the elimination of reciprocal charges and the final allocation of costs. The document provides formulas and calculations for determining the total costs for each department involved.
More Related Content
Reciprocal Allocation Method
- 1. HOW TO USETHE RECIPROCAL ALLOCATION METHOD By Paulino Silva
- 2. Introduction: As part ofmanagement accounting, the use of departmental cost allocation method for assigning indirect costs, despite its old origins, it is still widely used today.
- 3. Introduction: One of theproblems in using departmental cost allocation method, is the existence of reciprocal charges between service departments. Through a practical example we will see how to solve this problem.
- 4. Departmen ts Labour Expenses Supplies Depreciation A 14.000,004.800,00 7.600,00 B 10.625,00 3.125,00 5.375,00 X 5.125,00 5.875,00 4.000,00 Y 4.225,00 1.825,00 4.495,00 Example: A company has four departments, two production departments (A and B) and two service departments (X and Y). The overhead analysis sheet provides the following costs:
- 5. Source Destination A B XY Department X 45% 20% -- 35% Department Y 42% 50% 8% -- Example: Apart from the cost information, we have also the charge percentage of service departments:
- 6. QUESTION: Present the two-stagecost allocation process. Example:
- 7. 1st STEP: Elimination ofreciprocal charges. Proposed Solution:
- 8. x: Total Costsof Service Department X y: Total Costs of Service Department Y Proposed Solution:
- 9. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 10. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ ⇔ − y = 10.545+ 0,35× 15.000 + 0,8y( ) ⎧ ⎨ ⎪ ⎩⎪ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 11. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ 10.545 5.250 0,028y y −⎧ ⇔ ⎨ = + +⎩ ⇔ − y = 10.545+ 0,35× 15.000 + 0,8y( ) ⎧ ⎨ ⎪ ⎩⎪ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 12. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ 10.545 5.250 0,028y y −⎧ ⇔ ⎨ = + +⎩ ⇔ − 0,972y = 15.795 ⎧ ⎨ ⎩ ⇔ − y = 10.545+ 0,35× 15.000 + 0,8y( ) ⎧ ⎨ ⎪ ⎩⎪ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 13. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ 10.545 5.250 0,028y y −⎧ ⇔ ⎨ = + +⎩ ⇔ − 0,972y = 15.795 ⎧ ⎨ ⎩ ⇔ − y = 10.545+ 0,35× 15.000 + 0,8y( ) ⎧ ⎨ ⎪ ⎩⎪ ⇔ − y = 16.250 ⎧ ⎨ ⎩ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 14. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ 10.545 5.250 0,028y y −⎧ ⇔ ⎨ = + +⎩ ⇔ − 0,972y = 15.795 ⎧ ⎨ ⎩ ⇔ x = 15.000 + 0,08×16.250 y = 16.250 ⎧ ⎨ ⎩ ⇔ − y = 10.545+ 0,35× 15.000 + 0,8y( ) ⎧ ⎨ ⎪ ⎩⎪ ⇔ − y = 16.250 ⎧ ⎨ ⎩ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 15. x = 15.000+ 0,08y y = 10.545+ 0,35x ⎧ ⎨ ⎩ 10.545 5.250 0,028y y −⎧ ⇔ ⎨ = + +⎩ ⇔ − 0,972y = 15.795 ⎧ ⎨ ⎩ ⇔ x = 15.000 + 0,08×16.250 y = 16.250 ⎧ ⎨ ⎩ ⇔ − y = 10.545+ 0,35× 15.000 + 0,8y( ) ⎧ ⎨ ⎪ ⎩⎪ ⇔ x = 16.300 y = 16.250 ⎧ ⎨ ⎩ ⇔ − y = 16.250 ⎧ ⎨ ⎩ Proposed Solution: x: Total Costs of Service Department X y: Total Costs of Service Department Y
- 16. 2nd STEP: Two-stage costallocation process. Proposed Solution:
- 17. Description Production Departments Service Departments Total A BX Y Proposed Solution:
- 18. Description Production Departments Service Departments Total A BX Y 1st-Step Cost Allocation 26.400,00 19.125,00 15.000,00 10.545,00 71.070,00 Proposed Solution:
- 19. Description Production Departments Service Departments Total A BX Y 1st-Step Cost Allocation 26.400,00 19.125,00 15.000,00 10.545,00 71.070,00 Department X (1) 7.335,00 (3) 3.260,00 (16.300,00) (5) 5.705,00 Department Y (2) 6.825,00 (4) 8.125,00 (6) 1.300,00 (16.250,00) ( ) ( ) ( ) 1 0,45 16.300 2 0,42 16.250 3 0,20 16.300 × × × 4( )0,50 ×16.250 5( )0,35×16.300 6( )0,08×16.250 Proposed Solution:
- 20. Description Production Departments Service Departments Total A BX Y 1st-Step Cost Allocation 26.400,00 19.125,00 15.000,00 10.545,00 71.070,00 Department X (1) 7.335,00 (3) 3.260,00 (16.300,00) (5) 5.705,00 Department Y (2) 6.825,00 (4) 8.125,00 (6) 1.300,00 (16.250,00) 2nd-Step Cost Allocation 40.560,00 30.510,00 0 0 71.070,00 ( ) ( ) ( ) 1 0,45 16.300 2 0,42 16.250 3 0,20 16.300 × × × 4( )0,50 ×16.250 5( )0,35×16.300 6( )0,08×16.250 Proposed Solution:
- 21.