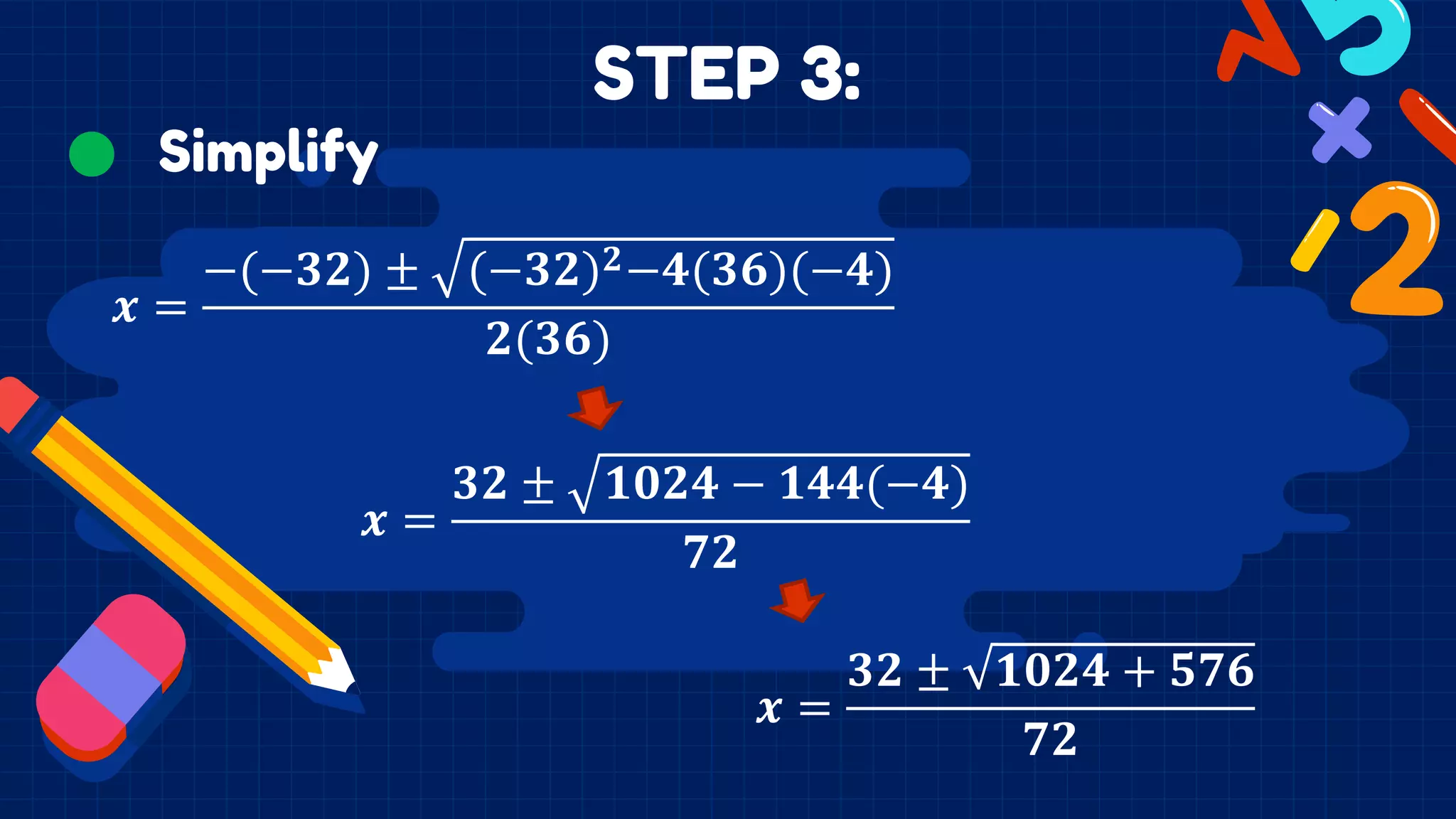
The document explains the concept of rational equations, which are equations that contain at least one fraction with polynomial numerators and denominators. It outlines step-by-step methods to solve these equations, including finding the least common denominator (LCD), multiplying by the LCD, simplifying, and checking for extraneous roots. Examples and detailed calculations illustrate the process, concluding that valid solutions exist as long as denominators are not zero.

1. 4th Quarter
Performance Task
Rational Equation
BY: LOURENZO MANIMTIM

2. SOLVING RATIONAL
EQUATIONS

3. —William Paul Thurston
“Mathematics is not about
numbers, equations, computations,
or algorithms it is about
UNDERSTANDING.”

4. What are Rational
Equations?
01

5. Rational Equations
In short terms, A rational equation is an equation
with one or more rational expressions. Containing
at least one fraction whose numerator and
denominator are polynomials.

6. What are some examples of Rational
Equations?
𝑥
5
−
1
4
=
𝑥
2
3 𝑦 + 3
𝑦 + 1
+ 3 =
3𝑦 ⊢ 1
4 + 1
𝑥
2
+
3𝑥
5
=
𝑥 − 1
4
𝑥 − 2
2𝑥
−
𝑥
𝑥 + 1
=
4 1 − 𝑥
6𝑥
• Take note that a rational equation is an equation that have two
or more Rational Expressions or a polynomial on its numerator
and denominator.

7. How to solve
Rational
Equations?
02

8. How to solve Rational Equations?
• To solve rational equations you will need to follow
these (4) four steps:
Find the LCD
Multiply everything by the LCD
Simplify
Checking of Answers

9. In this problem, we will solve this
3-R. expression, rational equation.
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥

10. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
First, we would need to find the LCD of our
equation.

11. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
To find the LCD we must search for terms with
the least similar multiplies found in the
denominator.

12. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
In our case, the common terms found in this
equation will be 9x.

13. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
Why? Because in the multiples of 3x and 9x. If
you will interpret their common factor.

14. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
9x, would become their common factors or in
other terms the LCD.

15. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
But what would happen with the polynomial 8x +1?

16. STEP 1:
Find the LCD
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
Since it is a binomial, it is not applicable to find the
LCD because it has no similar expressions present.

17. STEP 1:
Find the LCD
9x (8x+1)(
4𝑥
8𝑥+1
+
14
3𝑥
=
46
9𝑥
)
So instead, we would copy the binomial and place it
beside the LCD of 3x and 9x.

18. STEP 2:
Multiply everything by the LCD
9x (8x+1)(
4𝑥
8𝑥+1
+
14
3𝑥
=
46
9𝑥
)
To multiply we can use the distributive property or
cancellation.

19. STEP 2:
Multiply everything by the LCD
9x (8x+1)(
4𝑥
8𝑥+1
+
14
3𝑥
=
46
9𝑥
)
To multiply we can use the distributive property or
cancellation.

20. STEP 2:
Multiply everything by the LCD
9x (8x+1)(
4𝑥
8𝑥+1
+
14
3𝑥
=
46
9𝑥
)
But to answer our problem we will be using the
cancellation method because it is easier and faster.

21. STEP 2:
Multiply everything by the LCD
9x (8x+1)(
4𝑥
8𝑥+1
+
14
3𝑥
=
46
9𝑥
)
To Cancel, cancel the denominators with similar or
factor terms

22. STEP 2:
Multiply everything by the LCD
4𝑥
9x
+
14
3x(8x + 1)
=
46
8x + 1
After cancelling you will multiply the denominator to
the numerator.

23. STEP 2:
Multiply everything by the LCD
(9x)(4x) + 3(8x+1)(14) = 46 (8x +1)
Rewrite the terms and then multiply.

24. STEP 3:
36x2 + 336x + 42 = 368x + 46
After multiplying, you will now simplify the equation
firstly by transposition or the transfer of terms to
another.
Simplify
36x2 + 336x -368x -46 + 42= 0

25. STEP 3:
After transposing the terms we will be going to
combine the like terms.
Simplify
36x2 + 336x -368x -46 + 42= 0
36x2 -32x -4 = 0

26. STEP 3:
Now, we got our answer from combining like terms.
Usually, the answer will the equal to x but if the
answer shows to be a quadratic equation.
Simplify
36x2 -32x -4 = 0

27. STEP 3:
Simplify
To solve a quadratic equation, we are going to be
using the Quadratic Formula.
36x2 -32x -4 = 0
𝒙 =
−𝒃 ± 𝒃𝟐 − 𝟒𝒂𝒄
𝟐𝒂

28. STEP 3:
Simplify
Substitute the terms of ax2 + bx + c = 0, to the
formula and then simplify.
36x2 -32x -4 = 0
𝒙 =
−(−𝟑𝟐) ± (−𝟑𝟐)𝟐−𝟒(𝟑𝟔)(−𝟒)
𝟐(𝟑𝟔)

29. STEP 3:
Simplify
𝒙 =
−(−𝟑𝟐) ± (−𝟑𝟐)𝟐−𝟒(𝟑𝟔)(−𝟒)
𝟐(𝟑𝟔)
𝒙 =
𝟑𝟐 ± 𝟏𝟎𝟐𝟒 − 𝟏𝟒𝟒(−𝟒)
𝟕𝟐
𝒙 =
𝟑𝟐 ± 𝟏𝟎𝟐𝟒 + 𝟓𝟕𝟔
𝟕𝟐

30. STEP 3:
Simplify
𝒙 =
𝟑𝟐 ± 𝟏𝟔𝟎𝟎
𝟕𝟐
𝒙 =
𝟑𝟐 ± 𝟒𝟎
𝟕𝟐
𝒙𝟏 =
𝟑𝟐 + 𝟒𝟎
𝟕𝟐
𝒙𝟏 =
𝟕𝟐
𝟕𝟐
𝒙𝟏 = 𝟏
𝒙𝟐 =
𝟑𝟐 − 𝟒𝟎
𝟕𝟐
𝒙𝟐 =
−𝟖
𝟕𝟐
𝒙𝟐 = −
𝟏
𝟗

31. STEP 4:
Checking of Answers
After doing the Quadratic Formula and got our
answer, in this part we will going to be checking if
our solution is TRUE or FALSE (extraneous root)
𝒙𝟏 = 𝟏 𝒙𝟐 = −
𝟏
𝟗

32. STEP 4:
Checking of Answers 𝒙𝟏 = 𝟏
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
To check our answers, we will be going to
substitute the value of x and then simplify the
equation.
4(1)
8(1) + 1
+
14
3(1)
=
46
9(1)

33. STEP 4:
Checking of Answers 𝒙𝟏 = 𝟏
4(1)
8(1) + 1
+
14
3(1)
=
46
9(1)
4
9
+
14
3
=
46
9
4
9
+
42
9
=
46
9
46
9
=
46
9
𝑻𝒉𝒆 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒊𝒔
𝑻𝑹𝑼𝑬

34. STEP 4:
Checking of Answers
4𝑥
8𝑥 + 1
+
14
3𝑥
=
46
9𝑥
To check our answers, we will be going to substitute the
value of x and then simplify the equation.
4(−
1
9
)
8(−
1
9
) + 1
+
14
3(−
1
9
)
=
46
9(−
1
9
)
𝒙𝟐 = −
𝟏
𝟗

35. STEP 4:
Checking of Answers
𝑻𝒉𝒆 𝒆𝒒𝒖𝒂𝒕𝒊𝒐𝒏 𝒊𝒔
𝑻𝑹𝑼𝑬
𝒙𝟐 = −
𝟏
𝟗
−
4
9
8(−
1
9
) + 1
+
14
3(−
1
9
)
=
46
9(−
1
9
)
−
4
9
1
9
+
14
−
3
9
=
46
−1
−4 + −42 = −46 −46 = −46

36. CONCLUSION
 After we have solved the equation, we have found
out that the rational equation given is TRUE. This
means that it has a real solution.
 But you must take note! If a given solution is not real
or ≠ and has a 0 on its denominator. Then it is called
an extraneous root

37. Awesome Words!
“Math is easy when it is Fun!
Don’t stress yourself and relax,
every solution has an answer”
—L.G. Writings

38. THANK YOU!
AND
BLESSED BE
GOD FOREVER!