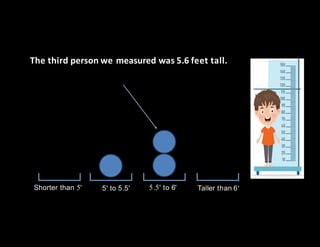
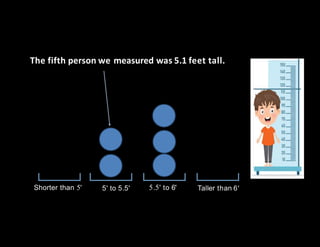
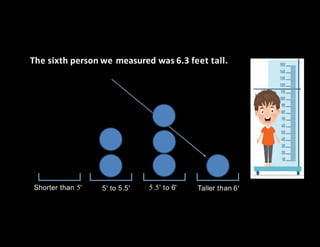
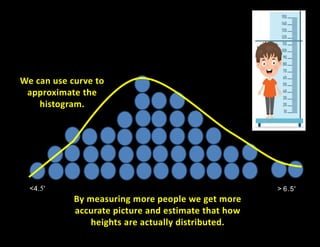
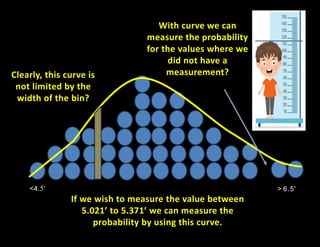
The document discusses random variables and probability distributions. It describes a scenario where X is the number of hours spent studying on a random school day. The probability that X takes on certain values (0, 1, 2, 3, or 4 hours) is given by a formula containing an unknown constant k. The questions ask to (1) find the value of k, and (2) calculate various probabilities related to the number of hours spent studying. The document then shifts to discussing histograms and probability distributions, using the example of measuring human heights and binning the results to visualize the distribution in a population. It describes how histograms can be approximated by curves to estimate probabilities across the full range of values.

1. Random Variables
and
Probability Distributions
Munir Ahmad

9. Question
Let X denote the number of hours you study during a randomly
selected school day. The probability that X can take the values x
has the following form where k is some unknown constant.
𝑃 𝑋 = 𝑥 =
0.1, 𝑖𝑓 𝑥 = 0
𝑘𝑥, 𝑖𝑓 𝑥 = 1 𝑜𝑟 2
𝑘 5 − 𝑥 , 𝑖𝑓 𝑥 = 3 𝑜𝑟 4
0, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
(a) Find the value of k.
(b) What is the probability that you study at least two hours?
Exactly two hours? At most two hours?

10. Part a

11. Part b

17. E

18. Imagine we measured the height of a lot of people.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

19. The first person we measured was 5.2 feet tall.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

20. The second person we measured was 5.8 feet tall.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

21. The third person we measured was 5.6 feet tall.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

22. The fourth person we measured was 5.9 feet tall.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

23. The fifth person we measured was 5.1 feet tall.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

24. The sixth person we measured was 6.3 feet tall.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'

25. So, we measure the
height of different
people and put the
measurements in
bins.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'
We call this setting as a Histogram.

26. People smaller
than 5’ are
relatively rare.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'
Most of the measurements
lie between 5’ and 6’.
People taller
than 6’ are
relatively rare.

27. People smaller
than 5’ are
relatively rare.
Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'
So, if we pick one measurement, it has
more chances to lie between 5’ and 6’.
People taller
than 6’ are
relatively rare.

28. Shorter than 5' 5' to 5.5' 5.5' to 6' Taller than 6'
So, if we pick one measurement, it has
more chances to lie between 5’ and 6’.

29. <4.5' 5.5' to 5.25'
With reduced bin size most measurements
lie between 5.25’ to 5.75’.
5.5 to 5.75' > 6.5'

30. <4.5'
By measuring more people we get more
accurate picture and estimate that how
heights are actually distributed.
> 6.5'

31. <4.5'
By measuring more people we get more
accurate picture and estimate that how
heights are actually distributed.
> 6.5'
We can use curve to
approximate the
histogram.

32. <4.5'
If we wish to measure the value between
5.021’ to 5.371’ we can measure the
probability by using this curve.
> 6.5'
With curve we can
measure the probability
for the values where we
did not have a
measurement?
Clearly, this curve is
not limited by the
width of the bin?

33. <4.5'
Also with very low measurements we can
still measure the curve.
> 6.5'
Curve and histogram
are both
distributions?
Their tallest part
show their best
spread of
measurements?

34. The End !!!