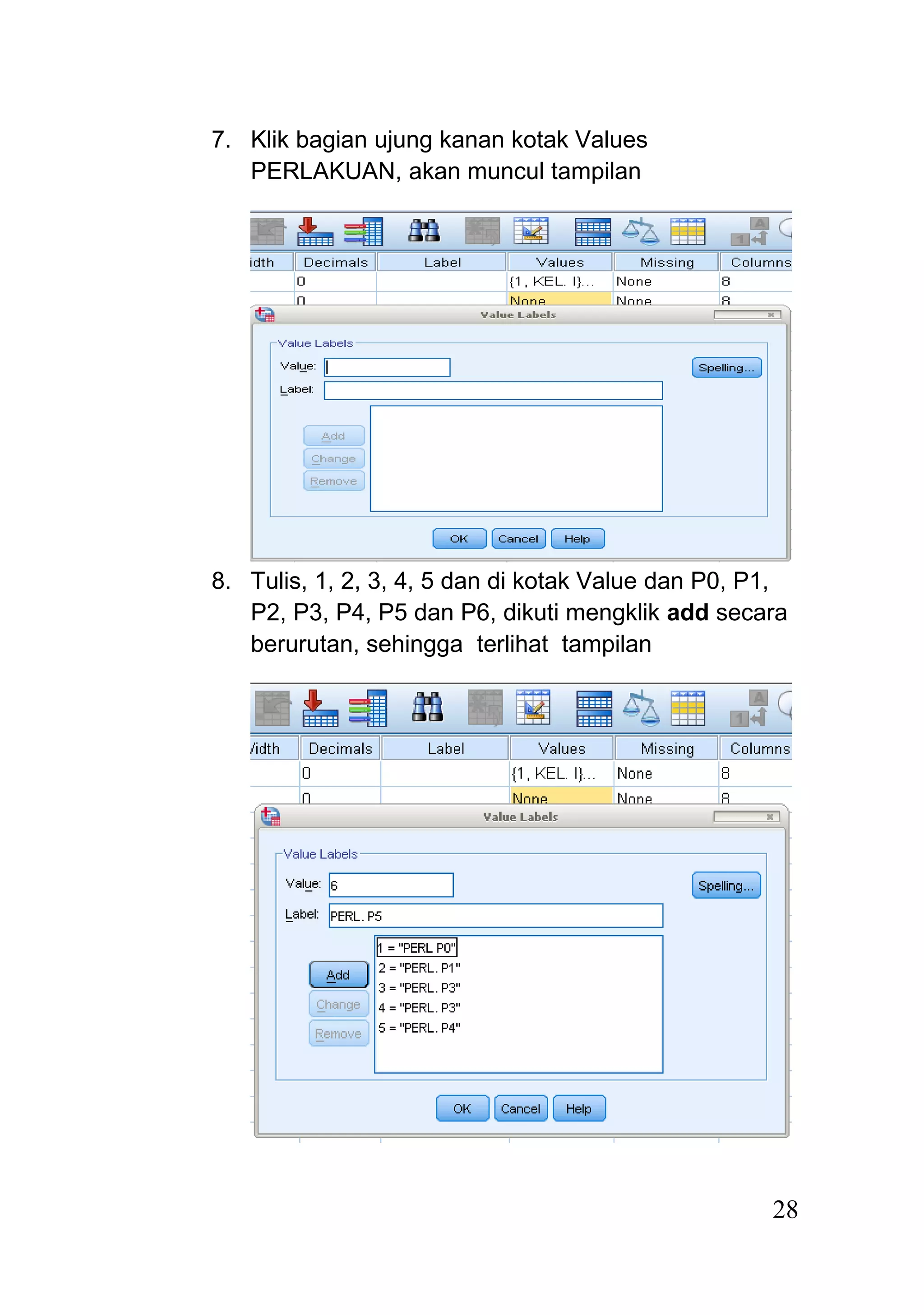
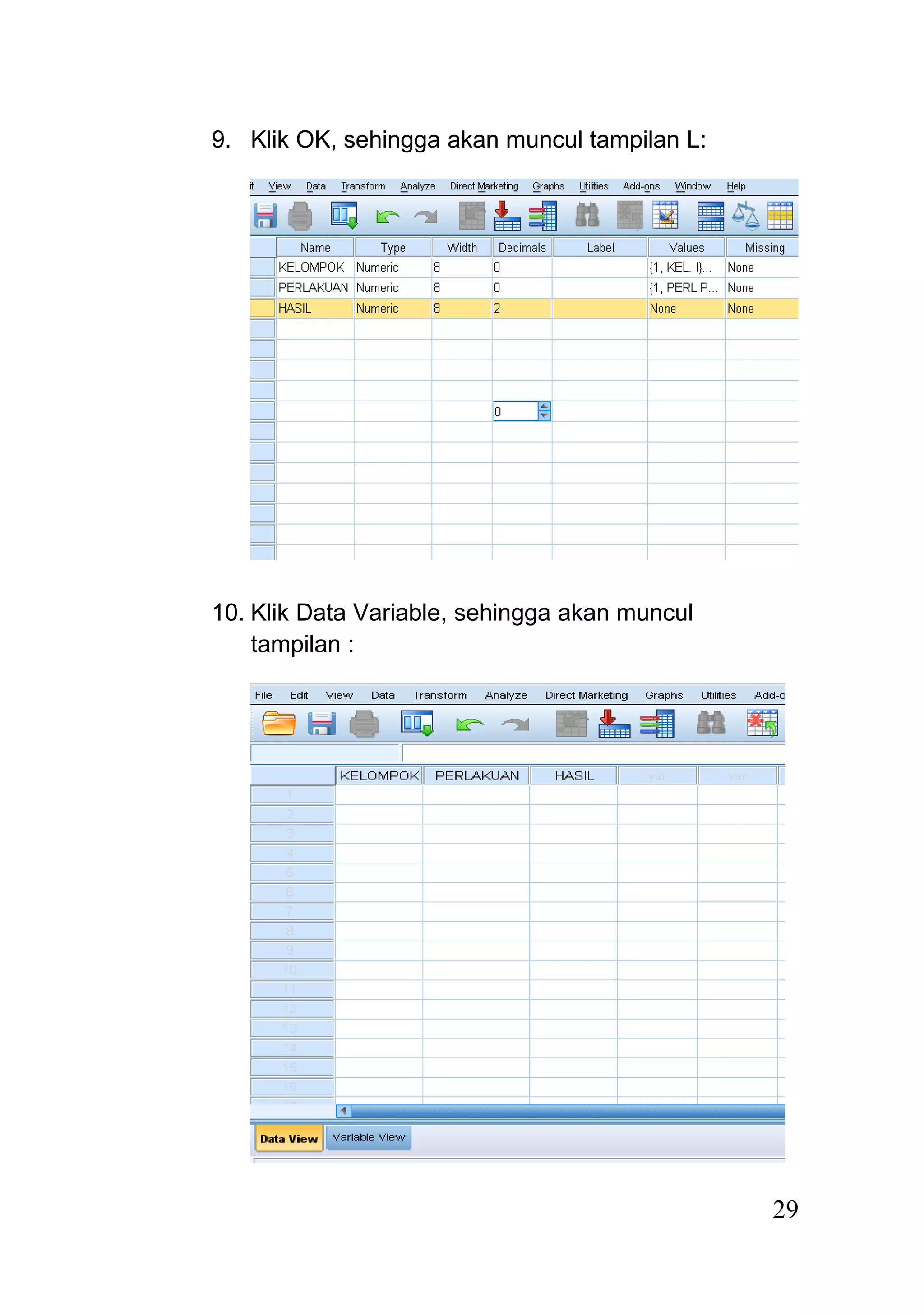
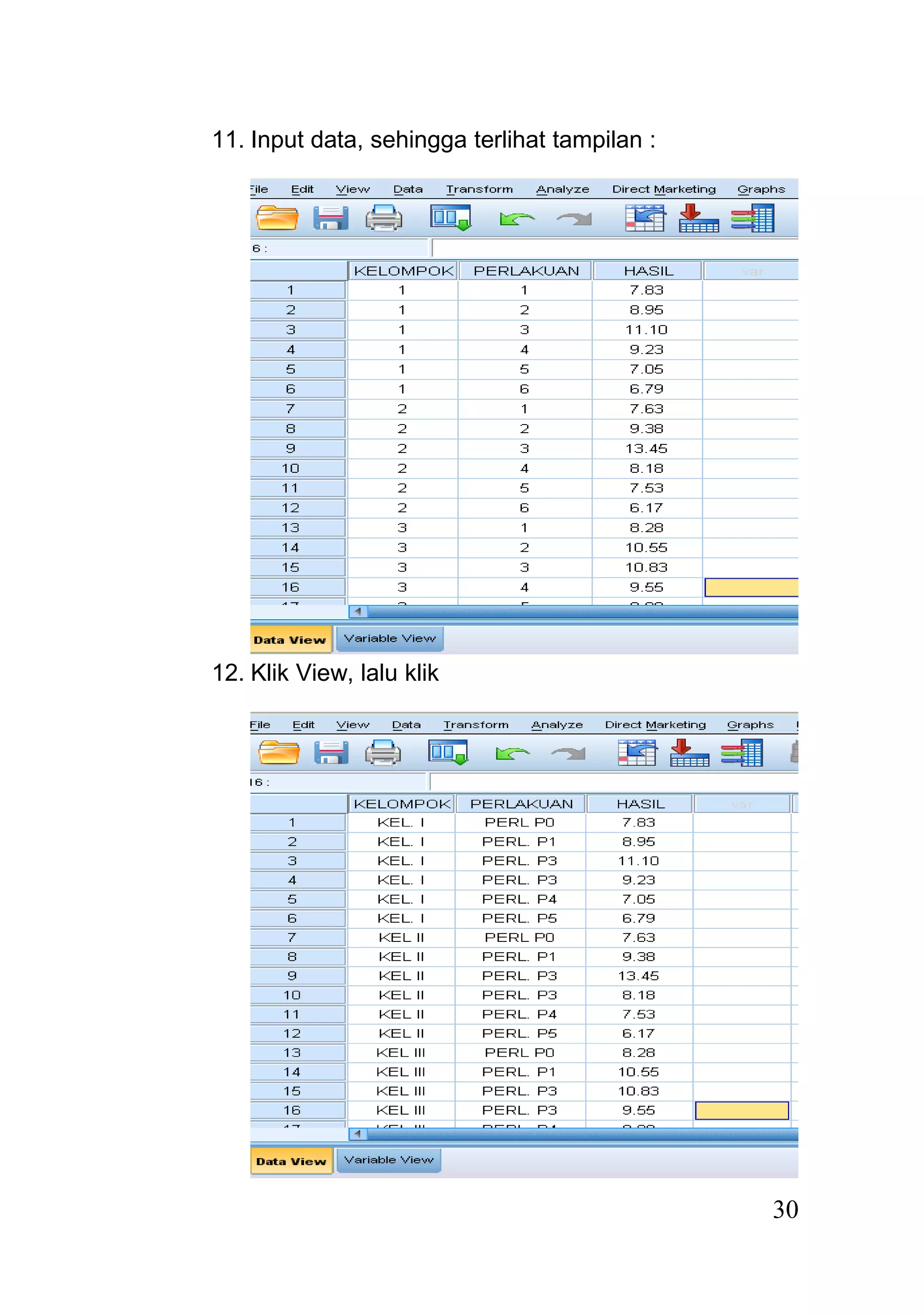
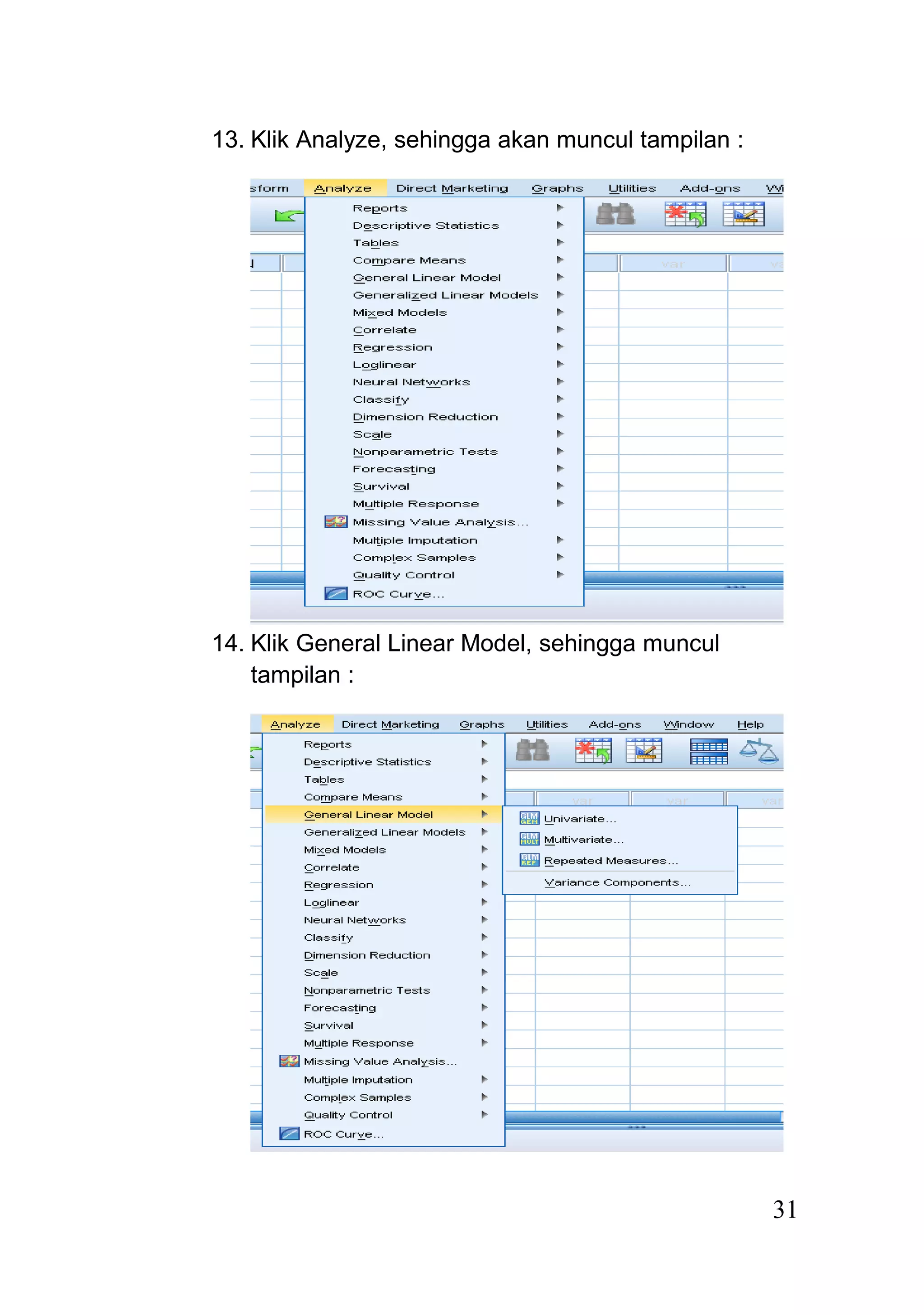
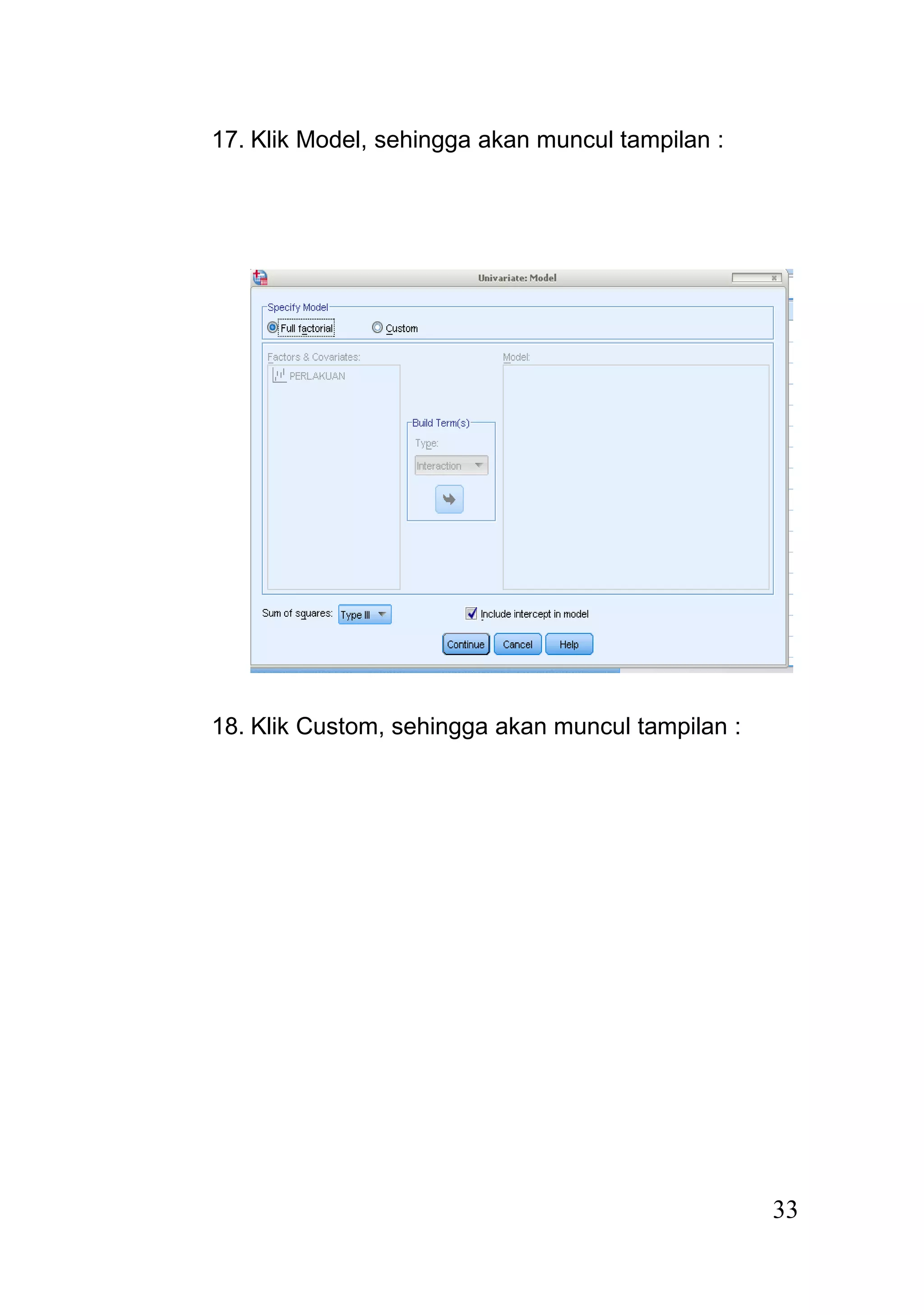
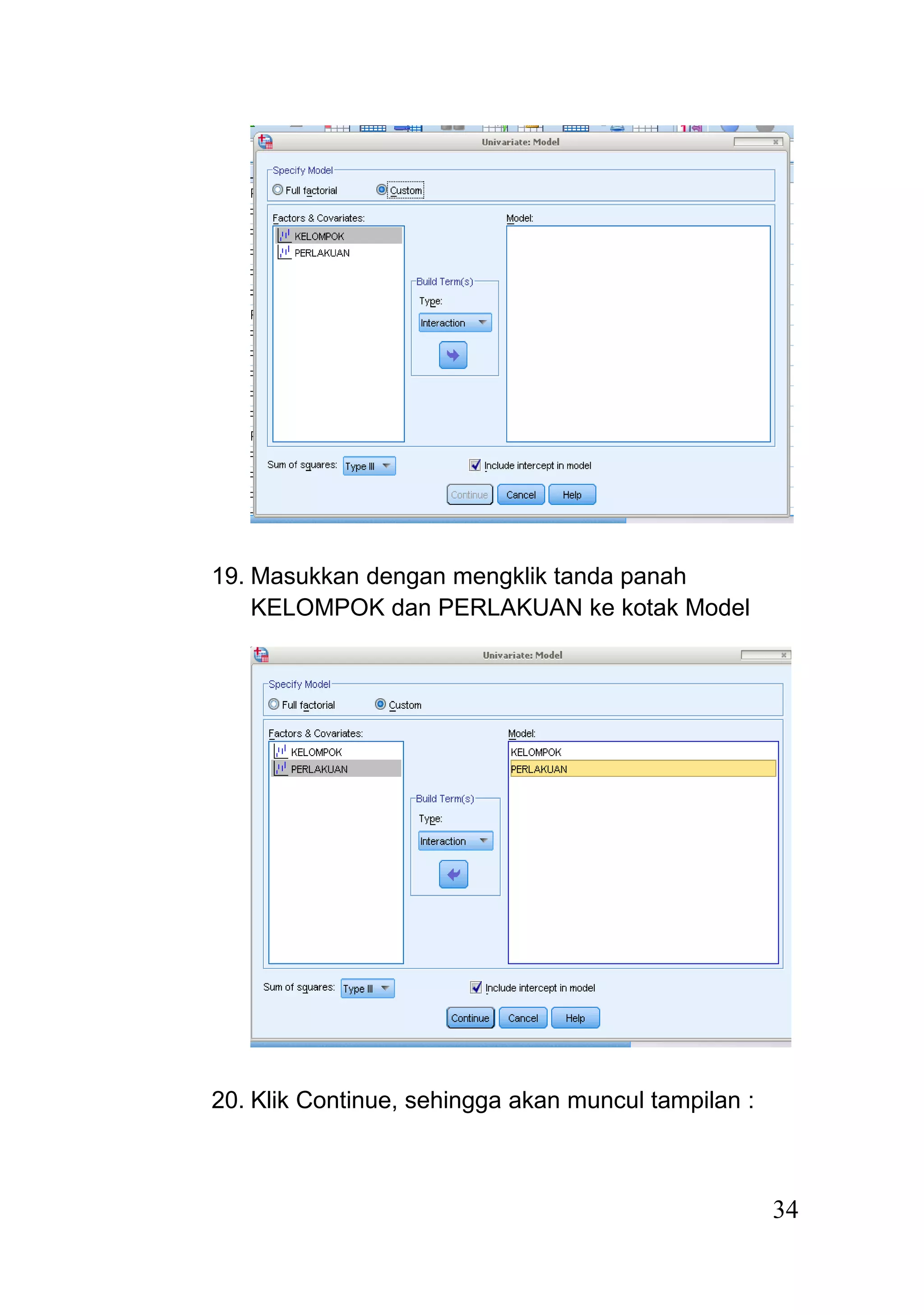
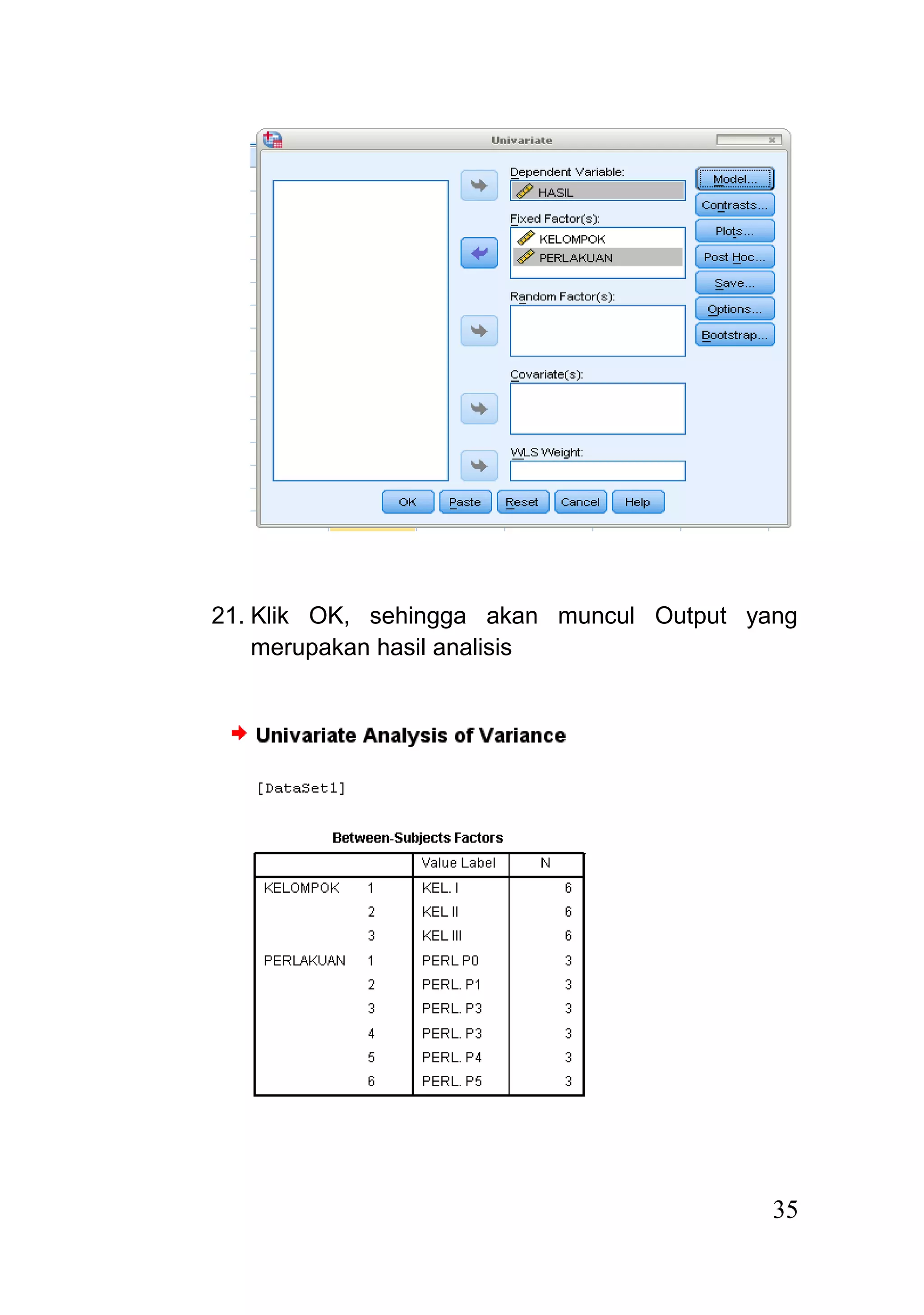
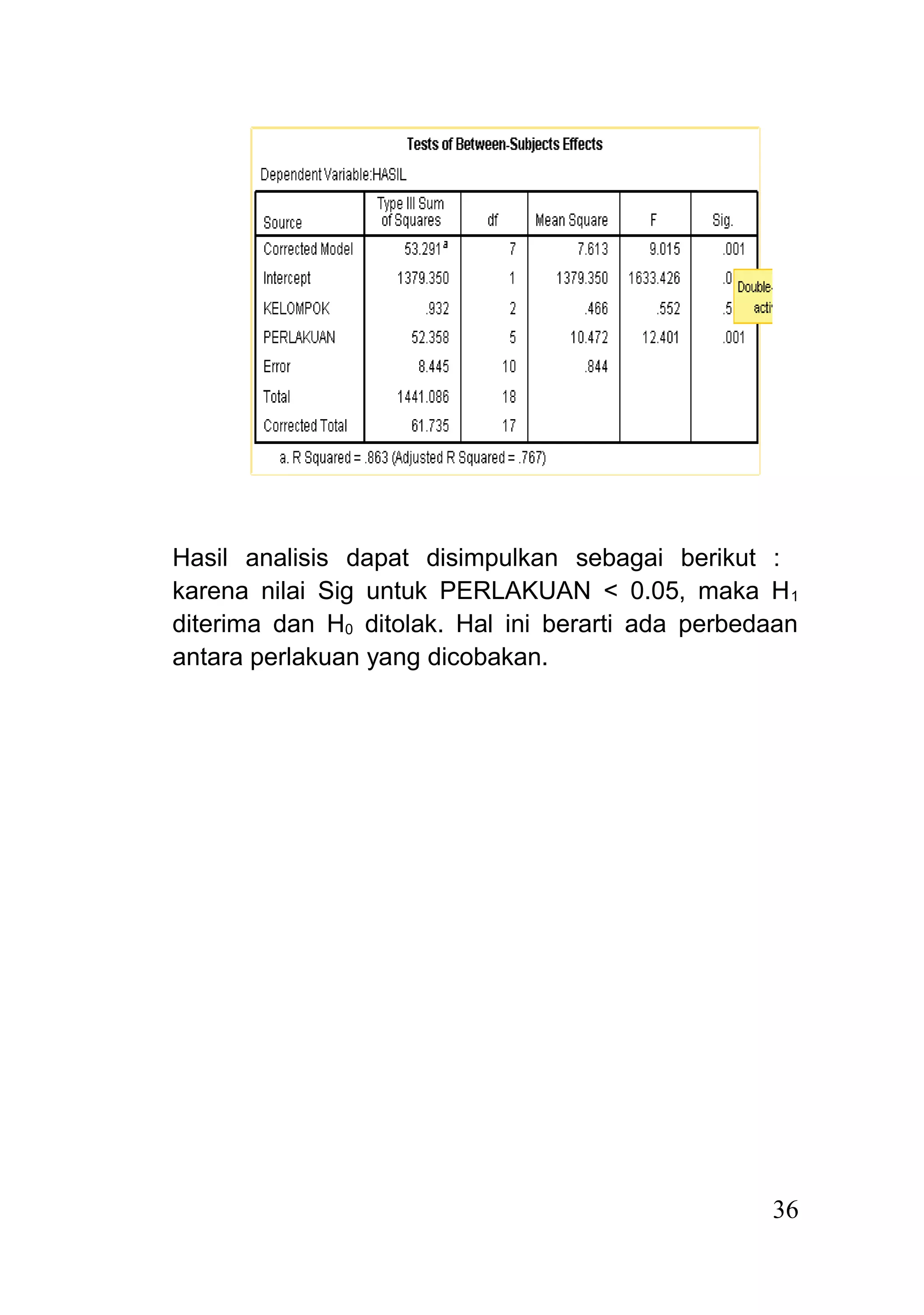
Dokumen ini menjelaskan rancangan acak kelompok (randomized block design) sebagai model percobaan yang digunakan untuk unit percobaan yang tidak homogen, dengan pengacakan perlakuan dilakukan dalam setiap kelompok. Analisis data dilakukan melalui langkah-langkah sistematis, termasuk pembuatan tabel analisis, uji hipotesis, dan dapat dilakukan menggunakan program seperti SPSS. Hasil dari analisis menunjukkan penerimaan atau penolakan hipotesis berdasarkan perbandingan nilai F hitung dan F tabel.

1. BAB III
RANCANGAN ACAK KELOMPOK
(Randomized Blok Design)
3.1 Teori dan Analisis Data Secara Manual
Rancangan Acak Kelompok atau randomized block
design merupakan salah satu model rancangan dalam
rancangan percobaan. Rancangan acak kelompok ini
digunakan bila unit percobaan tidak homogen, dimana
ketidak homogen ini diduga mengarah pada satu arah.
Rancangan ini disebut rancangan acak kelompok,
karena pengacakan perlakuan dilakukan pada setiap
kelompok. Rancangan ini dapat digunakan untuk
melakukan percobaan di lapangan atau di laboratorium
atau di rumah kaca.
Rancangan acak kelompok digunakan bila faktor yang
akan diteliti satu faktor atau lebih dari satu faktor. Pada
percobaan dengan menggunakan rancangan faktorial
(lebih dari satu faktor) rancangan acak kelompok menjadi
rancangan lingkungan.
Model linier yang tepat untuk rancangan acak
kelompok adalah:
Yij(t) = µ + Kj + P(t) + εi(t)
dimana:
i = 1, 2, ...n; dan t = 1, 2, ...n
19

2. Yi(t) = nilai pengamatan pada baris
ke-i, kolom ke-j yang
mendapat perlakuan ke-t.
µ = nilai rata-rata umum
Ki = pengaruh kelompok ke-i
P(t) = pengaruh perlakuan ke-t
ei(t) = pengaruh galat pada kelompok
ke-i, yang memperoleh
perlakuan ke-t
Rancangan acak kelompok berguna untuk
melaksanakan percobaan bila unit percobaan tidak
homogen.
Pelaksanaan percobaan dengan menggunakan
rancangan acak kelompok dilaksanakan dengan langkah-
langkah sebagai berikut :
Pengacakan, yaitu penempatan perlakuan pada unit
percobaan secara harus dilakukan secara acak.
1. Tentukan jumlah perlakukan dan jumlah
kelompok
2. Tentukan lokasi percobaan
3. Buat rancangan denah percobaan berdasarkan
jumlah perlakuan dan jumlah kelompok
20

3. 4. Lakukan pengacakan perlakuan pada setiap
kelompok dan buat denah percobaan.
5. Berdasarkan denah percobaan, laksanakan
percobaan di lapang atau di laboratorium atau di
rumah kaca
Analisis data dilakukan dengan langkah-langkah
sebagai berikut :
1. Lakukan pengamatan sesuai dengan rencana
2. Buat tabel analisis data
21

4. Tabel 3.1. Tabel Hasil Pengamatan
3. Lakukan analisis data (berdasarkan data pada
Tabel 3.1)
Tabel 3. 2. Cara Analisis Data
22

5. 4. Buat tabel sidik ragam berdasarkan hasil analisis
data
Tabel 3 Sidik Ragam
5. Berdasarkan tabel sidik ragam, lakukan uji
hipotesis dengan membandingkan F. Hitung
dengan F. Tabel
Kaidah keputusan yang harus diambil adalah
sebagai berikut:
a. Jika F. Hitung > F. Tabel pada taraf 1% (α =
0,01), perbedaan diantara nilai tengah baris
atau kolom atau perlakuan (atau pengaruh
baris atau kolom atau perlakuan) dikatakan
berbeda sangat nyata (pada hasil F. Hitung
ditandai dengan dua tanda **).
b. Jika F. Hitung > F. Tabel pada taraf 5% (α =
0,05) tetapi lebih kecil daripada F. Tabel
pada taraf 1%, perbedaan diantara nilai
23

6. tengah baris atau kolom atau perlakuan
dikatakan berbeda nyata (pada hasil F.
Hitung ditandai dengan satu tanda *).
c. Jika F. Hitung ≤ F. Tabel pada taraf 5% (α =
0,05), perbedaan diantara nilai tengah baris
atau kolom atau perlakuan dikatakan tidak
nyata (pada hasil F. Hitung ditandai dengan
tn)
6. Bila H1 diterima, lakukan uji lanjutan
7. Buat kesimpulan
Analisis data juga dapat dilakukan dengan
menggunakan program Excel atau Program SPSS
IRRISTAT dan lain-lain. Cara analisisnya dengan
menggunakan program SPSS akan dijelaskan pada
sub bab 3.1
3.2 Analisis dengan Menggunakan Program SPSS
Data yang akan dianalisis, dapat dilihat pada tabel di
bawah ini
24

7. 1. Buka Program SPSS, sehingga akan muncul
tampilan :
2. Klik saja Cancel, sehingga akan muncul tampilan :
25

8. 3. Klik Variable View, sehingga akan muncul
tampilan :
4. Tulis nama variable, KELOMPOK dan
PERLAKUAN seperti tampilan :
26

9. 5. Klik bagian ujung kanan kotak Values KELOMPOK,
akan muncul tampilan
6. Tulis, 1, 2, 3 di kotak Value dan Kel I, Kel II dan Kel
III, dikuti mengklik add secara berurutan, sehingga
terlihat tampilan :
27

10. 7. Klik bagian ujung kanan kotak Values
PERLAKUAN, akan muncul tampilan
8. Tulis, 1, 2, 3, 4, 5 dan di kotak Value dan P0, P1,
P2, P3, P4, P5 dan P6, dikuti mengklik add secara
berurutan, sehingga terlihat tampilan
28

11. 9. Klik OK, sehingga akan muncul tampilan L:
10. Klik Data Variable, sehingga akan muncul
tampilan :
29

12. 11. Input data, sehingga terlihat tampilan :
12. Klik View, lalu klik
30

13. 13. Klik Analyze, sehingga akan muncul tampilan :
14. Klik General Linear Model, sehingga muncul
tampilan :
31

14. 15. Klik Univariate, sehingga muncul tampilan :
16. Masukkan dengan mengklik tanda panah,
KELOMPOK dan PERLAKUAN ke kotak Fixed
Factor(s) dan HASIL ke kotak Dependent variable,
sehingga terlihat seperti tampilan :
32

15. 17. Klik Model, sehingga akan muncul tampilan :
18. Klik Custom, sehingga akan muncul tampilan :
33

16. 19. Masukkan dengan mengklik tanda panah
KELOMPOK dan PERLAKUAN ke kotak Model
20. Klik Continue, sehingga akan muncul tampilan :
34

17. 21. Klik OK, sehingga akan muncul Output yang
merupakan hasil analisis
35

18. Hasil analisis dapat disimpulkan sebagai berikut :
karena nilai Sig untuk PERLAKUAN < 0.05, maka H1
diterima dan H0 ditolak. Hal ini berarti ada perbedaan
antara perlakuan yang dicobakan.
36