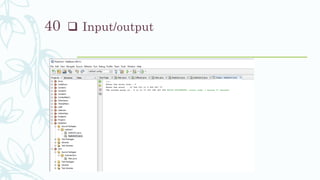
This document presents a summary of Radix Sort by MD. Tanvir Ahammed Hridoy. It begins with definitions of Radix Sort and discusses its history, properties, algorithm, complexity, an example, Java code, advantages and disadvantages. Radix Sort is a non-comparative sorting algorithm that sorts integers by grouping keys based on individual digit values and their significant positions. It has a linear runtime of O(n) and requires a minimum amount of space and data movement. Counting Sort is often used to sort each digit. While fast for small keys, Radix Sort only works for numbers with a fixed number of digits.

1. NAME: MD. Tanvir Ahammed Hridoy
ID: B-180305020
Presentation Topic : Radix Sort
Course Code: CSE 2209
1

2. 2
SPECIAL THANKS
LINTA ISLAM
LECTURER
DEPARTMENT OF COMPUTER SCIENCE & ENGINEERING
FACULTY OF SCIENCE
JAGANNATH UNIVERSITY,DHAKA

3. Contents
– Definition of Radix Sort
– History
– Properties
– Algorithm
– Complexity
– Example
– Java Code
– Advantages and Disadvantages
– Reference
3

4. RADIX SORT
 Definition: In Computer Science Radix Sort is a non – comparative integer sorting
algorithm that sort data with integer keys by grouping keys by the individual digits which
share same significant position and value. Radix Means the base of a system of
numeration.
 Example:
• The decimal number system that we use every day has 10 digits {0,1,2,3,4,5,6,7,8,9}
and so the radix is 10.
4

5. History
 Radix sort dates back as far as 1887 to the work of Herman
Hollerith on tabulating machines . Radix sorting algorithms came into common
use as a way to sort punched cards as early as 1923.
 The first memory-efficient computer algorithm was developed in 1954
at MIT by Harold H. Seward .Computerized radix sorts had previously been
dismissed as impractical because of the perceived need for variable allocation
of buckets of unknown size.
5

6. Properties
 Purpose of Use:
1. It requires the absolute minimum amount of space.
2. minimum amount of data movement.
3. Most amazing of all, it does no comparisons like(Quick Sort
,Insertion sort , merge Sort etc.)
 CLASSIFIACATION:
1. Least Significant Digit (LSD) radix sorts
2. Most Significant Digit (MSD) radix sorts
6

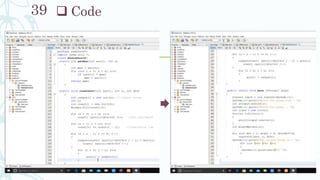
7. Algorithm
 RadixSort(array,size)
Step 1: take array[size]
Step 2: Get max from the array
m=GetMax(array,size)
Step 3: do counting sort for every digit
for div=1 to m/div>0 where div=div*10
countingSort(arr,size,div)
 GetMax( array,size)
Step 1 : max=array[0]
Step2 : for i=1 to i<size
if arr[i]>max
max=arr[i]
Step 3: return max
7
 CountingSort(array,size,div)
Step 1: create output[size]
Step 2: Take range // number of unique elements
Step 3: for i=0 to i<range
count[i] = 0
Step 4: for i=0 to i<size
count[(array[i]/div)%10]++
Step 5: for i=1 to i<range
count[i]= count[i]+count[i-1]
Step 6: for i=size-1 to i>=0
output[count[(array[i]/div)%10]-1]= array[i]
count[ (arr[i]/div)%10 ]--;
Step 7: for i=0 to i<size
array[i]=output[i]
100 50 72 24 85
Example

8. Complexity
 Each pass over n digit numbers and k base keys then take time
O(n+k)(assuming counting sort is used for each pass.)
 There are d is the passes , so total time for radix sort is O(d(n+k)) .
 When d is constant and total run time =O(n).
 The algorithm runes in linear time when n and k are the same size magnitude
then it will better than O(nlog n)of comparative sort algorithm.
Worst Case: O(n)
Best Case: O(n)
Average Case: O(n)
8

9. 9

10. 10

11. 11

12. 12

13. 13

14. 14

15. 15

16. 16

17. 17

18. 18

19. 19
N.B: It use the concept of first in first out(fifo).

20. 20

21. 21

22. 22

23. 23

24. 24

25. 25

26. 26

27. 27

28. 28
N.B: It use the concept of first in first out(fifo).

29. 29

30. 30

31. 31

32. 32

33. 33

34. 34

35. 35

36. 36

37. 37
N.B: It use the concept of first in first out(fifo).

38. 38

39.  Code
39

40.  Input/output
40

41.  Conclusion
 Advantage:
1. Radix sort is stable and fast
2.Somtimes , it would be faster than quicksort or heapsort.
3. It is good on small keys .
 Disadvantages:
1. Radix sort only works when sorting numbers with a fixed number of
digits. It won’t work for arbitrarily-large numbers.
2. It takes more space compared to Quicksort which is inplace sorting.
41

42.  References
– Google
– YouTube
– Wikipedia
– www.geeksforgeeks.org
42

43. 43
Thanks everyone to cooperate with me.
Any Query?