The document describes the merge sort algorithm. It works by dividing an input array into two halves, recursively sorting the halves, and then merging the sorted halves back together. The algorithm has a runtime of Θ(nlog(n)) in all cases. Pseudocode and implementations in C++, Java, and Python are provided to illustrate how merge sort divides, sorts, and merges the array halves.

1. Algorithms
Merge Sort
Abdelrahman M. Saleh

2. List of contents
● Introduction
● Example w/ illustrating figures
● Algorithm
● implementation (Java, C++, Python)
● Performance Runtime
○ Best, Average and worst cases.
● Execution
● Other Notes

3. Introduction
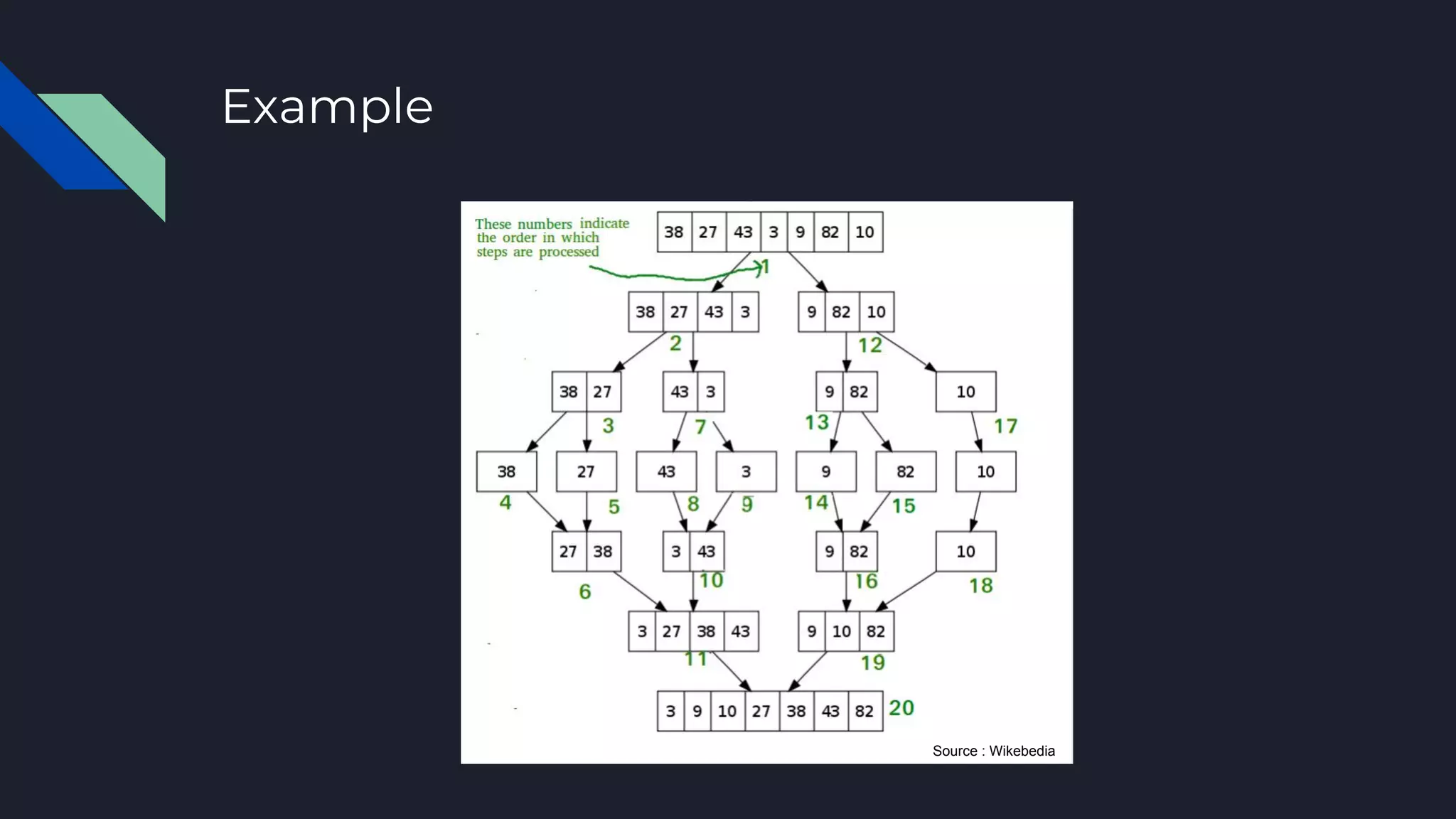
● Divide and Conquer algorithm. It divides input array in two halves, calls itself for the
two halves and then merges the two sorted halves.
● The merge() function is used for merging two halves The merge(a, l, m, r) is key process
that assumes that a[l..m] and a[m+1..r] are sorted and merges the two sorted sub-arrays
into one .

4. Example
Source : Wikebedia

5. Algorithm .
➔ Array name “arr” , left-most element “l”, right-most element “r”
● If r is bigger than l
○ Find the middle point to divide the array into two halves :
■ middle m = (l+r)/2
○ Call mergeSort for first half :
■ Call mergeSort(arr, l, m)
○ Call mergeSort for second half :
■ Call mergeSort(arr, m+1, r)
○ Merge the two halves sorted in step 2 and 3 :
■ Call merge(arr, l, m, r)

6. Implementation .

7. C++
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
//Same as (l+r)/2, but avoids overflow for large l and r .
int m = l+(r-l)/2;
// Sort first and second halves
mergeSort(arr, l, m);
mergeSort(arr, m+1, r);
merge(arr, l, m, r);
}
}

8. C++
Continue ...
void merge(int arr[], int l, int m, int r)
{
int i = 0, j = 0, k = 1 ;
int n1 = m - l + 1;
int n2 = r - m;
int L[n1], R[n2]; /* create temp arrays */
/* Copy data to temp arrays L[] and R[] */
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1+ j];
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

9. C++
Continue ...
/* Merge the temp arrays back into arr[l..r]*/
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i]; i++;
}
else
{
arr[k] = R[j]; j++;
}
k++;
}
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

10. C++
Continue ...
/* Copy the remaining elements of L[], if there are any */
while (i < n1)
{
arr[k] = L[i]; i++; k++;
}
/* Copy the remaining elements of R[], if there are any */
while (j < n2)
{
arr[k] = R[j]; j++; k++;
}
}
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

11. JAVA
void mergeSort(int arr[], int l, int r)
{
if (l < r)
{
// Find the middle point
int m = (l+r)/2;
// Sort first and second halves
mergeSort(arr, l, m);
mergeSort(arr , m+1, r);
merge(arr, l, m, r);
}
}

12. JAVA
Continue ...
/* Merge the temp arrays back into arr[l..r]*/
void merge(int arr[], int l, int m, int r)
{
int n1 = m - l + 1;
int n2 = r - m;
int L[] = new int [n1]; /* Create temp arrays */
int R[] = new int [n2];
/*Copy data to temp arrays*/
for (int i=0; i<n1; ++i)
L[i] = arr[l + i];
for (int j=0; j<n2; ++j)
R[j] = arr[m + 1+ j];
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

13. JAVA
Continue ...
int i = 0, j = 0, int k = l ; // Initial indexes of first, second and merged subarrays relatively .
while (i < n1 && j < n2)
{
if (L[i] <= R[j])
{
arr[k] = L[i]; i++;
}else{
arr[k] = R[j]; j++;
}
k++;
}
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

14. JAVA
Continue ...
/* Copy the remaining elements of L[], if there are any */
while (i < n1)
{
arr[k] = L[i]; i++; k++;
}
/* Copy the remaining elements of R[], if there are any */
while (j < n2)
{
arr[k] = R[j]; j++; k++;
}
}
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

15. Python .
def mergeSort(arr, l, r):
if l < r :
m = (l+(r-1))/2 #Same as (l+r)/2, but avoids overflow for large l and r
#Sort first and second halves
mergeSort(arr, l, m)
mergeSort(arr, m+1, r)
merge(arr, l, m, r)

16. Python
Continue ...
def merge(arr, l, m, r):
n1 = m - l - 1
n2 = r - m
L = [0] * (n1) #create temp arrays
R = [0] * (n2)
#copy data to temp arrays
for i in range (0, n1):
L[i] = arr(l + i)
for j in range (0, n2):
R[j] = arr(m + 1 + j)
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

17. Python
Continue ...
i = 0
j = 0
k = l
while i < n1 and j < n2:
if L[i] <= R[j]:
arr[k] = L[i]
i += 1
else:
arr[k] = R[i]
j += 1
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

18. Python .
#Copy the remaining elements of L[], if there are any
while i < n1:
arr[k] = L[i]
i += 1
k += 11
#Copy the remaining elements of R[], if there are any
while j < n2:
arr[k] = R[j]
j += 1
k += 1
// Merges two subarrays of arr[] : arr[l..m], arr[m+1..r]

19. Performance Runtime
● Time complexity Θ(nlog(n)) .
● In merge sort Best, Average and Worst cases are the same “Θ(nlog(n))” as it always
divides the array in two halves and take linear time to merge two halves.

20. Execution .
Input array : [4, 6, 3, 2, 1, 9, 7]
Output Array: [1, 2, 3, 4, 6, 7, 9]

21. Other Notes .
● Algorithmic Paradigm: Divide Approach
● Sorting In Place: No
● Stable: Yes
● Online: Yes