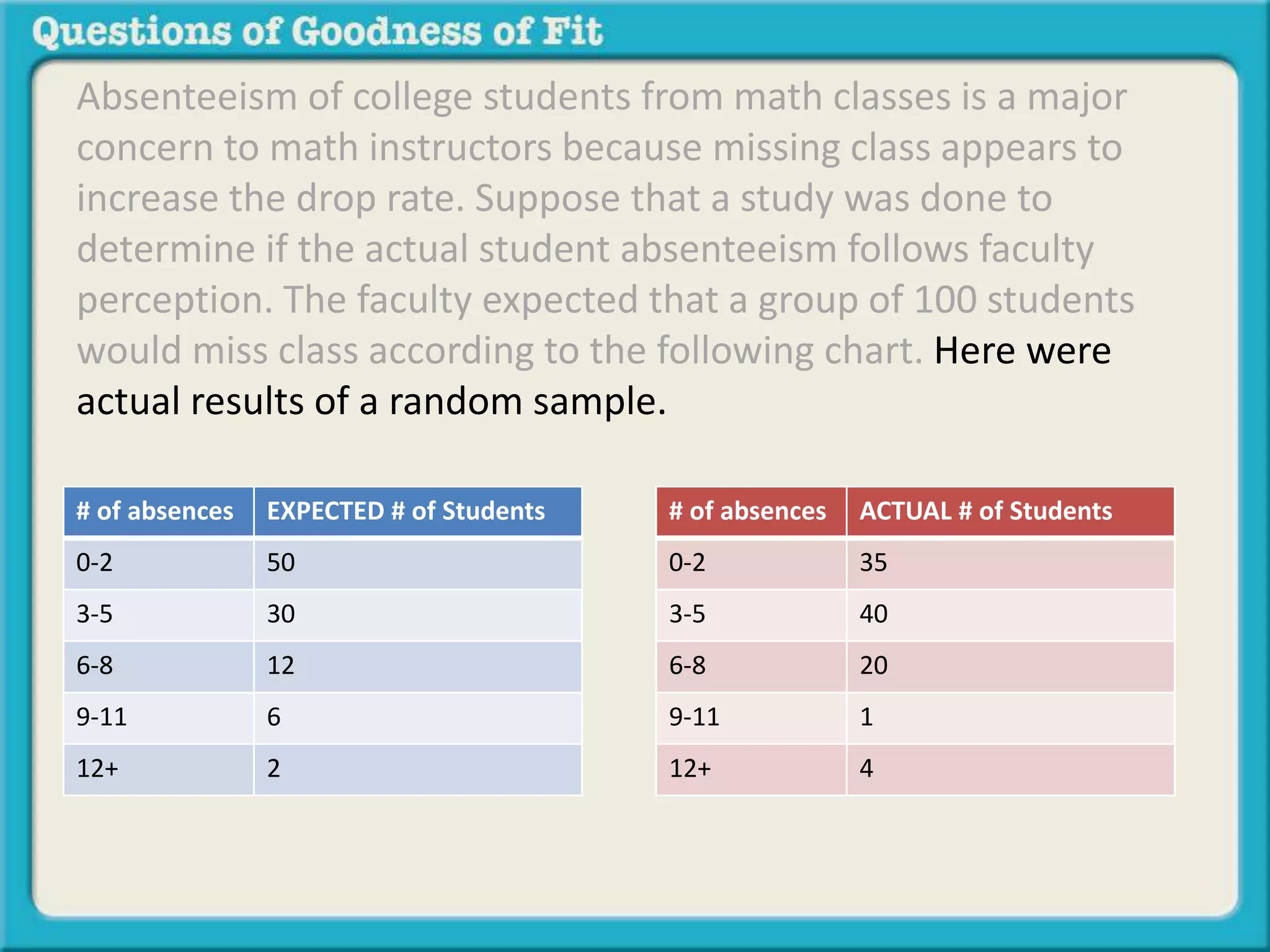
This document discusses goodness of fit, which determines how close an observed pattern fits a hypothesized pattern. It provides examples comparing hypothesized and actual counts or percentages to determine if they are statistically significantly different. If comparing counts, a goodness of fit test is used, while a difference test is used for percentages. The document explains this using examples of testing the distribution of M&M colors and rates of student absenteeism.

1. Questions of Goodness of Fit

2. Is the problem you are working on a question of
Goodness of Fit?

3. Is the problem you are working on a question of
Goodness of Fit?

4. Questions of Goodness of Fit have become increasingly
important in modern statistics.

5. Goodness of fit is a method used to determine how close
a hypothesized pattern fits an observed pattern.

6. Goodness of fit is a method used to determine how close
a hypothesized pattern fits an observed pattern.
Hypothesized Pattern-the
way you think
things are.

7. Goodness of fit is a method used to determine how close
a hypothesized pattern fits an observed pattern.
fits
Hypothesized Pattern-the
way you think
things are.

8. Goodness of fit is a method used to determine how close
a hypothesized pattern fits an observed pattern.
Observed Pattern –
the way things
actually are.
Hypothesized Pattern-the
way you think
things are.
fits

9. For example, let’s say we hypothesize that there are an
equal number of females as there are males in the town
of Solvang, California.

10. So, in a sample of 200 Solvangans we would hypothesize
that 100 would be female.

11. So, in a sample of 200 Solvangans we would hypothesize
that 100 would be female.
The hypothesized
number
of females in a
sample of 200 is
100

12. So, in a sample of 200 Solvangans we would hypothesize
that 100 would be female.
The hypothesized
number
of females in a
sample of 200 is
100
That is because we assume
that an equal number will be
males and an equal number
will be females

13. We then take a sample of 200 and find that there are
actually 84.

14. Once again, our hypothesized number of females from a
sample of 200 is 100.

15. Once again, our hypothesized number of females from a
sample of 200 is 100.
The hypothesized
number
of females in a
sample of 200 is
100

16. But, our actual number of females from a sample of 100
is 84.

17. Is the difference between 100 and 84 statistically
significant?

18. Is the difference between 100 and 84 statistically
significant?
Note - Even though we are using
the word difference here, in this
case we are referring to how well
the data FITS the hypothesis.

19. Is the difference between 100 and 84 statistically
significant?
The HYPOTHESIZED
number
of females in a
sample of 200 is
100

20. Is the difference between 100 and 84 statistically
significant?
The ACTUAL
number
of females in a
sample of 200 is
84
The HYPOTHESIZED
number
of females in a
sample of 200 is
100

21. Is the difference between 100 and 84 statistically
significant?
The ACTUAL
number
of females in a
sample of 200 is
84 16
The HYPOTHESIZED
number
of females in a
sample of 200 is
100

22. Is the difference between 100 and 84 statistically
significant?
The ACTUAL
number
of females in a
sample of 200 is
84 16
The HYPOTHESIZED
number
of females in a
sample of 200 is
100

23. If it is significantly different, then we may need to collect
a new sample that is more representative of the
hypothesized population.

24. If it is significantly different, then we may need to collect
a new sample that is more representative of the
hypothesized population.

25. Here is an equation that we will use as a guide
to identify goodness of fit questions.

26. Here is an equation that we will use as a guide
to identify goodness of fit questions.
Hypothesized
Number
fit the
Actual
Number
Does the ?

27. Examples of Goodness of Fit Tests

28. Example #1

29. Consider a standard package of milk chocolate M&Ms.

30. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown.

31. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally?

32. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.

33. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.
Are these differences statistically significant?

34. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.
Are these differences statistically significant?
Hypothesized
Number
fit the
Actual
Number
Does the ?

35. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.
Are these differences statistically significant?
Hypothesized
Number
fit the
Actual
Number
Does the ?

36. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.
Are these differences statistically significant?
fit the
Actual
Number
Does the
Hypothesized
Number =
4 red, 4 orange
4 yellow, 4 green
4 blue, 4 brown
?

37. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.
Are these differences statistically significant?
fit the
Actual
Number
Does the
Hypothesized
Number =
4 red, 4 orange
4 yellow, 4 green
4 blue, 4 brown
?

38. Consider a standard package of milk chocolate M&Ms.
There are six different colors: red, orange, yellow,
green, blue and brown. Suppose that we are curious
about the distribution of these colors and ask, do all six
colors occur equally? You collect 24 M&Ms with 4 reds,
4 oranges, 3 yellows, 5 greens, 2 blues, & 6 browns.
Are these differences statistically significant?
Hypothesized
Number =
4 red, 4 orange
4 yellow, 4 green
4 blue, 4 brown
Does the fit the
Actual
Number =
4 red, 4 orange
3 yellow, 5 green
2 blue, 6 brown
?

39. Example #2

40. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate.

41. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception.

42. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart.

43. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart.
# of absences EXPECTED # of Students
0-2 50
3-5 30
6-8 12
9-11 6
12+ 2

44. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample.
# of absences EXPECTED # of Students
0-2 50
3-5 30
6-8 12
9-11 6
12+ 2

45. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample.
# of absences EXPECTED # of Students
0-2 50
3-5 30
6-8 12
9-11 6
12+ 2
# of absences ACTUAL # of Students
0-2 35
3-5 40
6-8 20
9-11 1
12+ 4

46. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample. Did the faculty perception fit
the reality?
Hypothesized
Number
fit the
Actual
Number
Does the ?

47. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample. Did the faculty perception fit
the reality?
Hypothesized
Number
fit the
Actual
Number
Does the ?

48. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample. Did the faculty perception fit
the reality?
Faculty
Perceptions
of Student
Absenteeism
fit the
Actual
Number
Does the ?

49. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample. Did the faculty perception fit
the reality?
Faculty
Perceptions
of Student
Absenteeism
fit the
Actual
Number
Does the ?

50. Absenteeism of college students from math classes is a major
concern to math instructors because missing class appears to
increase the drop rate. Suppose that a study was done to
determine if the actual student absenteeism follows faculty
perception. The faculty expected that a group of 100 students
would miss class according to the following chart. Here were
actual results of a random sample. Did the faculty perception fit
the reality?
Actual
Student
Absenteeism
Faculty
Perceptions
of Student
Absenteeism
Does the fit the ?

51. An exception to the rule

52. An exception to the rule
As was just shown, if you are comparing an
observed count with a hypothesized count,
then you will use goodness of fit statistical
methods.

53. An exception to the rule
As was just shown, if you are comparing an
observed count with a hypothesized count,
then you will use goodness of fit statistical
methods.
Hypothesized
Count = 100
Actual
Count = 84

54. An exception to the rule
As was just shown, if you are comparing an
observed count with a hypothesized count,
then you will use goodness of fit statistical
methods.
Hypothesized
Count = 100
Actual
Count = 84

55. An exception to the rule
However,

56. An exception to the rule
However, if you are comparing a hypothesized
proportion (5 out of 10) or percentage (50%)

57. An exception to the rule
However, if you are comparing a hypothesized
proportion (5 out of 10) or percentage (50%)
with an actual proportion or percentage, then
you will use a “Difference” method.

58. An exception to the rule
However, if you are comparing a hypothesized
proportion (5 out of 10) or percentage (50%)
with an actual proportion or percentage, then
you will use a “Difference” method.
Hypothesized
Percentage =
50%
Actual
Percentage =
42%

59. An exception to the rule
However, if you are comparing a hypothesized
proportion (5 out of 10) or percentage (50%)
with an actual proportion or percentage, then
you will use a “Difference” method.
Hypothesized
Percentage =
50%
Actual
Percentage =
42%

60. Here are the two classifications with their
equations:

61. Question of Goodness of Fit:

62. Question of Goodness of Fit:
Hypothesized
Number
Actual
Number
Does the fit the ?

63. Question of Goodness of Fit:
Hypothesized
Number
Question of Difference:
Actual
Number
Does the fit the ?

64. Question of Goodness of Fit:
Hypothesized
Does the fit the ?
Number
Question of Difference:
Actual
Number
Hypothesized
Percentage or
Proportion
differ
Actual
Percentage or
Proportion
Does the
?

65. Let’s see an example:

66. You have been asked to determine if a sample is
representative of the general population in
terms of gender.

67. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample of 500 should have 250 females.

68. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample of 500 should have 250 females.
However, in your sample there are 325 females.

69. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample of 500 should have 250 females.
However, in your sample there are 325 females.
How well does your sample of 325 fit this
hypothesized expectation statistically?

70. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample of 500 should have 250 females.
However, in your sample there are 325 females.
How well does your sample of 325 fit this
hypothesized expectation statistically?
Since this question is dealing with number
counts, it will be classified as a
Goodness of Fit Question

71. Now let’s see the same question but as a
“difference” question.

72. You have been asked to determine if a sample is
representative of the general population in
terms of gender.

73. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample should have 50% females.

74. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample should have 50% females. However,
in your sample there are 65% females.

75. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample should have 50% females. However,
in your sample there are 65% females. How
much does your sample of 65% differ from the
hypothesized expectation of 50% statistically?

76. You have been asked to determine if a sample is
representative of the general population in
terms of gender. Since there are roughly equal
numbers of men and women in the population,
your sample should have 50% females. However,
in your sample there are 65% females. How
much does your sample of 65% differ from the
hypothesized expectation of 50% statistically?
Since this question is dealing with
percentages or proportions, it will be
classified as a Difference Question

77. Examine the question or problem you are
working on.

78. Is it a question of goodness of fit?

79. If so, select GOODNESS OF FIT