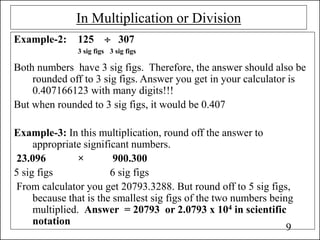
This document discusses rules for rounding numbers and calculations to the appropriate number of significant figures. It explains that in multiplication and division, the final answer should have the same number of significant figures as the term with the fewest significant figures. For addition and subtraction, the answer should have the same number of decimal places as the term with the fewest decimal places. When multiple operations are involved, rounding should occur only after all calculations are complete. Examples are provided to illustrate the various rules.

1. Chapter 2
Measurements and Calculations
Section 2.4
In this section of the chapter, you will learn about:
• Rounding off Numbers to appropriate significant
figures
• Rounding off when measurements are involved and
multiple operations are involved
1

2. Rules for Rounding Off
• Sometimes it becomes necessary that the
measurements, or the results of scientific calculations
need not carry all the digits, as the significant figures
are less than what your calculators might display.
• Therefore, the number needs to rounded off to correct
significant figures.
• We will learn how to do rounding off, for various
situations, and also in math calculations.
2

3. Rules for Rounding Off
• To round a number, first decide how many significant
figures the number should have.
• Once you know that, round off to that many digits.
• This would require removing the unwanted digits.
• If the digit to be removed is less than a value of 5,
the preceding digit stays the same
• Example, Round off 1.432 to three significant
figures. Answer is 1.43.
• We kept the 3 as it is, because the digit that was
removed was 2 (which is less than 5)
3

4. Rules for Rounding Off
If the digit to be removed is equal to or greater than 5,
the preceding digit is increased by 1
• Example-1: Round off 1.437 to three significant
figures.
• Answer is 1.44 (because the last digit being
removed is greater than 5)
Example-2: Round off 1.499 to 2 significant figures.
It becomes 1.5
4

5. Rules for Rounding Off
Don’t forget to add place-holding zeros if necessary,
in order to keep value the same!!
 For example, round off 1299 to two significant
figures. Answer is 1300 (it is not simply 13) and
to make it even more accurate, it is 1.3 x 103
 Example-3: Round of 999 to 2 significant
figures!!! It cannot be 1000 (ambiguous); but
1.0 x 103 is the correct answer.
5

6. Rounding Off: Examples
Round off the following numbers to 2
significant numbers:
1.54 = 1.5 (the digit 4 to be removed is less than
5)
1.69 = 1.7(the digit 9 to be removed is >5, and
therefore preceding digit 6 gets rounded off to
7)
0.0279027 = 0.028 or 2.8 x 10-2
159000 = 160000 or 1.6 x 105
19999 =20000 to be rounded off to 2.0 x 104
6

7. Rules for Significant Figures in Calculations
1) For multiplication or division, the number of
significant figures in the result is the same as that in
the measurement with the smallest number of
significant figures. (not the smallest value)
• Therefore, Count the number of significant figures in
each measurement
• Round the result so it has the same number of
significant figures as the measurement with the
smallest number of significant figures.
7

8. Rules for Significant Figures in Calculations
Example-1: 4.5 cm x 0.210 cm
2 sig figs 3 sig figs
Answer = 0.945 = when rounded is 0.95 cm2
2 sig figs
Notice that the number 4.5 has only 2 sig figs. And the
number 0.210 has 3 sig figs (trailing zero is significant
due to having decimal point in the measurement)
Hence the answer 0.945 should be rounded off to 2 sig
figs. Which would be 0.95
8

9. In Multiplication or Division
Example-2: 125  307
3 sig figs 3 sig figs
Both numbers have 3 sig figs. Therefore, the answer should also be
rounded off to 3 sig figs. Answer you get in your calculator is
0.407166123 with many digits!!!
But when rounded to 3 sig figs, it would be 0.407
Example-3: In this multiplication, round off the answer to
appropriate significant numbers.
23.096 × 900.300
5 sig figs 6 sig figs
From calculator you get 20793.3288. But round off to 5 sig figs,
because that is the smallest sig figs of the two numbers being
multiplied. Answer = 20793 or 2.0793 x 104 in scientific
notation
9

10. Rules for Significant Figures in Calculations
Rules For addition or subtraction: round your answer
so it should have as many decimal places as the
original number that has the FEWEST decimal
places.
12.11 mL+18.0mL+1.013mL = 31.123 mL = 31.1mL
Notice that the answer as only one decimal place.
Because, the number with smallest number of
decimal places is 18.0, with one decimal place.
10

11. Rules for Significant Figures in Calculations
Example-2: 13.77 + 908.226 = 921. 996 from calculator. But
when rounded off such that it has the same number of decimal
places as the smallest decimals of the two original numbers, then,
it will be 922.00
Example-3: 1,027 + 611 + 363.06 = 2001.06 from calculator.
But when rounded off, there should not be any decimal place,
because the original numbers 1027 or 611 do not have any decimal
places.
So the answer is 2001
11

12. Rules for Rounding Off in Calculations
• When multiple operations are involved (example
multiplication and a subtraction or addition) round
off at the end after all the operations are completed.
• Because if you keep rounding off in each step, it will
compound to too much error or inaccuracies.
• But while doing so, also remember that if there are
exact numbers (those obtained by counting or from
definitions), do not affect the number of significant
figures in an answer.
12

13. Rules for Rounding Off in Calculations
Example-1: 2 (1.008 g) + 15.99 g
First, we will complete the multiplication: 2 x 1.008 = 2.016 (has 4
significant figures because the number 2 is only an exact number,
did not come from measurement and does not play a role in
determining the significant figures.
Next, add the 2.016 with 15.99
2.016 + 15.99 ; your final answer should have only 2 decimal places,
because we apply the addition or subtraction rule.
Answer = 18.006g but rounded off to decimal places as 18.01g
13

14. Rules for Rounding Off in Calculations
Example-2: 137.3 s + 2(35.45) s (s stands for seconds, unit of
time measurement)
First carry out the multiplication 2 (35.45 s) = 70.90s
Next add this answer to the other number 137.3s
70.90s + 137.3 s = 208.20 s; should get rounded off to only the
10th place (because 137.3 has only 10th place decimal).
Answer is 208.2
14

15. Summary of Rounding off Rules
Here is the summary of all the rounding off rules:
• The rule in multiplication and division is that the final
answer should have the same number of significant
figures as there are in the number with the fewest
significant figures.
• The rule in addition and subtraction is that the answer
is given the same number of decimal places as the term
with the fewest decimal places.
15

16. Summary of Rounding off Rules
• When there is more than one operation involved, round
off at the end
• If the number to be dropped is greater than or equal to 5,
increase the number to its left by 1 (e.g. 2.9699 rounded
to three significant figures is 2.97).
• If the number to be dropped is less than 5, there is no
change (e.g. 4.00443 rounded to four significant figures is
4.004).
16