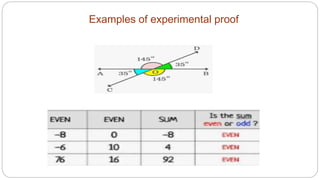
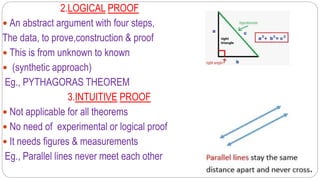
This document discusses the meaning, nature, and types of mathematical proofs. It defines a proof as a rigorous argument used to establish the truth of a mathematical statement. Proofs can be direct or indirect. Direct proofs establish a conclusion logically by moving from the known to the unknown. Indirect proofs establish a conclusion by assuming it is false and reaching a contradiction. The document provides examples of different types of direct proofs like experimental, logical, and intuitive proofs. It also discusses types of indirect proofs like proof by contradiction, proof by exhaustion, and non-constructive proofs.

1. K.L.E.SOCIETY’S, COLLEGE OF EDUCATION
VIDYANAGAR, HUBBALLI-31
POSS MATHEMATICS
TOPIC: PROOF-MEANING,NATURE,TYPES
submitted to submitted by
Shri.VEERESH.A.KALAKERI Mr.R.PRAKASH BABU
LECTURER B.Ed., 1st Semester

2. PROOF- MEANING & NATURE
 MEANING:
 The word “proof “comes from the Latin word
“probare” means “to test“
 NATURE:
 Aesthetic, logical deductive
 arguments for mathematical
 statements
 A rigorous argument to convince
 the truth of a statement
Proofs are “theorems” & “axioms”

3. DIRECT PROOF – TYPES & EXAMPLES
 Conclusion is established logically.
 Used to prove arithmetic sums,algebraic expressions & geometrical
theorems
Eg., The sum of two even integer
Is always even
TYPES: 1. EXPERIMENTAL PROOF
 Theoretical argument is replaced by practical process.
 Logic from known to unknown( Deductive approach)
 Eg., The vertical opposite angles are equal.

4. Examples of experimental proof

5. 2.LOGICAL PROOF
 An abstract argument with four steps,
The data, to prove,construction & proof
 This is from unknown to known
 (synthetic approach)
Eg., PYTHAGORAS THEOREM
3.INTUITIVE PROOF
 Not applicable for all theorems
 No need of experimental or logical proof
 It needs figures & measurements
Eg., Parallel lines never meet each other

6. INDIRECT PROOF- TYPES &EXAMPLES
 Used to prove proposition which cannot be proved by direct
proof
 Looks for a contradiction to its original assumption
TYPES: 1.PROOF BY CONTRADICTION :
 Starts the stated conclusion assuming to be untrue,for the
same of reasoning & reaches absurdity to infer that the
assumption is wrong or untrueEg.,Two adjacent angles are
supplementary, then they are in the same straight line

7. 2. PROOF BY EXHAUSTION
 Conclusion is established by dividing into many number of cases proving each
separately
 Possibility of exhaustion shown by contrary
 One possible left is accepted.
 E.g., If two angles of a triangle are unequal,
 the greater angle has the greater side opposite to it
3. NON-CONSTRUCTIVEPROOF
 A proof by contradiction in which the non-existence of the object is proved to be
impossible.
 E.g., There exists two irrational numbers a & b such that is a rational number