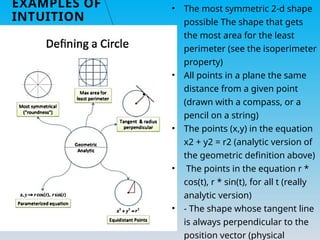
The document discusses intuition, proof, and certainty in mathematics, defining intuition as immediate understanding without reasoning and emphasizing its role in problem-solving. It explains various proof techniques including direct proof, proof by contradiction, induction, and contrapositive, illustrated with examples. Certainty is defined as the quality of being reliably true, while Polya's problem-solving strategy outlines a four-step method: understand the problem, devise a plan, carry out the plan, and review the solution.

1. INTUITION, PROOF, AND
CERTAINTY

2. TOPICS
- What is intuition?
- Examples of intuition
- What is Proof?
- Examples of Proof
- What is certainty?
- Polya’s Problem Solving Strategy
2

3. WHAT IS INTUITION?
• INTUITION IS AN IMMEDIATE UNDERSTANDING OR KNOWING
SOMETHING WITHOUT REASONING
• INTUITION IS THAT FEELING IN YOUR GUT WHEN YOU
INSTINCTIVELY KNOW THAT SOMETHING YOU ARE DOING IS
RIGHT OR WRONG
• AN IMMEDIATE UNCONSCIOUS PERCEPTION
• DIRECT UNDERSTANDING OF TRUTHS - INDEPENDENCE OF
ANALYTICAL PROCESS A NON-LINEAR PROCESS OF KNOWING
THROUGH PHYSICAL AWARENESS, EMOTIONAL AWARENESS,
AND MAKING CONNECTION BETWEEN THEM
• AN IRRATIONAL UNCONSCIOUS TYPE OF KNOWING

4. WHAT IS INTUITION?
• There are a lot of definition of an intuition and one of these is that
it is an immediate understanding or knowing something without
reasoning.
• It does not require a big picture or full understanding of the
problem, as it uses a lot of small pieces of abstract information that
you have in your memory to create a reasoning leading to your
decision just from the limited information you have about the
problem in hand. Intuition comes from noticing, thinking and
questioning.
• As a student, you can build and improve your intuition by doing the
following: a. Be observant and see things visually towards with your
critical thinking.
• B. Make your own manipulation on the things that you have noticed
and observed.
• C. Do the right thinking and make a connections with it before
doing the solution.

5. EXAMPLES OF
INTUITION
• The most symmetric 2-d shape
possible The shape that gets
the most area for the least
perimeter (see the isoperimeter
property)
• All points in a plane the same
distance from a given point
(drawn with a compass, or a
pencil on a string)
• The points (x,y) in the equation
x2 + y2 = r2 (analytic version of
the geometric definition above)
• The points in the equation r *
cos(t), r * sin(t), for all t (really
analytic version)
• - The shape whose tangent line
is always perpendicular to the
position vector (physical

6. 1. Based on the given picture below, which among of the two
yellow lines is longer? Is it the upper one or the lower one?
6
The figure above is called Ponzo illusion (1911). There are two identical
yellow lines drawn horizontally in a railway track. If you will be observing
these two yellow lines, your mind tells you that upper yellow line looks
longer that the below yellow line. But in reality, the two lines has equal
length. For sure, you will be using a ruler to be able to determine which
of the two is longer than the other one. The exact reasoning could goes
like this. The upper yellow line looks longer because of the converging
sides of a railway. The farther the line, it seems look line longer that the
other yellow line below.

7. WHAT IS PROOF AND
CERTAINTY?
• By definition, a proof is an inferential argument for a
mathematical statement while proofs are an example
of mathematical logical certainty.
• A proof in mathematics is a convincing argument that
some mathematical statement is true. A proof should
contain enough mathematical detail to be convincing
to the person(s) to whom the proof is addressed
Proof Techniques used in Mathematics
 Direct Proof
 Proof by contradiction
 Proof by induction
 Proof by contrapositive

8. Examples of direct proof
► proof :the sum of any two consecutive numbers is odd
• 2+3 = odd
• 4+5 =odd
first, we define some definition:
definition 1: integer is even if n = 2k
definition 2: integer is odd if n = 2k +1
definition 3: two consecutive integers a and b are
consecutive if b = a+1
let a = integer
let b = consecutive integer = a+1
sum :
a + b
a + a+1
2a+1
based on our definition 2: integer is odd if n = 2k +1
therefore, we have a direct proof that the sum of two
consecutive integer is odd.
8

9. Example of Proof by Contradiction
• Proof
– Assume that a and b are consecutive integers
Assume that (a + b) is not odd, then no integer k such
that (a+b) = 2k+ 1
- Sum :
a + b
a + a +1
Statement 1: 2a+1
Statement 2: (a + b) = 2k+1
If k is not an integer, then why (a+b) = 2a+1, where a is an
integer??
These statements are contradicting!

10. Example of Proof by Induction
• Proof
- The sum of any two consecutive numbers is odd.
- 1+2 = 3 -> odd
- 5+6 = 11 -> odd
- 7+ 8 = 15 -> odd
Based on observations, (inductive reasoning) we have
proven that the sum of any two consecutive numbers is
odd

11. Example of Proof by Contrapositive
• Proof
- If the sum of (a + b) is NOT odd, then a and b are NOT
consecutive numbers
Make a statement that is consecutive and check the sum - We
know that (a + b) = K + (K+1) = 2k+1 K does not hold for any
integer K. K +1 is the successor of K. In order for
- • Therefore, we have proven that The sum of any two
consecutive numbers should be odd

12. Certainty
• the quality of being reliably true. Certainty is the
state of being definite or of having no doubts at all
about something
•examples:
probability is the branch of mathematics
concerning numerical descriptions of how likely an
event is to occur, or how likely it is that a
proposition is true.
The probability of an event is a number between 0
and 1, where, roughly speaking, 0 indicates
impossibility of the event and 1 indicates certainty

13. POLYA’S FOUR STEPS
IN PROBLEM SOLVING

14. • George Polya is one of the foremost recent mathematicians
to make a study of problem solving.
• He was born in Hungary and moved to the United States in
1940.
• He is also known as “The Father of Problem Solving”.
• He made fundamental contributions to combinatorics,
number theory, numerical analysis and probability theory.
• He is also noted for his work in heuristics and mathematics
education.
• Heuristic, a Greek word means that "find" or "discover" refers
to experience-based techniques for problem solving,
learning, and discovery that gives a solution which is not

15. 15
THE GEORGE POLYA’S PROBLEM-
SOLVING METHOD ARE AS FOLLOWS:
Step 1. Understand the Problem.
Step 2. Devise a Plan
Step 3. Carry out the plan
 Step 4. Look back or Review the
Solution

16. 16
THE GEORGE POLYA’S PROBLEM-
SOLVING METHOD ARE AS FOLLOWS:
Step 1. Understand the Problem.
Step 2. Devise a Plan
Step 3. Carry out the plan
 Step 4. Look back or Review the
Solution

17. THANK YOU
17