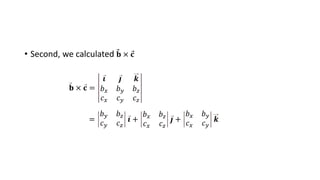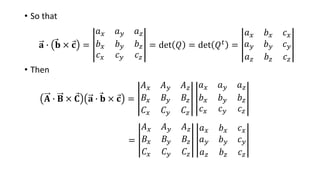The document proves the vector identity A ∙ B × C = a ∙ b × c by showing that both sides are equal to the determinant of the same matrix P. It first defines the vectors A, B, C, a, b, c and computes B × C and b × c. It then calculates A ∙ B × C and a ∙ b × c, showing they are both equal to det(P). It further shows that det(P) = det(PQt) by properties of determinants and transposes, proving the original identity.