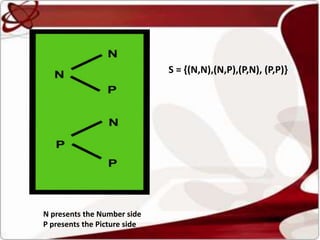
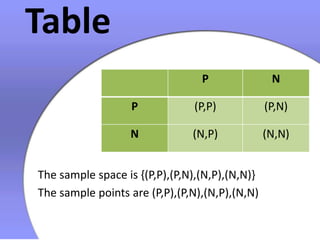
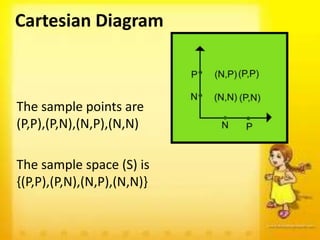
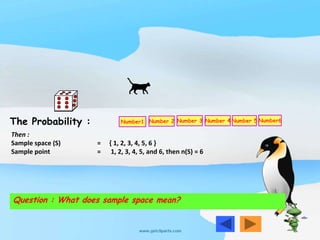
There are four ways to determine the sample space of an experiment: listing all possible outcomes, using a tree diagram, displaying the outcomes in a table, or with a Cartesian diagram. The document provides examples of determining the sample space of coin tosses using each of these methods. The sample space represents all possible outcomes of an experiment.

1. Determining the Sample Space
There are four ways to determine the sample
space, those are:
1. Listing
2. Tree Diagram
3. Table
4. Cartesian Diagram

2. Listing
We have a coin which have number side and
picture side. The sample space are :
S={N,P}
n(S)=2

3. Tree Diagram
We have a coin which have number side and
picture side. Then, we throw it for two times
We can find the sample space by using tree
diagram like this one.

4. N presents the Number side
P presents the Picture side
S = {(N,N),(N,P),(P,N), (P,P)}

5. Table
P N
P (P,P) (P,N)
N (N,P) (N,N)
The sample space is {(P,P),(P,N),(N,P),(N,N)}
The sample points are (P,P),(P,N),(N,P),(N,N)

6. Cartesian Diagram
The sample points are
(P,P),(P,N),(N,P),(N,N)
The sample space (S) is
{(P,P),(P,N),(N,P),(N,N)}

7. Look at the coin which has number side and picture side.
Picture side(P) Number side(N)
Then :
Sample space (S) = { N , P }
Sample point = N and P, then n(S) = 2
example

8. Then :
Sample space (S) = { 1, 2, 3, 4, 5, 6 }
Sample point = 1, 2, 3, 4, 5, and 6, then n(S) = 6
The Probability : Number1 Number 2 Number 3 Number 4 Number 5 Number6
Question : What does sample space mean?