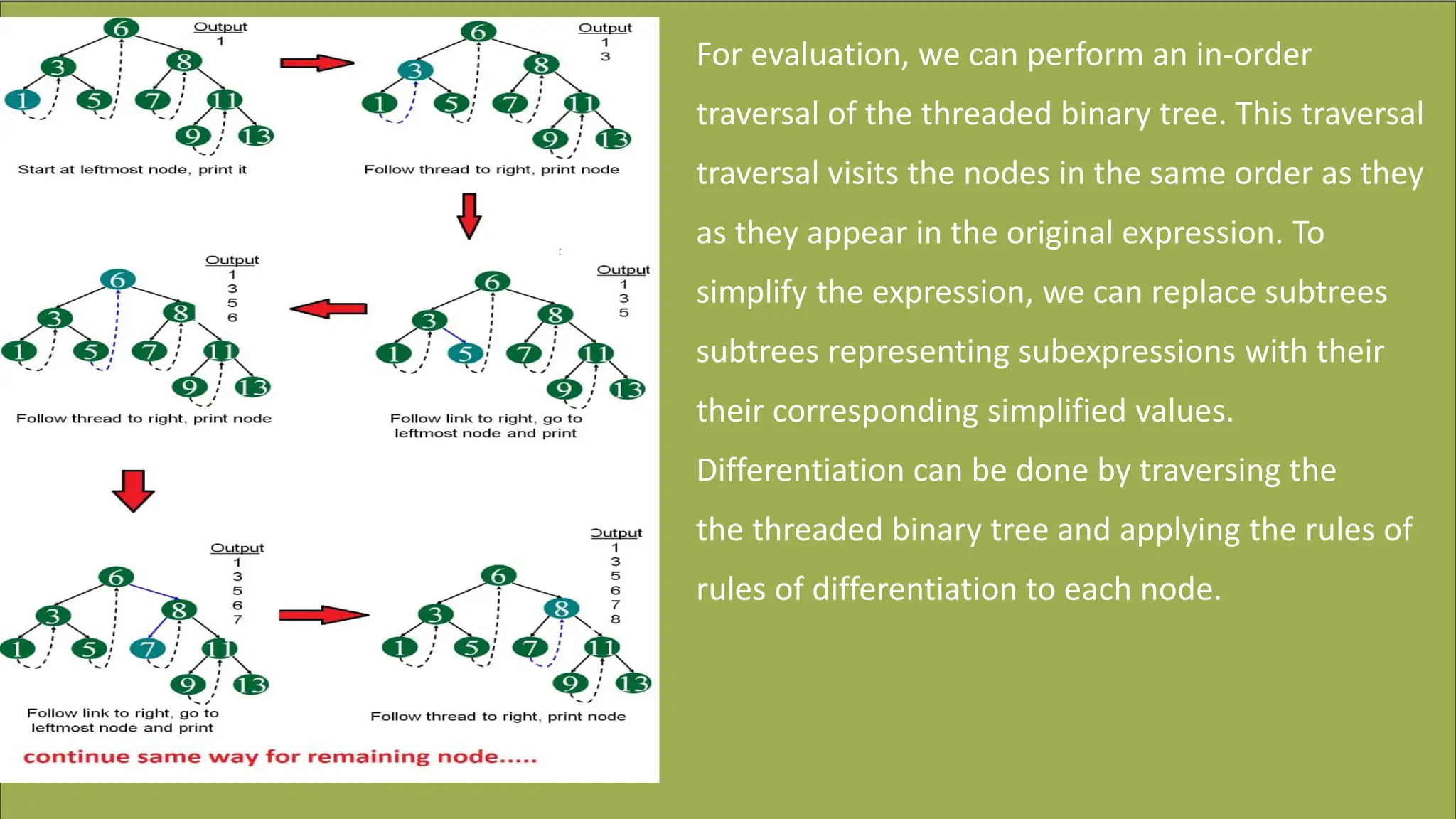
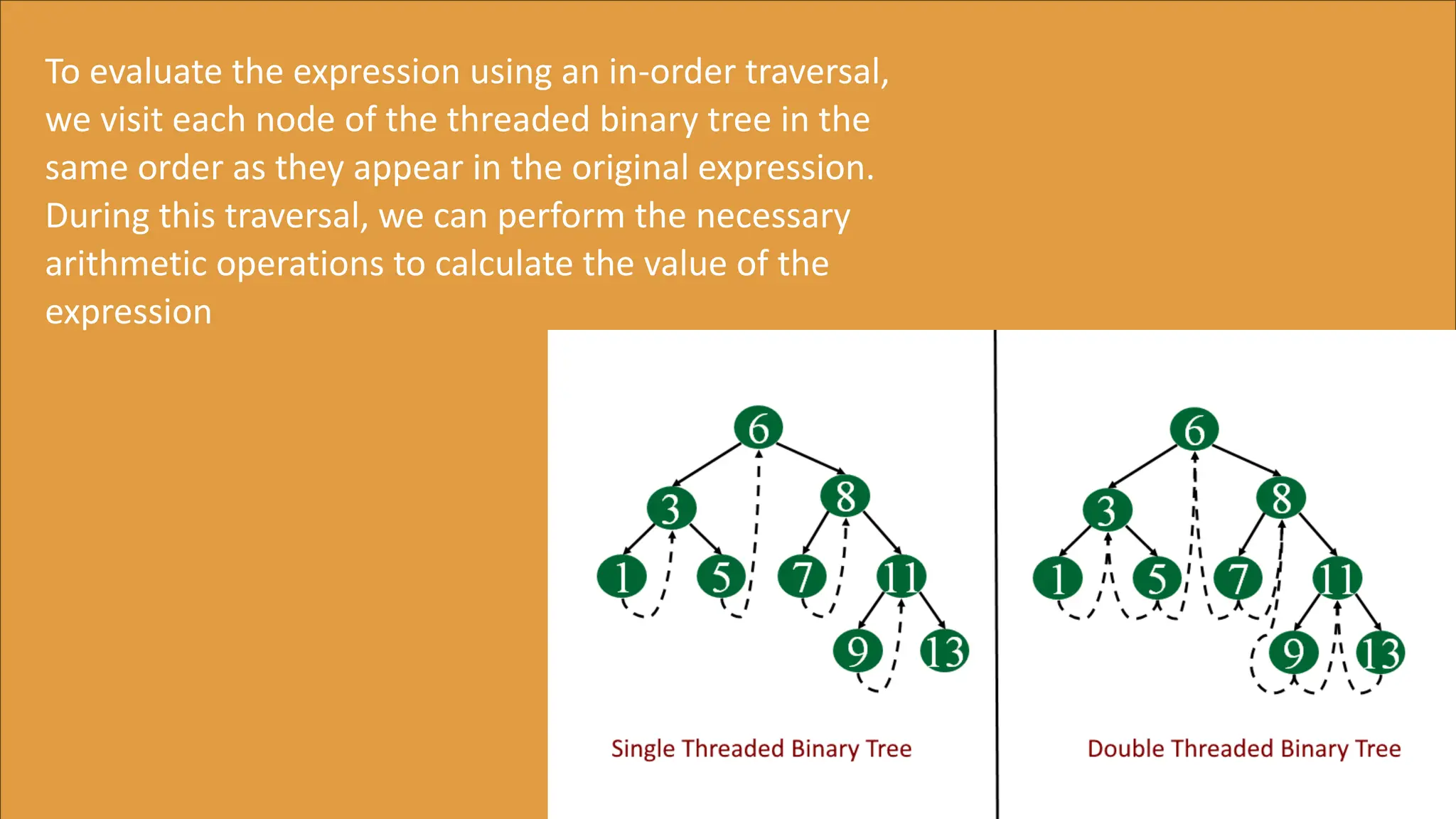
The document discusses the use of threaded binary trees for representing and manipulating algebraic expressions. It explains the definition and purpose of threaded binary trees, describes the conversion of infix expressions to these trees, and outlines methods for evaluation and manipulation, including simplification and differentiation. Potential limitations of this approach are also mentioned, noting that while efficient, threaded binary trees may lack intuitiveness and can struggle with complex expressions.

1. Tree Traversal
Representation of
Algebraic Expression in
Threaded Binary Trees
Welcome to our presentation on using threaded binary trees to represent
represent algebraic expressions. Learn how traversing these trees aids in
in expression manipulation.
SR

2. Binary Trees: A Quick Introduction
1 Anatomy of a Binary Tree
A binary tree is a hierarchical data
structure composed of nodes, each
holding a value and having at most two
child nodes.
2 Tree Traversal
Tree traversal refers to the process of
visiting every node in a tree data
structure exactly once using a specific
order or pattern.
3 Understanding Algebraic Expressions
An algebraic expression is a collection of variables, constants, and mathematical
mathematical operations. It can be represented using traditional infix notation.
notation.

3. Threaded Binary Trees: Definition and
Purpose
1 Definition
A threaded binary tree is a binary tree
tree that contains additional links that
that connect certain nodes to their in
their in-
-
order predecessors or
successors.
2 Purpose
Threaded binary trees provide an
efficient way to traverse and
manipulate binary trees without the
the need for recursive calls or stack
stack space.
3 Types of Threaded Binary Trees
There are two main types of threaded binary trees: single-threaded (or simply threaded)
threaded) and double-threaded (or fully-threaded).

4. Representing Algebraic Expressions in
Threaded Binary Trees
1 Conversion Algorithm
We can convert the infix notation of an algebraic expression into a threaded binary tree using
binary tree using a modified version of the infix to postfix algorithm.
2 Example Representation
Let's take the algebraic expression "2 * (3 + 4)" and walk through the steps of converting it into
converting it into a threaded binary tree.
3 Expression Evaluation and Manipulation
Once the expression is represented as a threaded binary tree, we can easily evaluate it or
evaluate it or perform various manipulations such as simplification or differentiation.
differentiation.

5. Threaded binary trees allow for efficient
traversal and manipulation of binary
trees, eliminating the need for recursive
calls or stack space. By converting an
algebraic expression into a threaded
binary tree, we can easily evaluate the
expression and perform operations such
as simplification or differentiation.

6. For evaluation, we can perform an in-order
traversal of the threaded binary tree. This traversal
traversal visits the nodes in the same order as they
as they appear in the original expression. To
simplify the expression, we can replace subtrees
subtrees representing subexpressions with their
their corresponding simplified values.
Differentiation can be done by traversing the
the threaded binary tree and applying the rules of
rules of differentiation to each node.
This Photo by Unknown Author is licensed under CC
BY-NC

7. To evaluate the expression using an in-order traversal,
we visit each node of the threaded binary tree in the
same order as they appear in the original expression.
During this traversal, we can perform the necessary
arithmetic operations to calculate the value of the
expression

8. One potential limitation of using threaded
threaded binary trees for expression
evaluation is that they may not be as intuitive
intuitive to read and understand compared to
compared to other data structures.
Additionally, threaded binary trees may not
not be the best choice for evaluating
expressions with extremely complex or
nested subexpressions.

9. Algebraic expression of binary trees:
Algebraic expression trees represent expressions that contain numbers,
contain numbers, variables, and unary and binary operators. Some of the
Some of the common operators are × (multiplication), ÷
(division), + (addition), − (subtraction), ^ (exponentiation), and
(division), +
and –
–
(negation). The operators are contained in the internal nodes of
nodes of the tree, with the numbers and variables in the leaf nodes
nodes.
.
The nodes of binary operators have two child nodes, and the
The
and the unary operators have one child node. expression tree for 7 + ((1+8)*3) would be:

10. By
P.Shiva charan
reddy(23915a0515)
Vasavi(23915a0516)
Rafath(23915a0517)