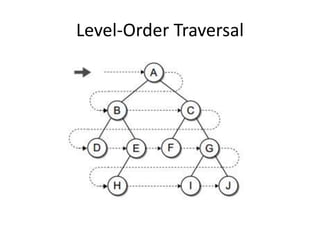
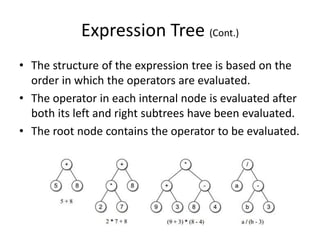
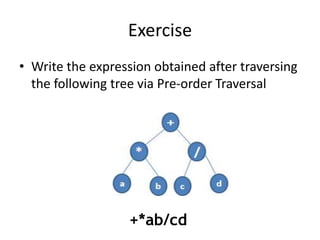
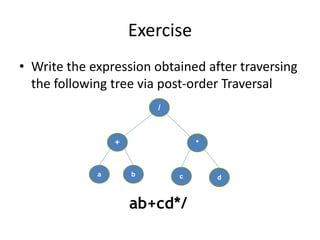
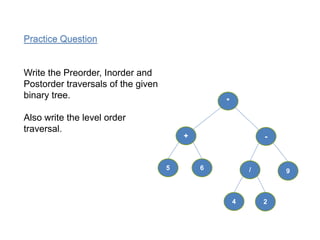
This document discusses different types of tree traversals including preorder, inorder, postorder, and breadth-first traversals. It explains that preorder, inorder, and postorder traversals are examples of depth-first traversals as they traverse nodes deeper in the tree before moving to higher levels, while breadth-first traversal visits nodes by level from left to right. The document also covers expression trees, which represent arithmetic expressions as binary trees with operators in interior nodes and operands in leaves.

1. Data Structures and Algorithms
Trees - II

2. Outline
• Binary Tree Revision
• Traversing a Binary Tree
– Depth-first
• Pre-order
• In-order
• Post-order
– Breadth-first

3. Tree Traversal
• A traversal iterates through a collection, one item at a time, in
order to access or visit each item.
• With a linear structure such as a linked list, the traversal is
rather easy since we can start with the first node and iterate
through the nodes, one at a time, by following the links
between the nodes.
• But how do we visit every node in a binary tree?

4. Linked Implementation

5. Pre-order Traversal
Since every node is the
root of its own subtree,
we can repeat the same
process on each node,
resulting in a
recursive solution.
(Also called NLR traversal)

6. In-order Traversal
(Also called LNR traversal)

7. Post-Order Traversal
(Also called LRN traversal)

8. Depth-First and Breadth-First Traversal
• The preorder, inorder, and postorder traversals are
all examples of a depth-first traversal.
– That is, the nodes are traversed deeper in the tree
before returning to higher-level nodes.
• Another type of traversal that can be performed on
a binary tree is the level order traversal which is
known as breadth-first traversal.
– That is, the nodes are visited by level, from left to right.

9. Level-Order Traversal

10. Expression Trees
• Arithmetic expressions such as (9+3)*(8 4) can be
represented using an expression tree.
• An expression tree is a binary tree in which the
operators are stored in the interior nodes and the
operands (the variables or constant values) are
stored in the leaves.
• Once constructed, an expression tree can be used
to evaluate the expression or for converting an
infix expression to either pre-fix or post-fix
notation.

11. Expression Tree (Cont.)
• The structure of the expression tree is based on the
order in which the operators are evaluated.
• The operator in each internal node is evaluated after
both its left and right subtrees have been evaluated.
• The root node contains the operator to be evaluated.

12. +*ab/cd
Exercise
• Write the expression obtained after traversing
the following tree via Pre-order Traversal

13. a+b+c+d
Exercise
• Write the expression obtained after traversing
the following tree via in-order Traversal

14. ab+cd*/
Exercise
• Write the expression obtained after traversing
the following tree via post-order Traversal
/
+
d
c
b
a
*

15. *
+
9
/
6
5
Practice Question
Write the Preorder, Inorder and
Postorder traversals of the given
binary tree.
Also write the level order
traversal.
-
2
4

16. References
• Data Structures and Algorithms Using Python, Rance D.
Necaise, John Wiley & Sons, Inc. 2010
• John R. Hubbard, Data Structures with Java (Schaum's Outline
Series), McGraw-Hill Education; 2nd edition (June 16, 2009)