The document discusses extended binary trees, which utilize external nodes to replace null subtrees, making it easier to calculate weighted path lengths and convert binary trees into complete binary trees. It also explores algebraic expressions, explaining infix, prefix, and postfix notations, along with their implementation in C and C++ programs. Finally, it illustrates the generation of expression trees through examples, highlighting the process of evaluating mathematical expressions.

1. DATA
STRUCTURE
TOPIC
ALGEBRAIC EXPRESSIOS, EXTENDED BINARY TREES
SUBMITTED BY
PRITAM KUMAR GHOSH (EN22CS301756)
PUSHPRAJ SINGH CHOUHAN(EN22CS301774)

2. EXTENDED BINARY TREES
INTRODUCTION
Extended binary tree is a type of binary tree in which all the null sub tree of the
original tree are replaced with special nodes called external nodes whereas other
nodes are called internal nodes

3. Properties of External binary tree
1.The nodes from the original tree are internal nodes and the special
nodes are external nodes.
2.All external nodes are leaf nodes and the internal nodes are non-leaf
nodes.
3.Every internal node has exactly two children and every external node
is a leaf. It displays the result which is a complete binary tree.

4. Application of extended binary tree:
1.Calculate weighted path length: It is used to calculate total path length in case of
weighted tree.
2.Here, the sum of total weights is already calculated and stored in the external nodes
and thus makes it very easier to calculate the total path length of a tree with given
weights. The same technique can be used to update routing tables in a network.
3.To convert binary tree in Complete binary tree: The above-given tree having
removed all the external nodes, is not a complete binary tree. To introduce any tree
as complete tree, external nodes are added onto it. Heap is a great example of a
complete binary tree and thus each binary tree can be expressed as heap if external
nodes are added to it.

5. C# program to make an extended binary tree
// C++ program to make an extended binary
tree
#include <bits/stdc++.h>
using namespace std;
// A Tree node
struct Node {
int key;
struct Node *left, *right;
};
// Utility function to
// create a new node
Node* newNode(int key)
{
Node* temp = new Node;
temp->key = key;
temp->left = temp->right = NULL;
return (temp);
}

6. Output:
-1 5 -1 2 -1 1 -1 3 -1 4 -1
// Function for inorder
traversal
void traverse(Node* root)
{
if (root != NULL) {
traverse(root->left);
cout << root->key << "
";
traverse(root->right);
}
else {
// Making external
nodes
root = newNode(-1);
cout << root->key << "
";
}
}
// Driver code
int main()
{
Node* root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left =
newNode(5);
root->right->right = newNode(4);
traverse(root);
return 0;
}

7. ALGEBRAIC EXPRESSIOS
When you write an arithmetic expression such as B * C, the form of the expression
provides you with information so that you can interpret it correctly. In this case we
know that the variable B is being multiplied by the variable C since the multiplication
operator * appears between them in the expression. This type of notation is referred to
as infix since the operator is in between the two operands that it is working on.
Different algebraic expression are:
Prefix expression notation requires that all operators precede the two operands that
they work on. Postfix, on the other hand, requires that its operators come after the
corresponding operands.

8. Examples of Infix, Prefix, and Postfix

9. An Expression with Parentheses

10. Additional Examples of Infix, Prefix, and
Postfix

11. Implementation of Expression tree in C Programming
language
// C program for expression tree implementation
#include <stdio.h>
#include <stdlib.h>
/* The below structure node is defined as a node of a binary tree consists
of left child and the right child, along with the pointer next which points to the next node */
struct node
{
char info ;
struct node* l ;
struct node* r ;
struct node* nxt ;
};
struct node *head=NULL;
/* Helper function that allocates a new node with the
given data and NULL left and right pointers. */
struct node* newnode(char data)

12. {
struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ;
node->info = data ;
node->l = NULL ;
node->r = NULL ;
node->nxt = NULL ;
return ( node ) ;
}
void Inorder(struct node* node)
{
if ( node == NULL)
return ;
else
{
/* first recur on left child */
Inorder ( node->l ) ;
/* then print the data of node */
printf ( "%c " , node->info ) ;
/* now recur on right child */
Inorder ( node->r ) ;
}
}

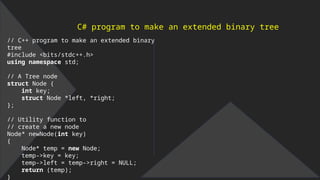
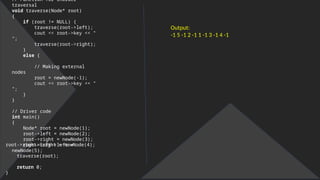
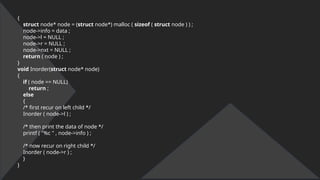
13. void push ( struct node* x )
{
if ( head == NULL )
head = x ;
else
{
( x )->nxt = head ;
head = x ;
}
// struct node* temp ;
// while ( temp != NULL )
// {
// printf ( " %c " , temp->info ) ;
// temp = temp->nxt ;
// }
}
struct node* pop()
{
// Poping out the top most [pointed with head] element
struct node* n = head ;
head = head->nxt ;
return n ;
}
int main()
{
char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ;
int n = sizeof(t) / sizeof(t[0]) ;
int i ;
struct node *p , *q , *s ;
for ( i = 0 ; i < n ; i++ )

14. for ( i = 0 ; i < n ; i++ )
{
// if read character is operator then popping two
// other elements from stack and making a binary
// tree
if ( t[i] == '+' || t[i] == '-' || t[i] == '*' || t[i] == '/' || t[i] == '^' )
{
s = newnode ( t [ i ] ) ;
p = pop() ;
q = pop() ;
s->l = q ;
s->r = p;
push(s); }
else {
s = newnode ( t [ i ] ) ;
push ( s ) ; } }
printf ( " The Inorder Traversal of Expression Tree: " ) ;
Inorder ( s ) ;
return 0 ; }

15. Let’s understand the process of generation of an expression tree intuitively using the expression tree described in
the previous section.
Expression: A * B + C / D
Scan the expression and according to the associativity and precedence find the operator which will be evaluated
at last.
In our example, the + operator will be evaluated in the last so keep it as the root node and divide the remaining
expression into left and right subtrees.
Generation of Expression Tree
After solving the right and left subtree our final expression tree would become like the image given below:

16. Thank you