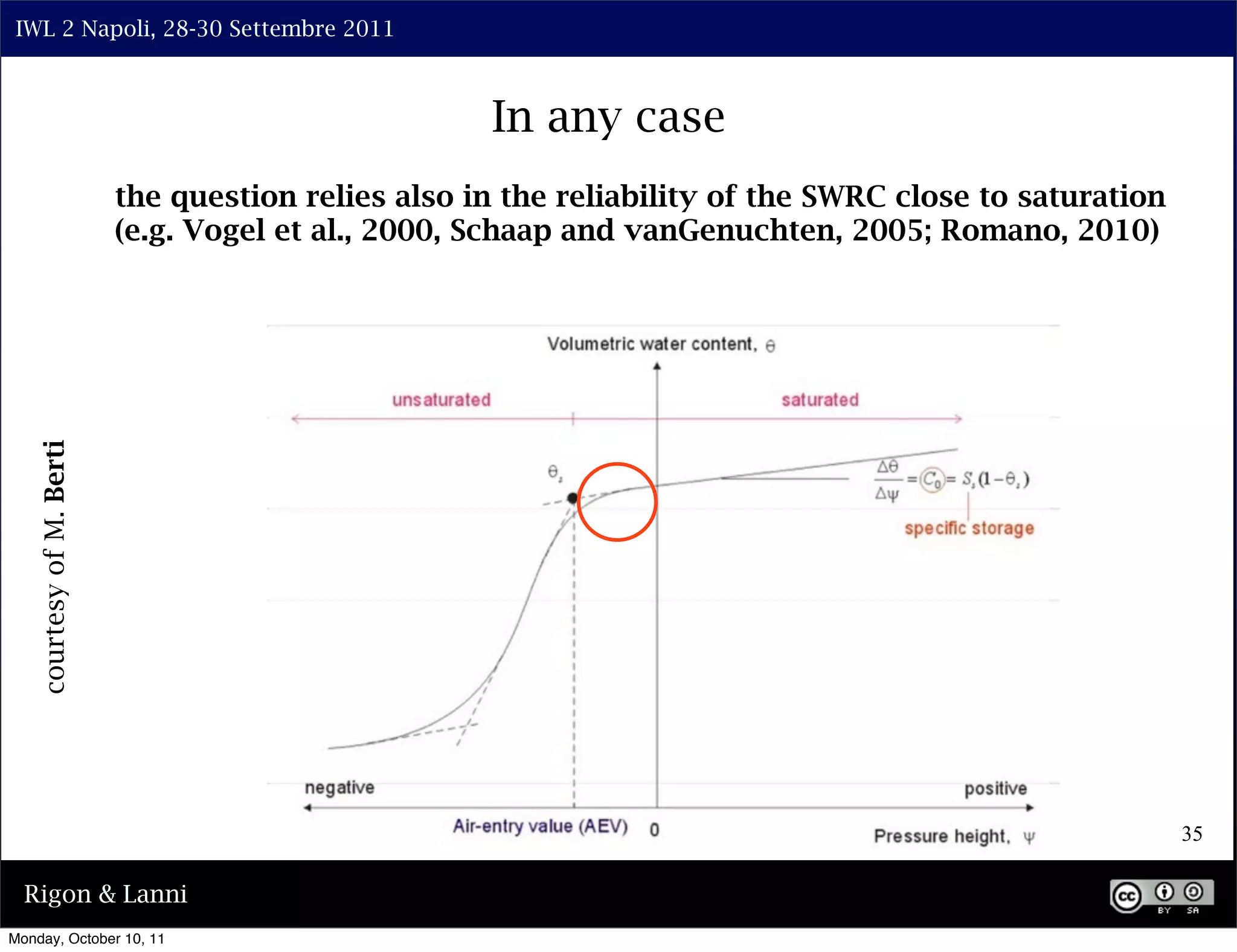
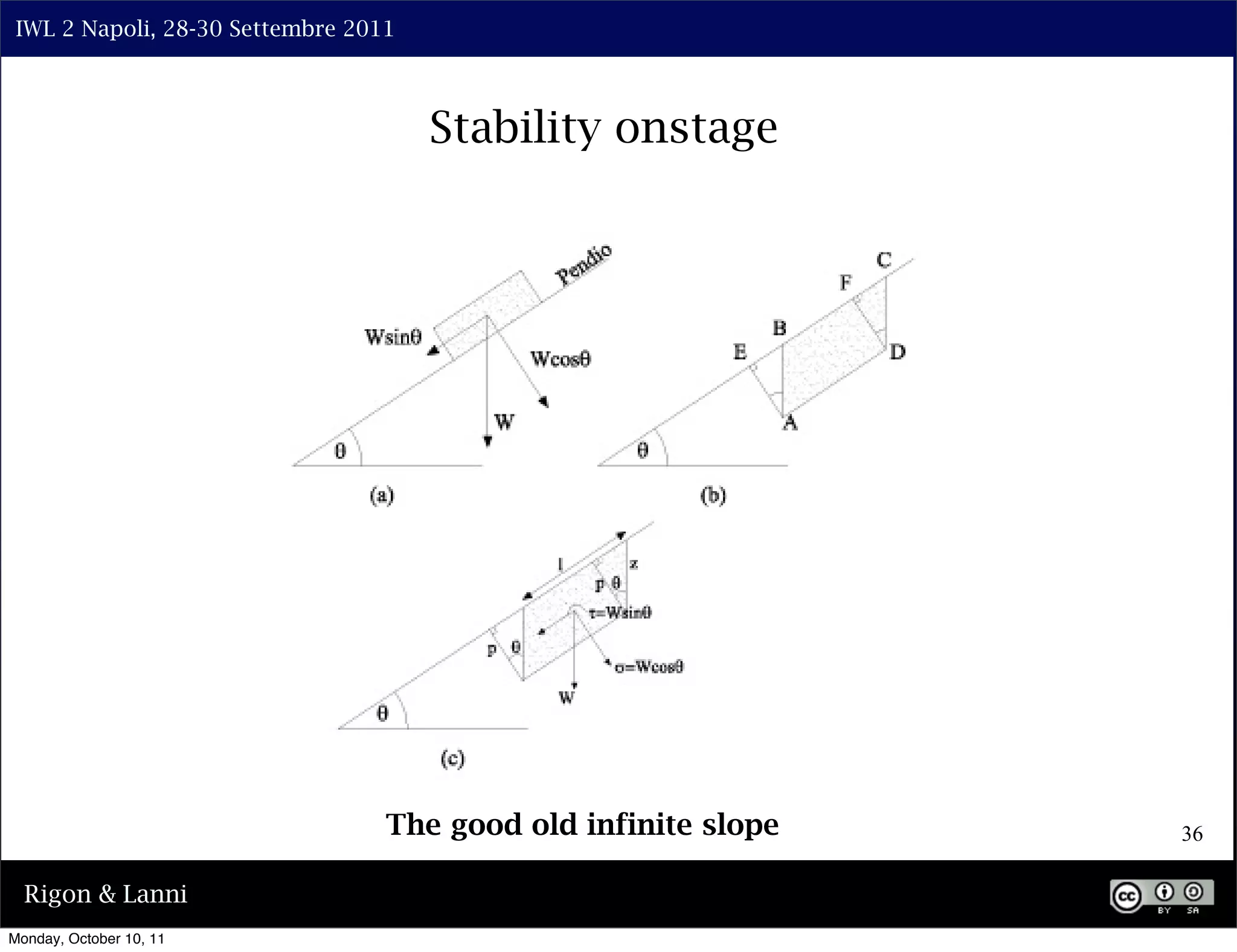
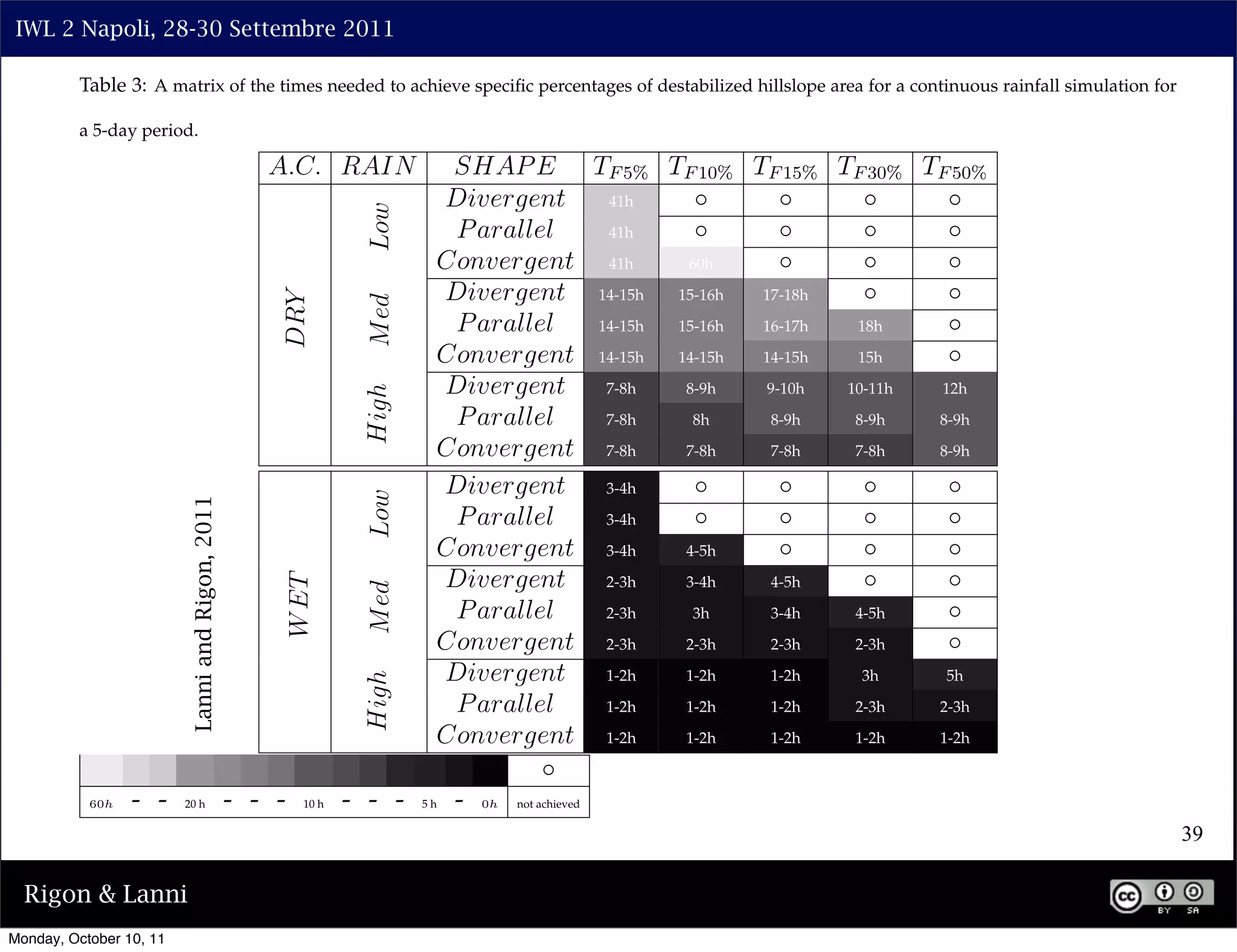
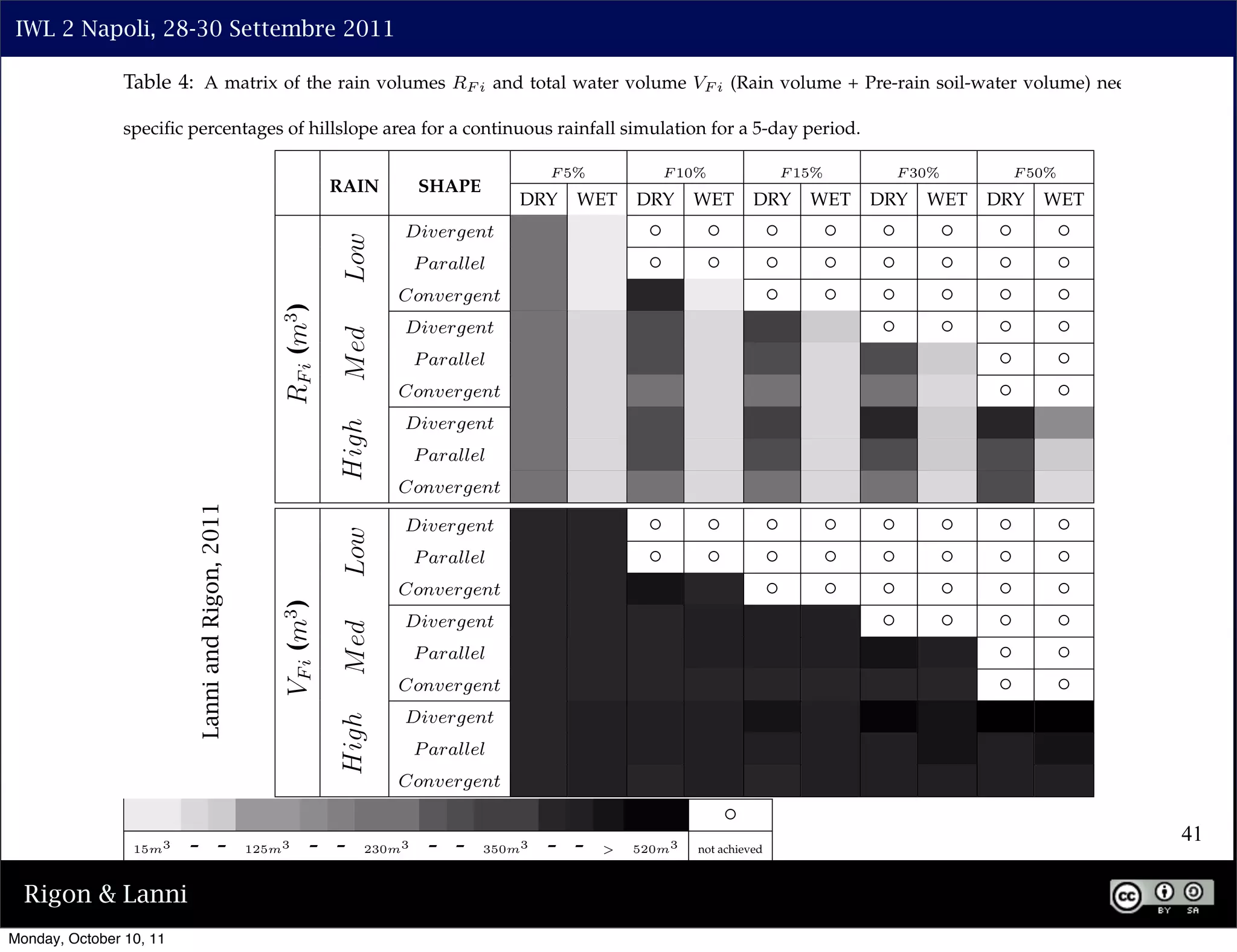
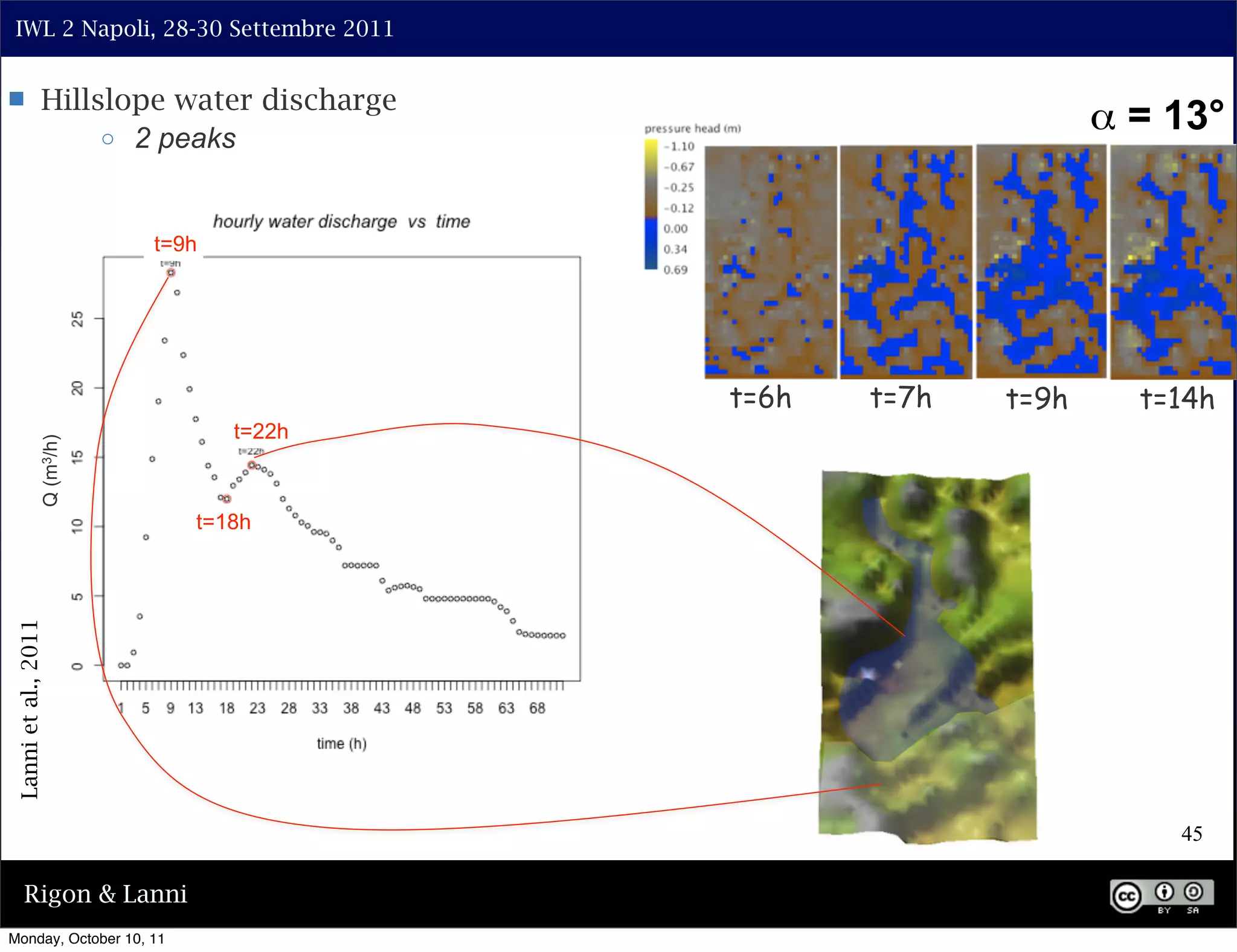
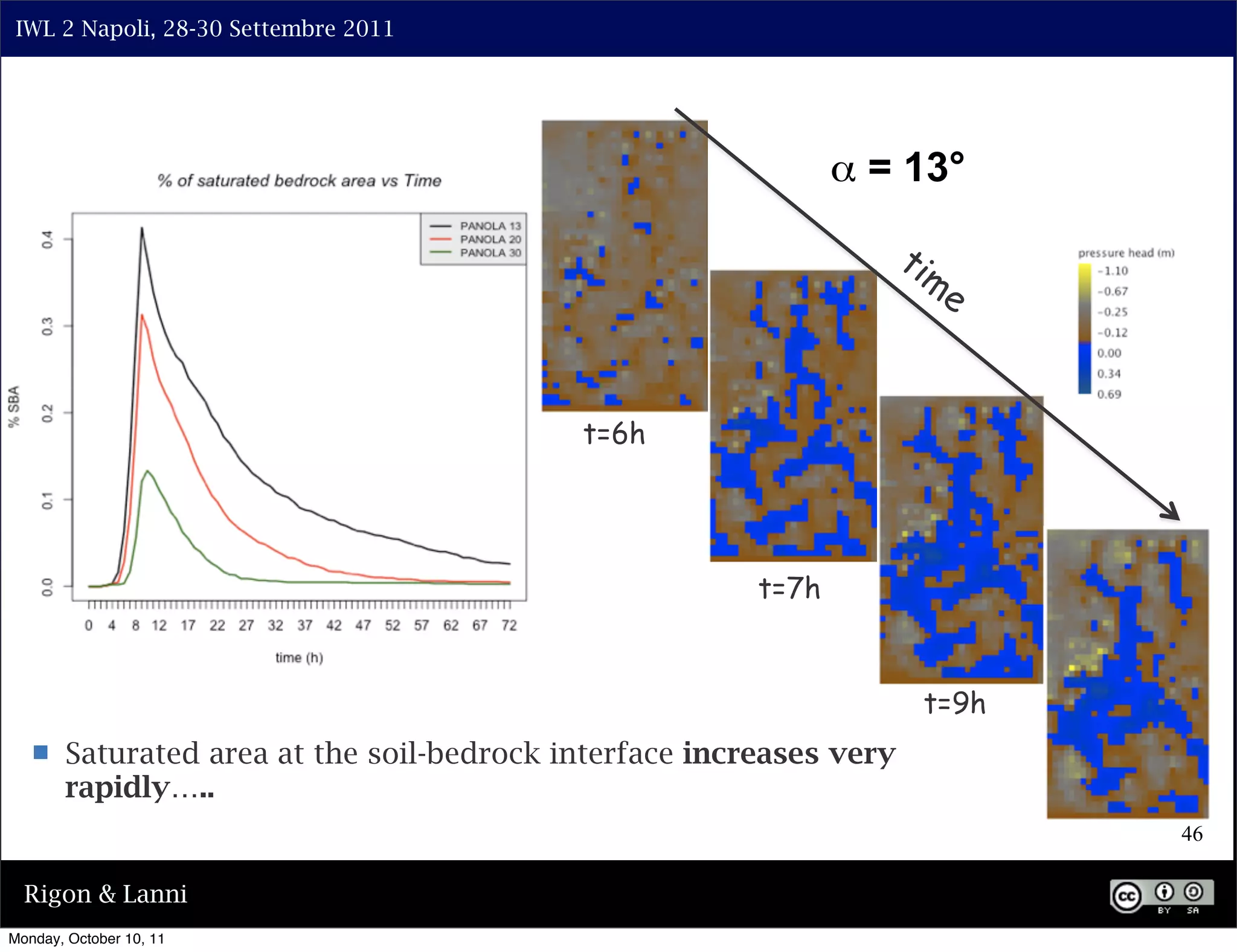
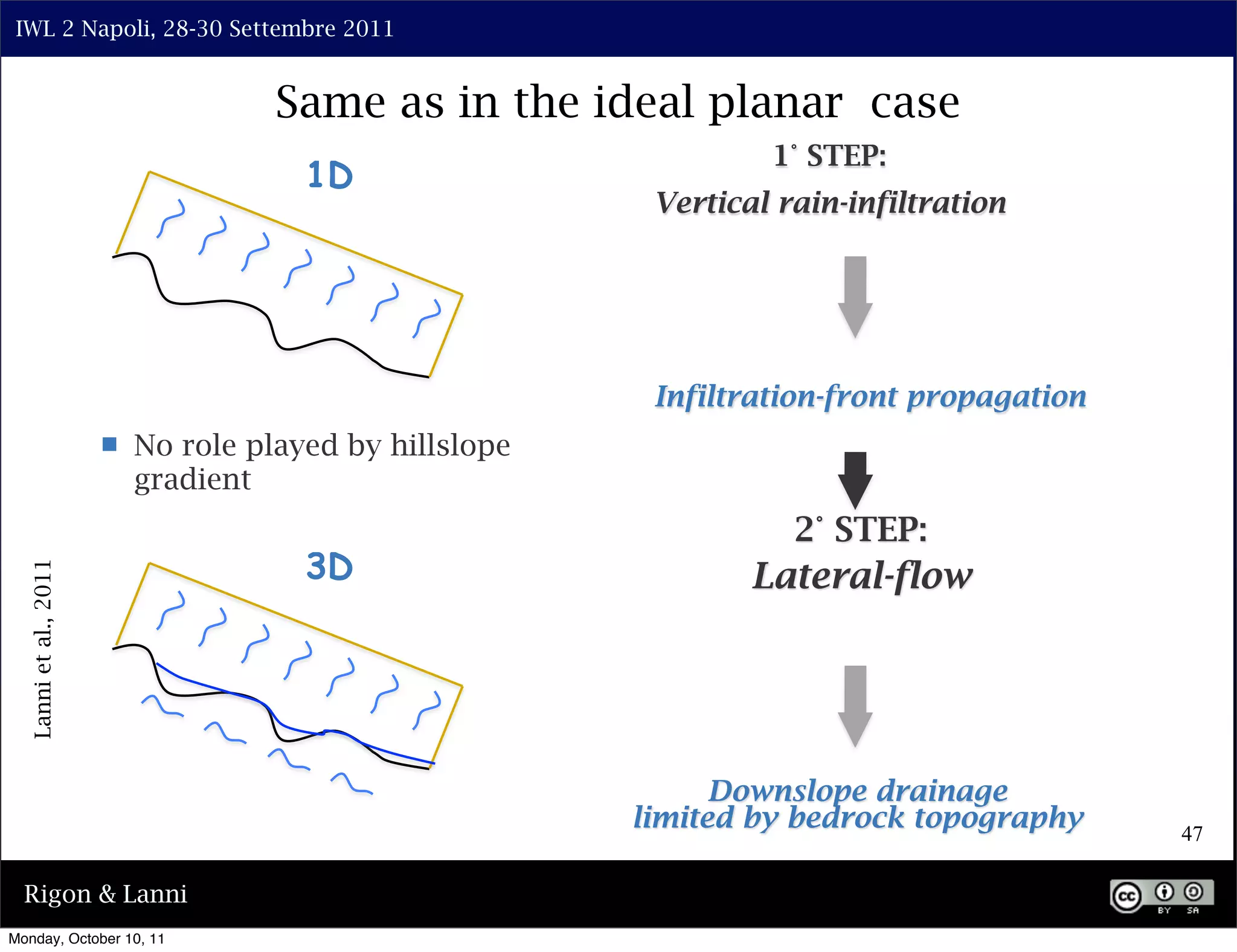
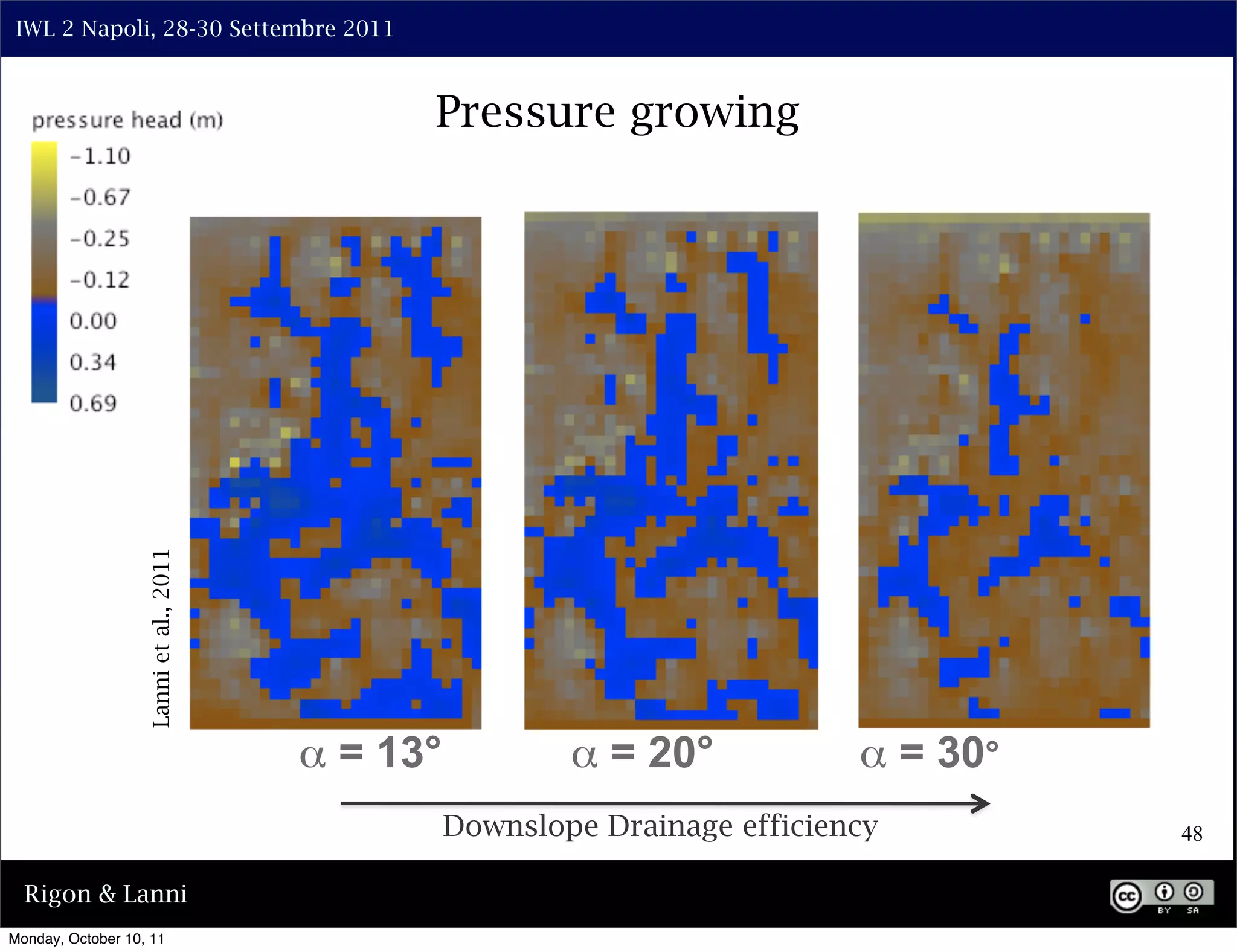
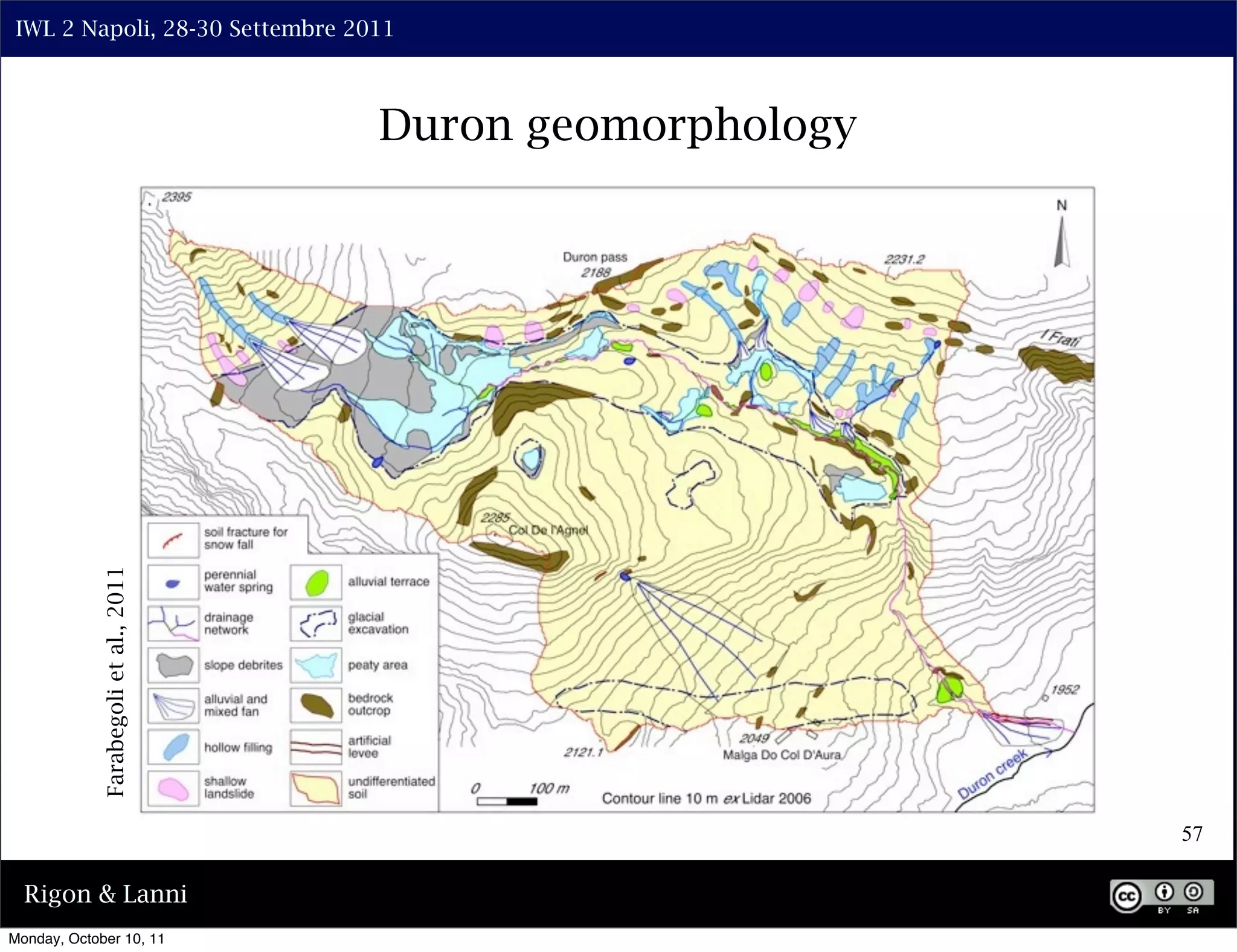
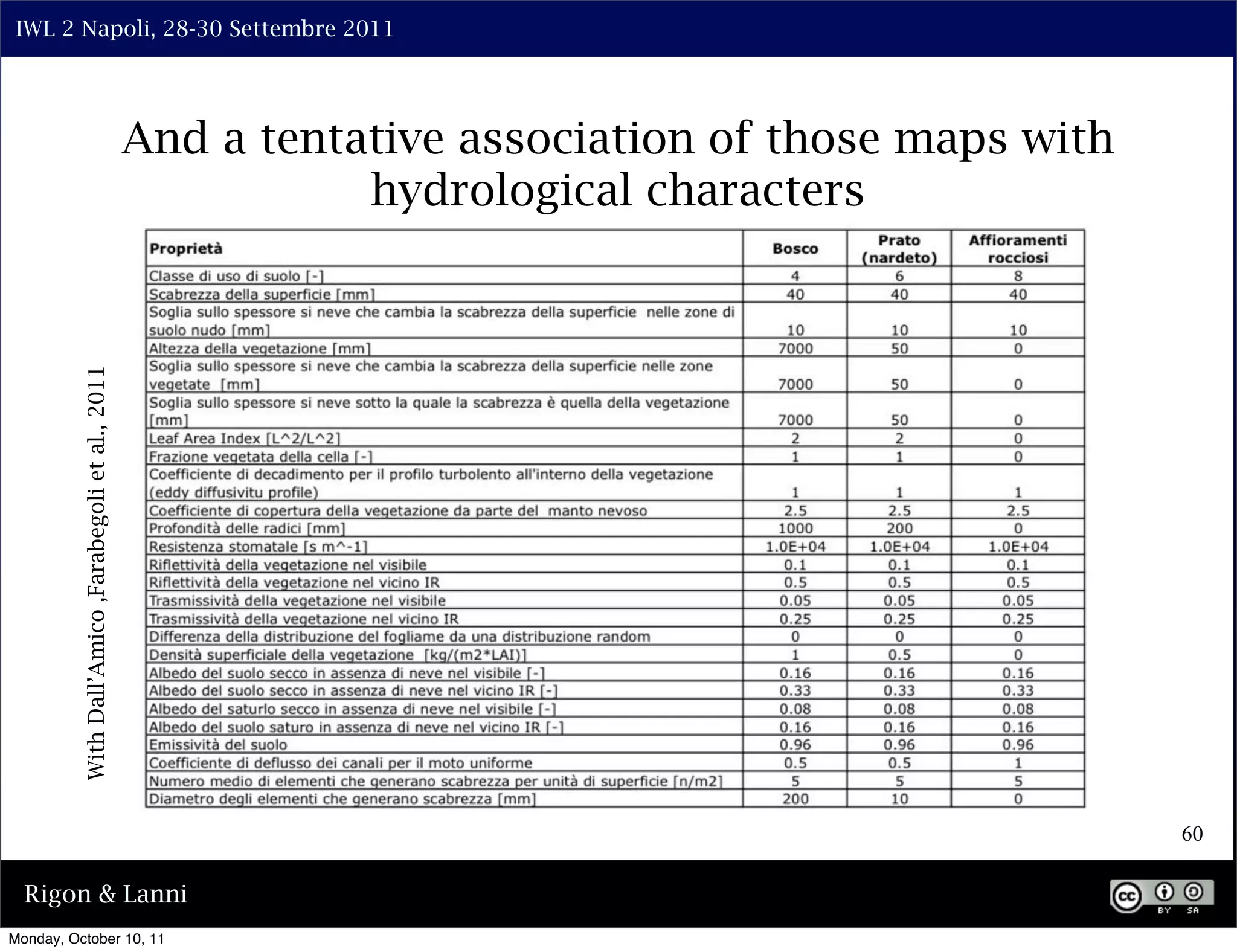
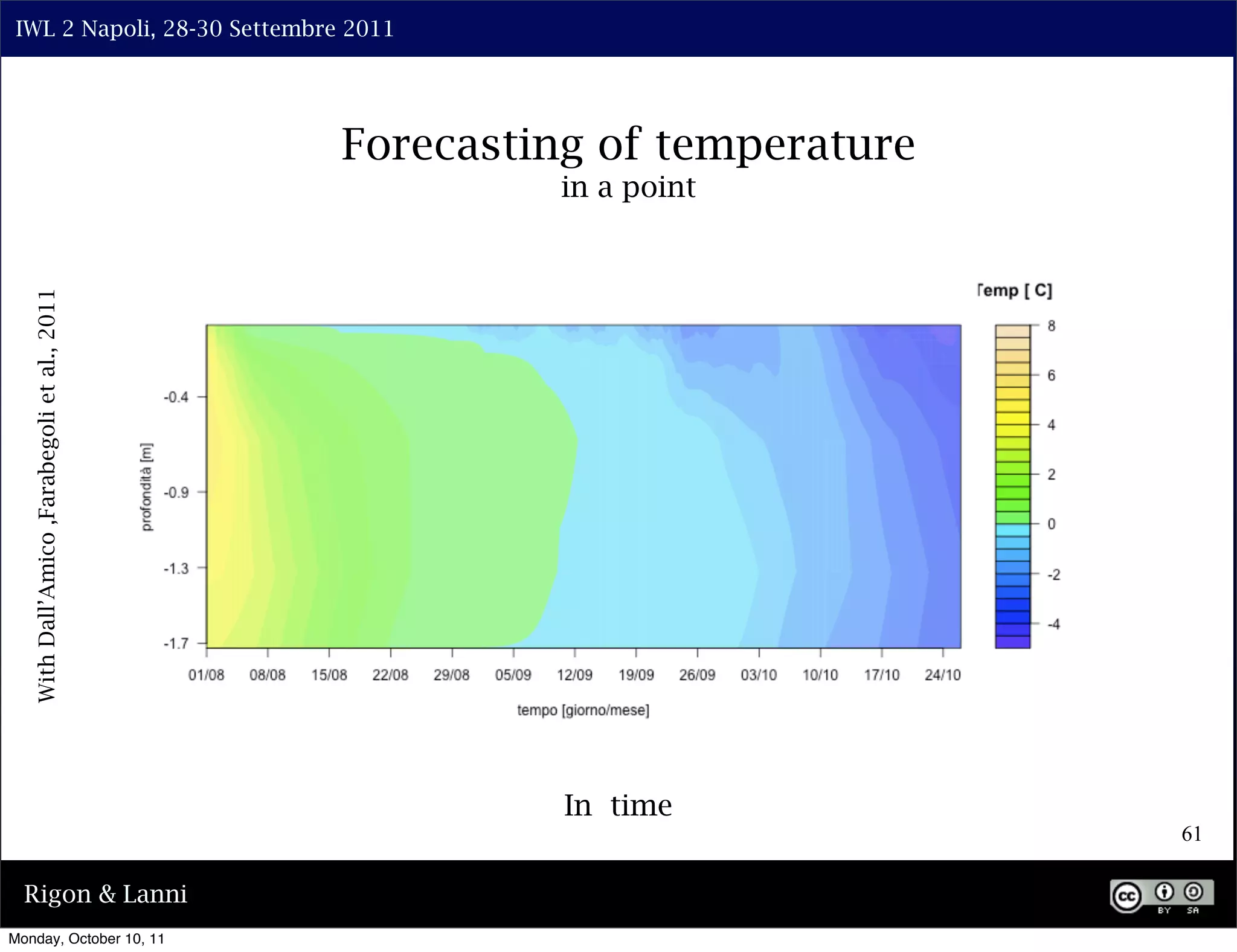
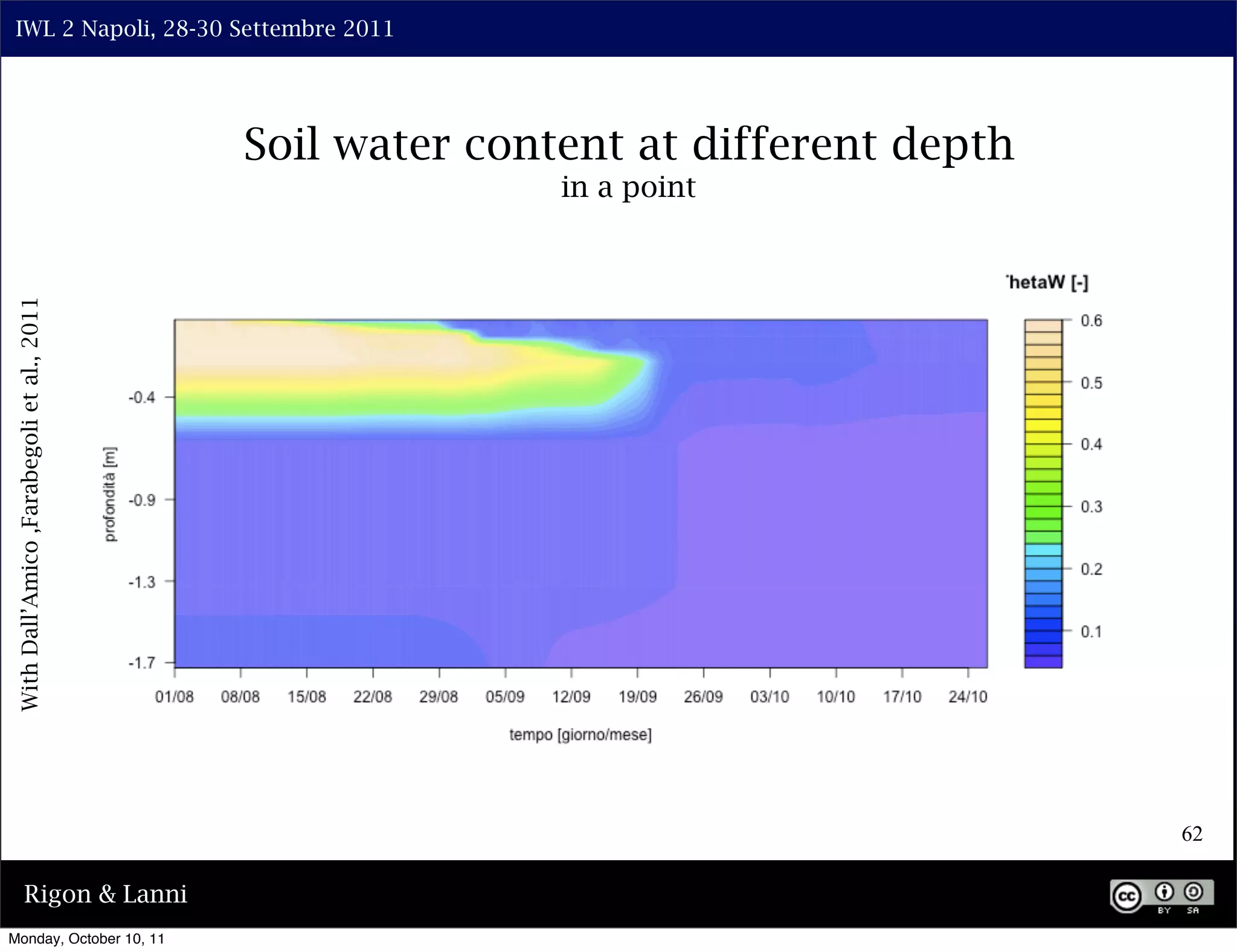
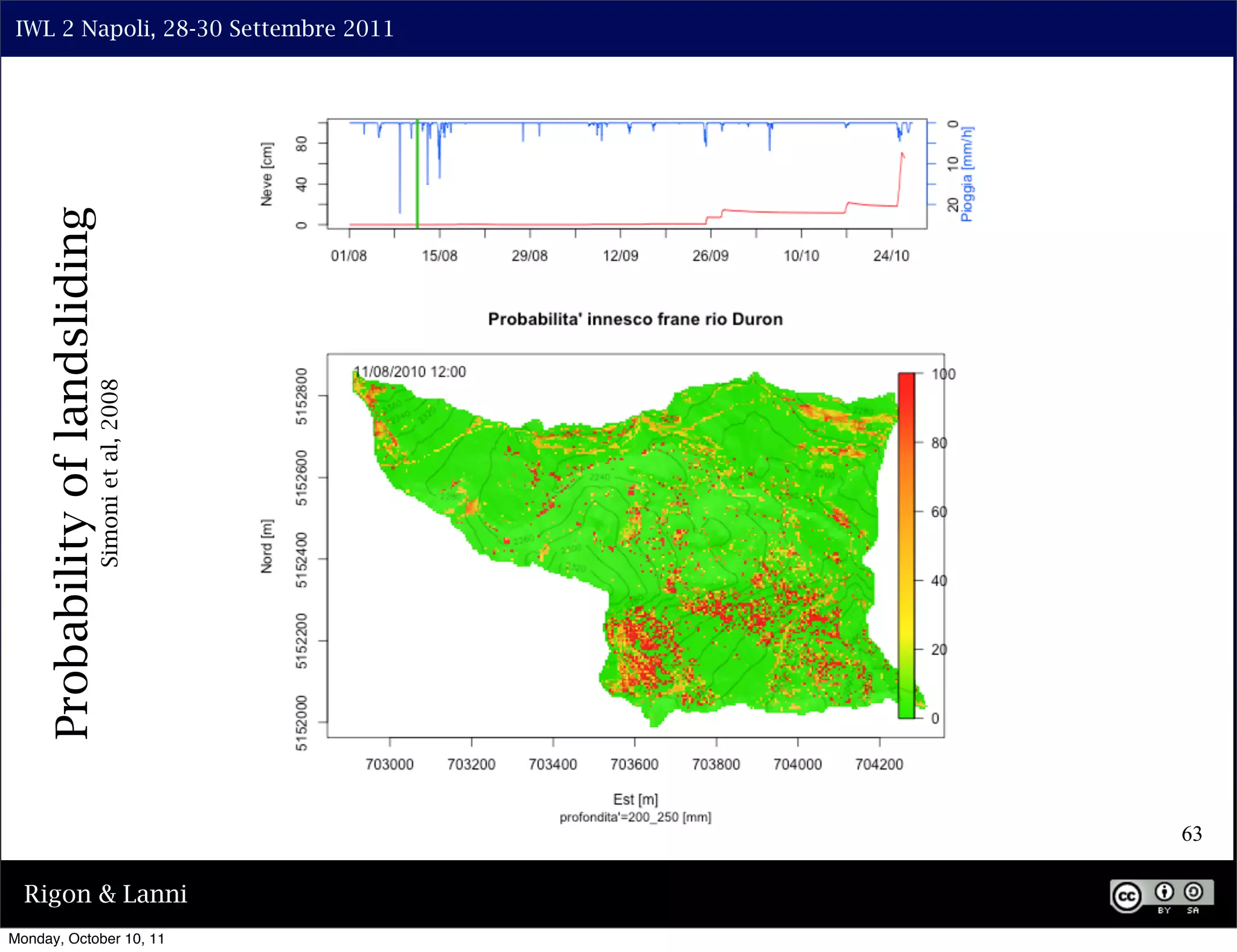
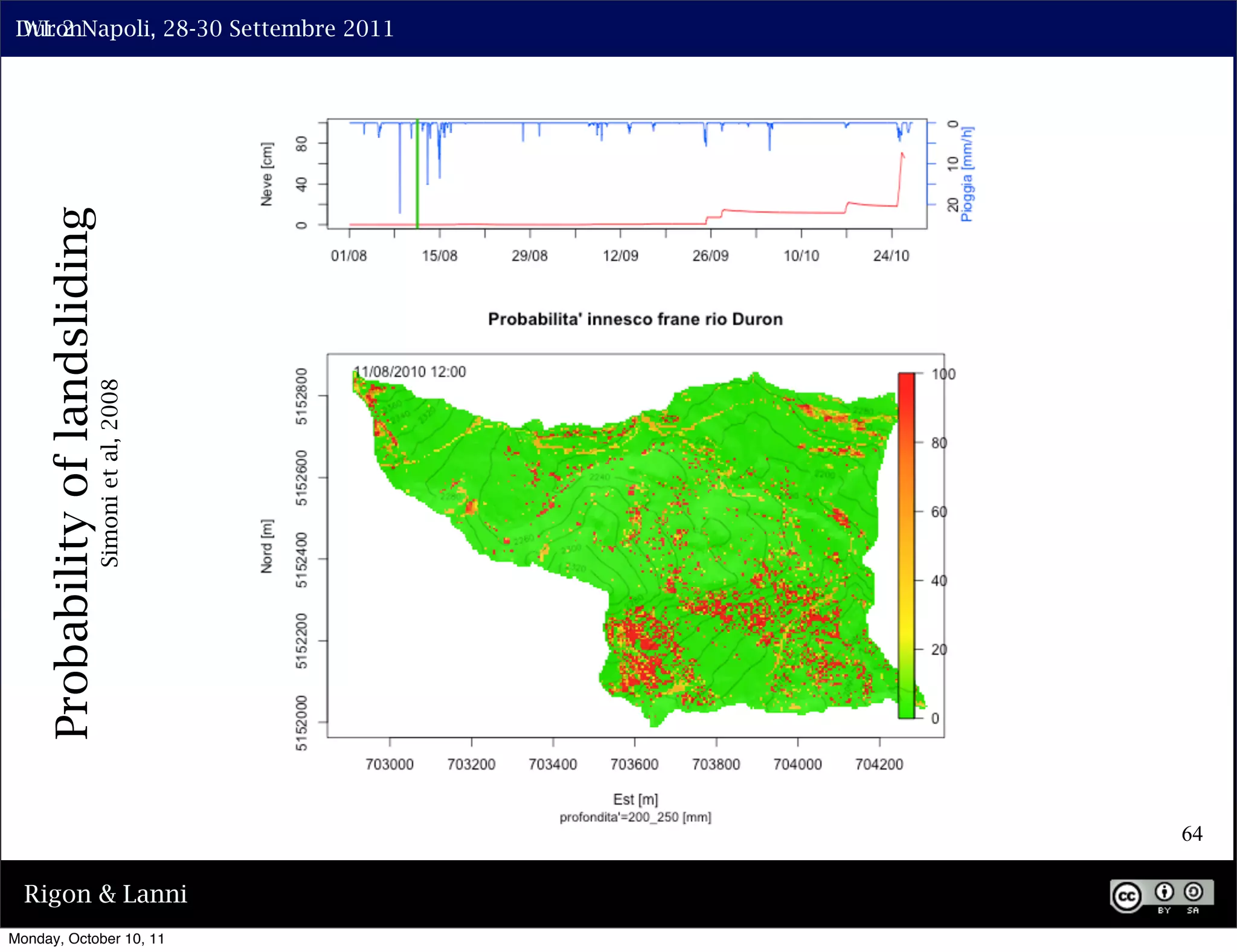
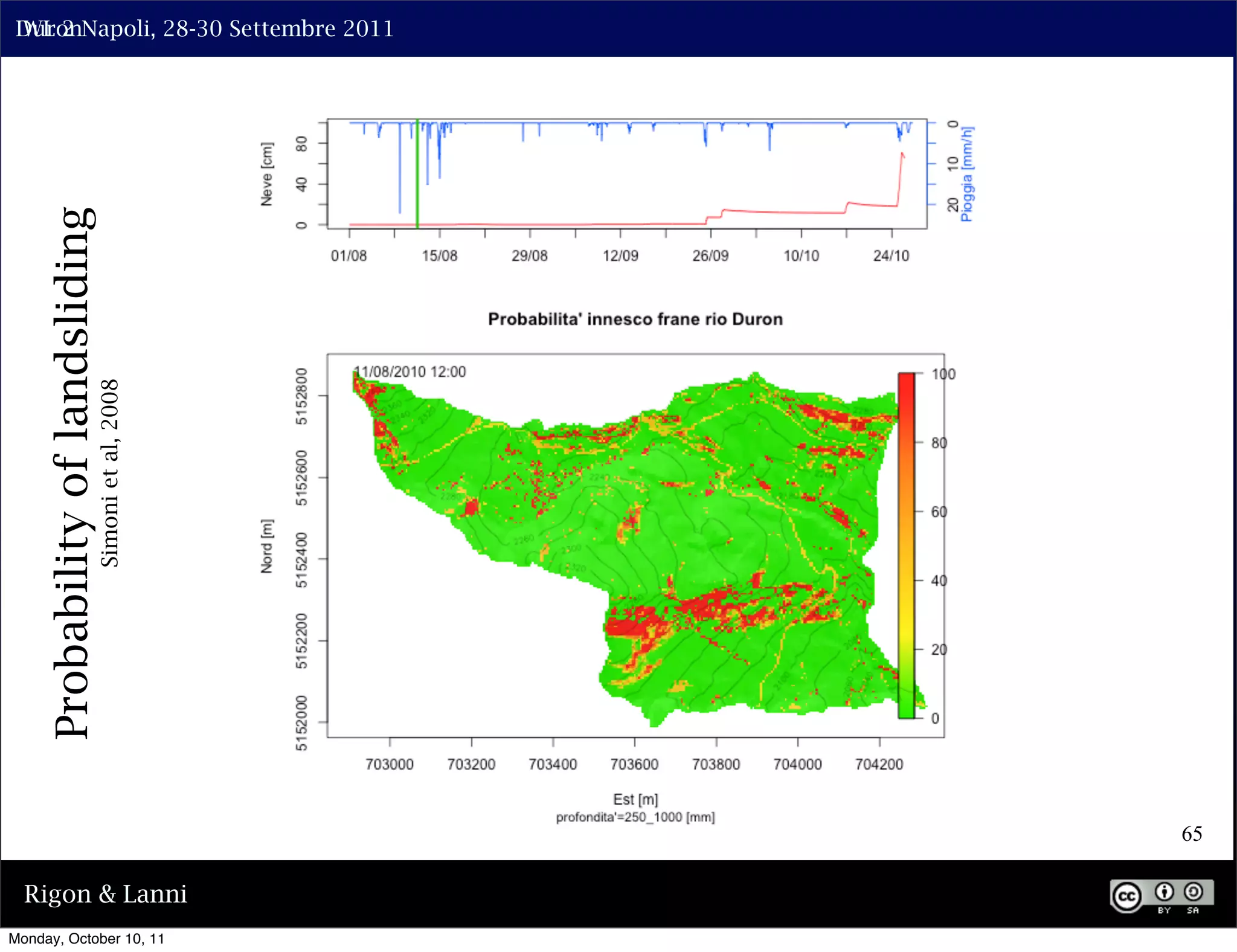
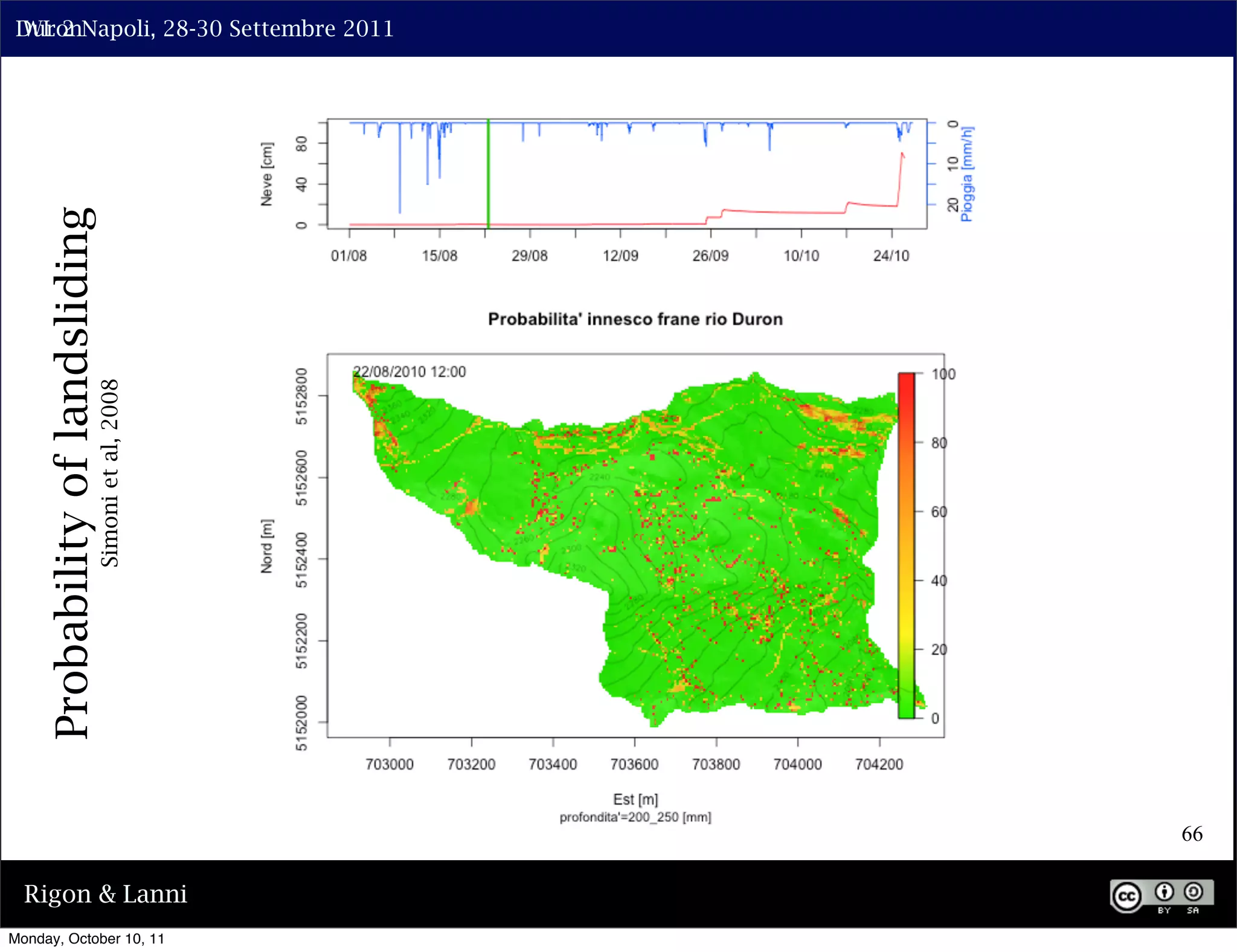
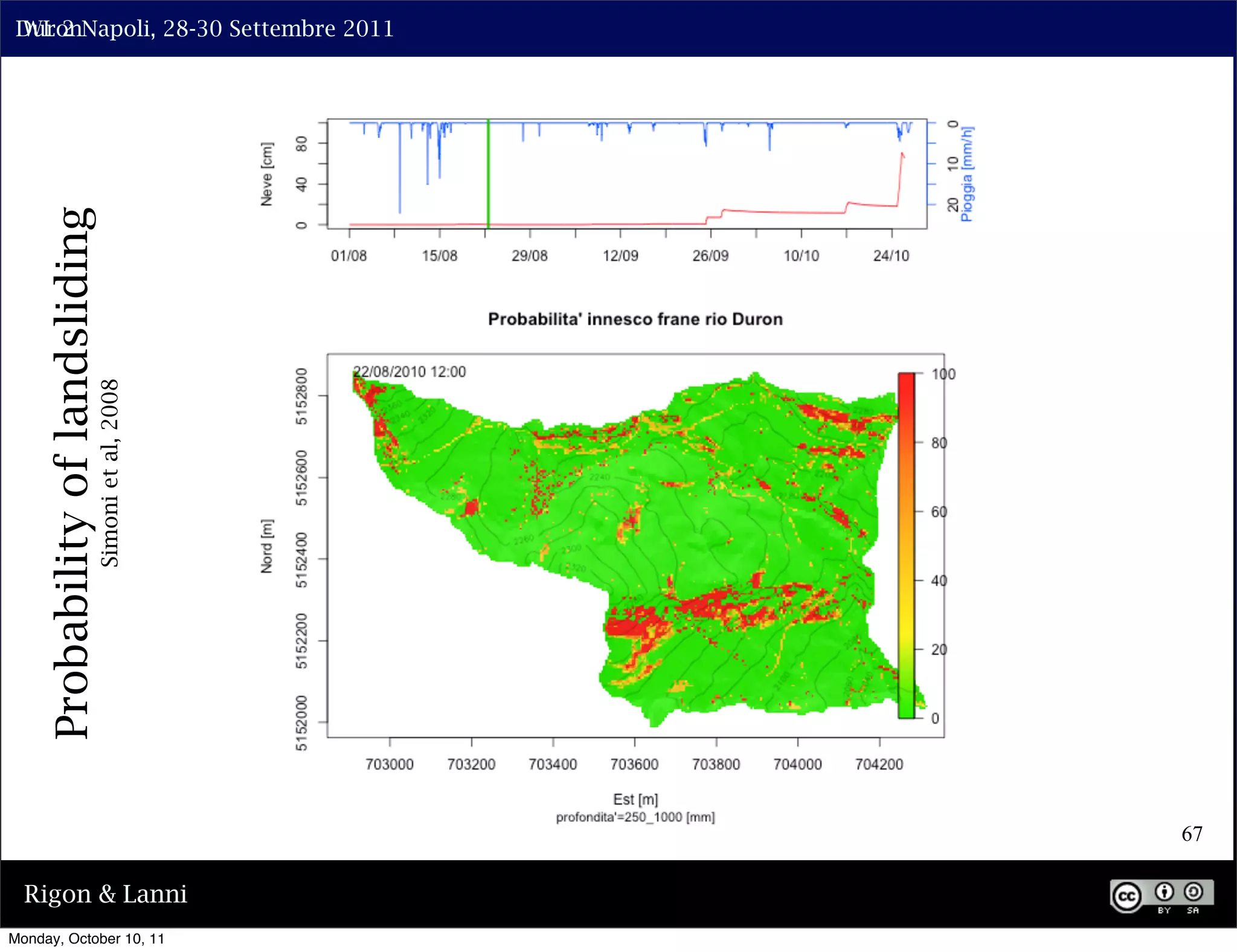
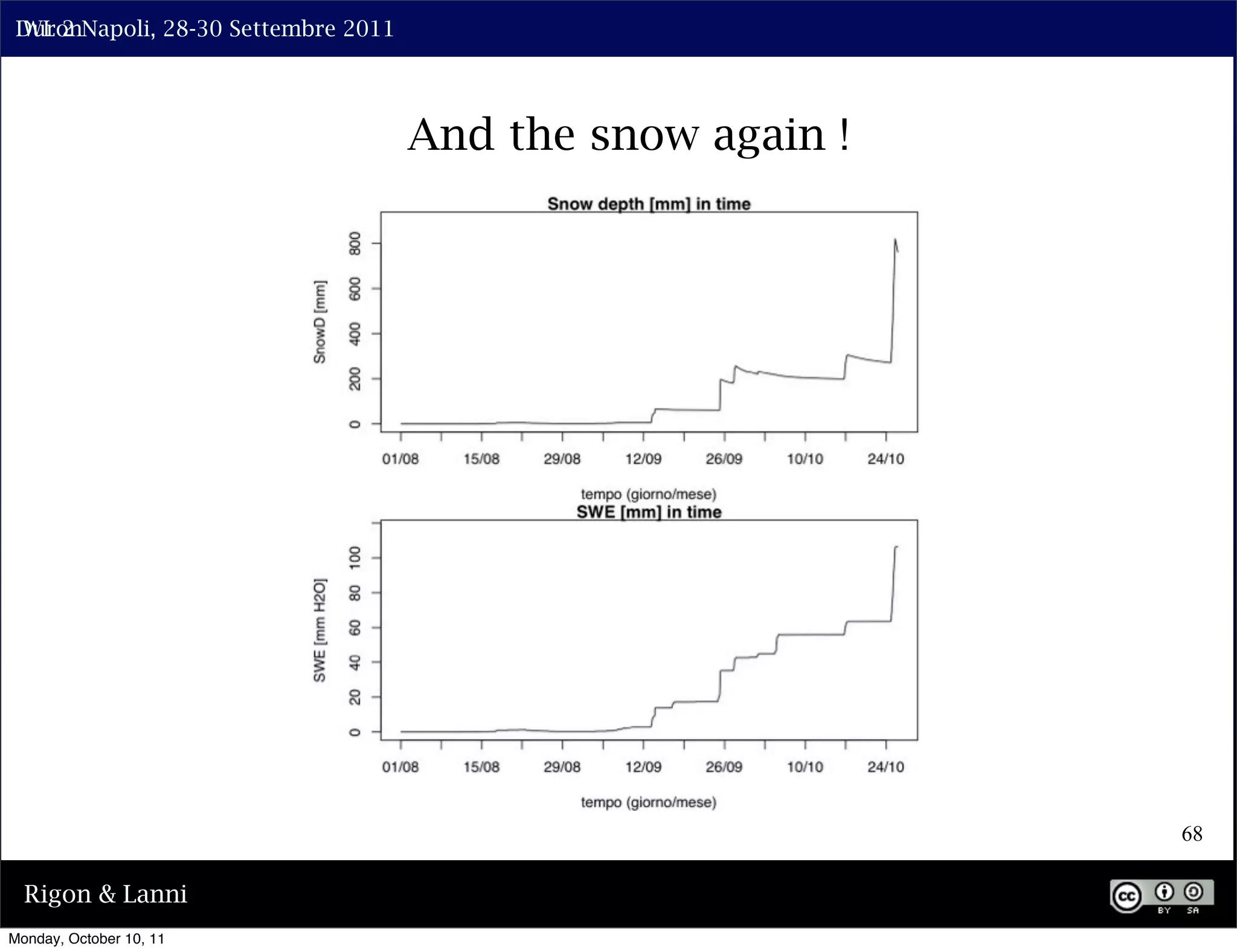
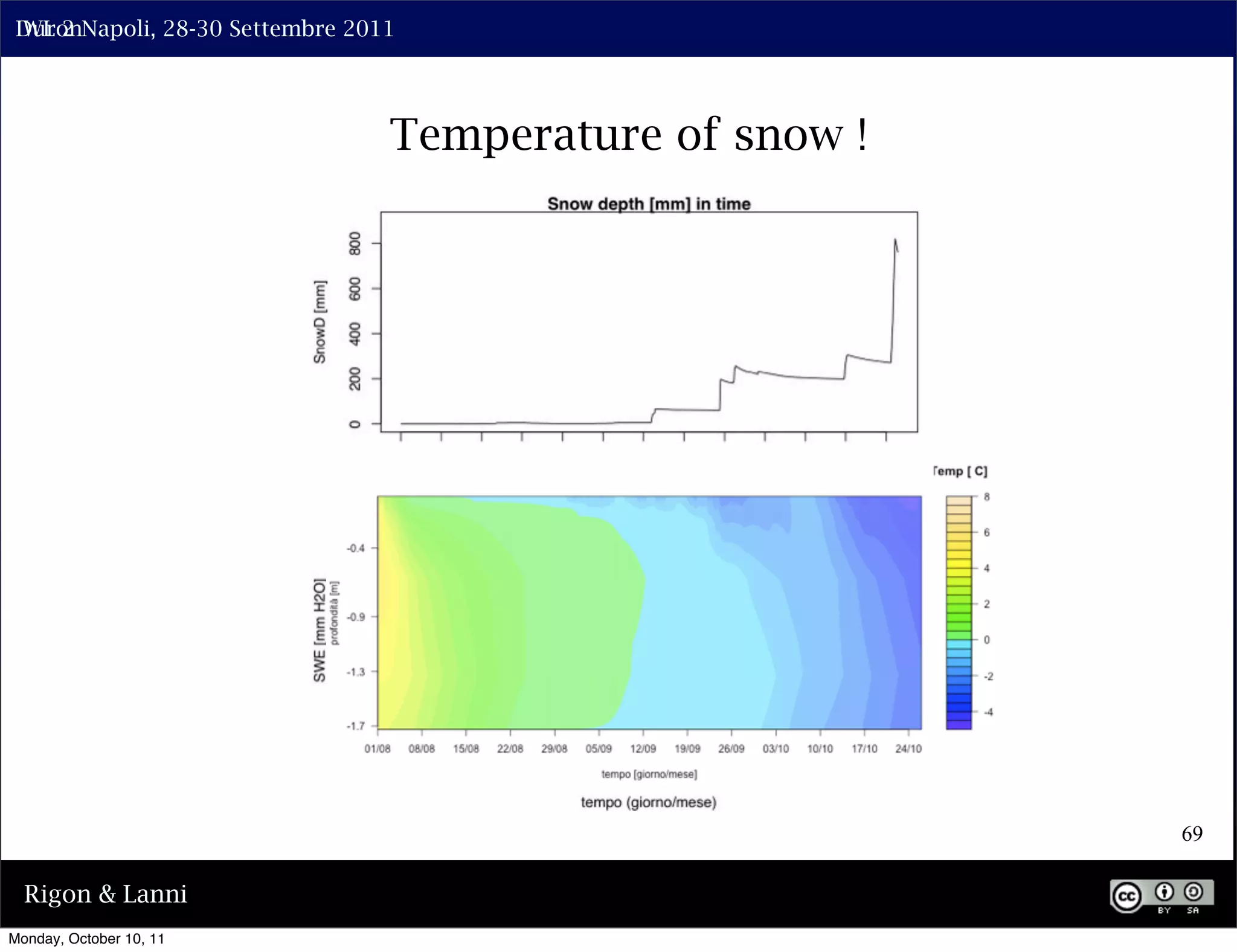
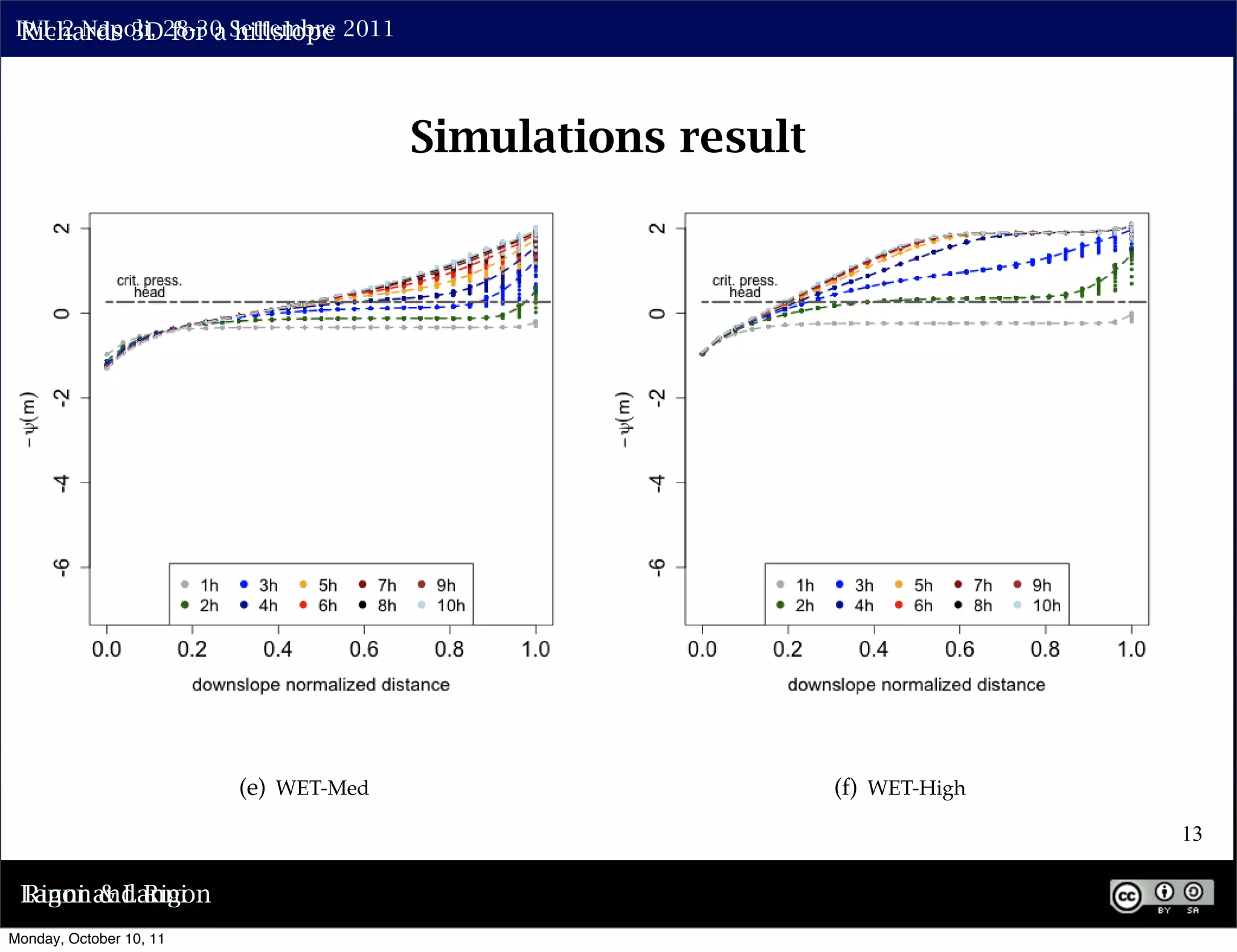
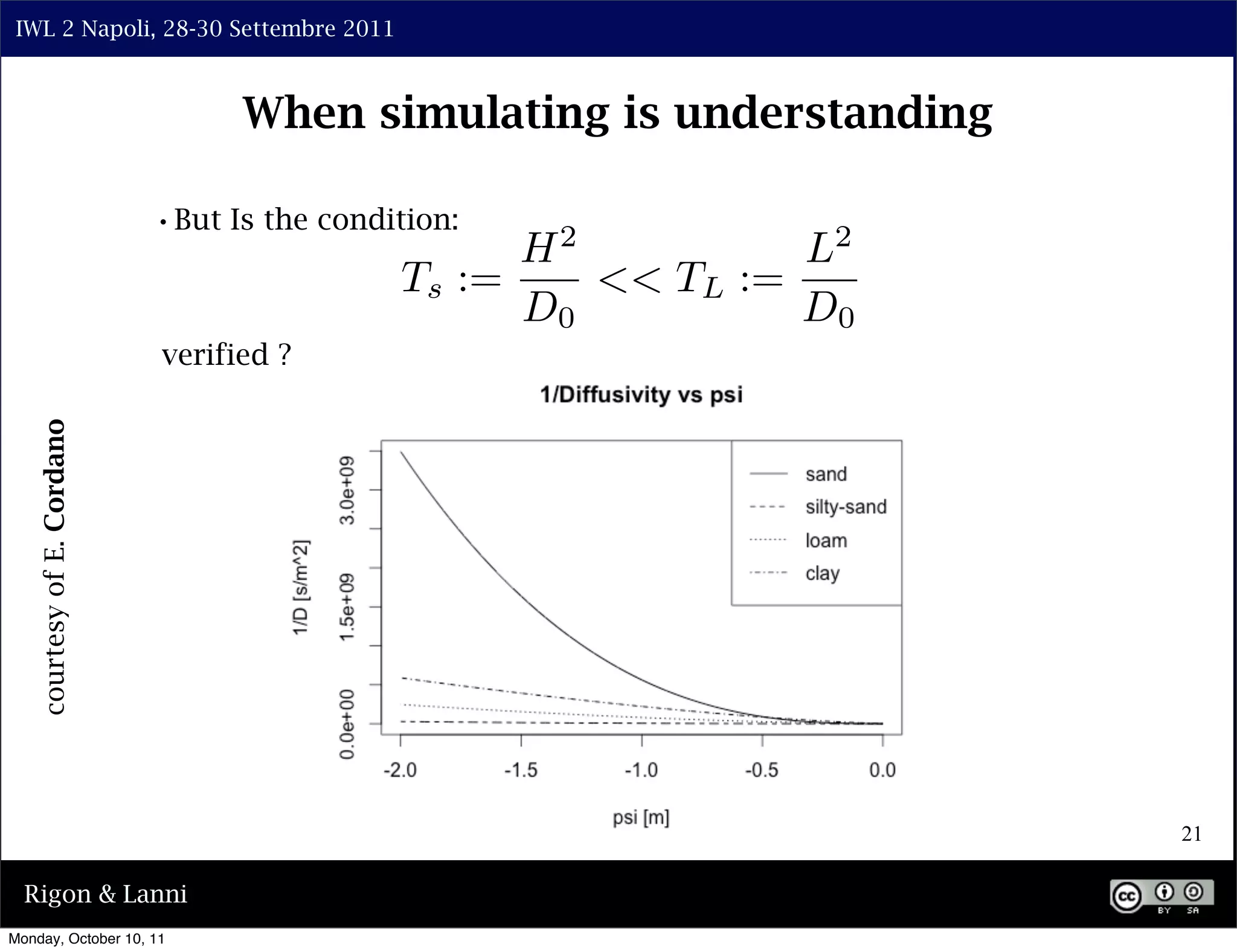
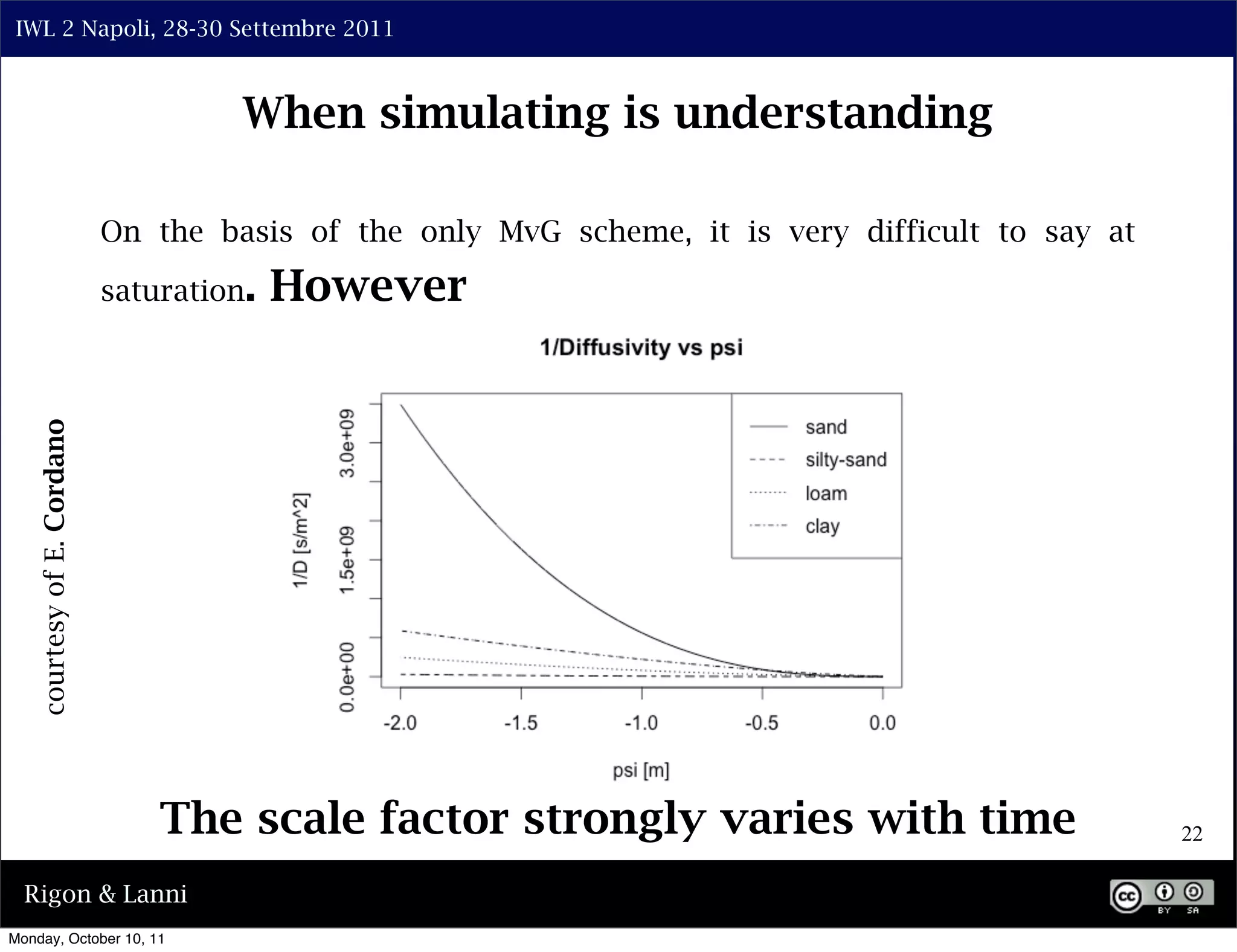
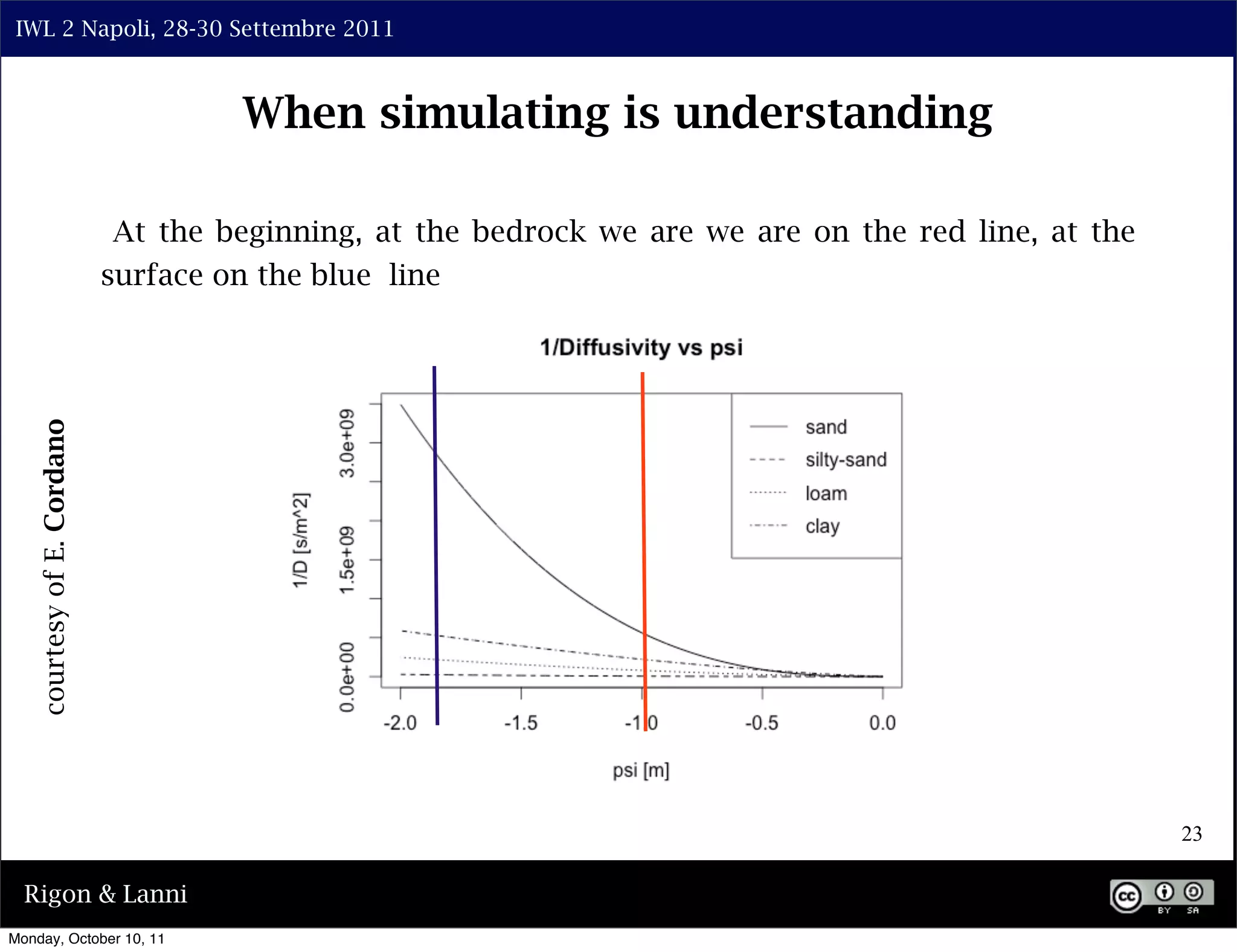
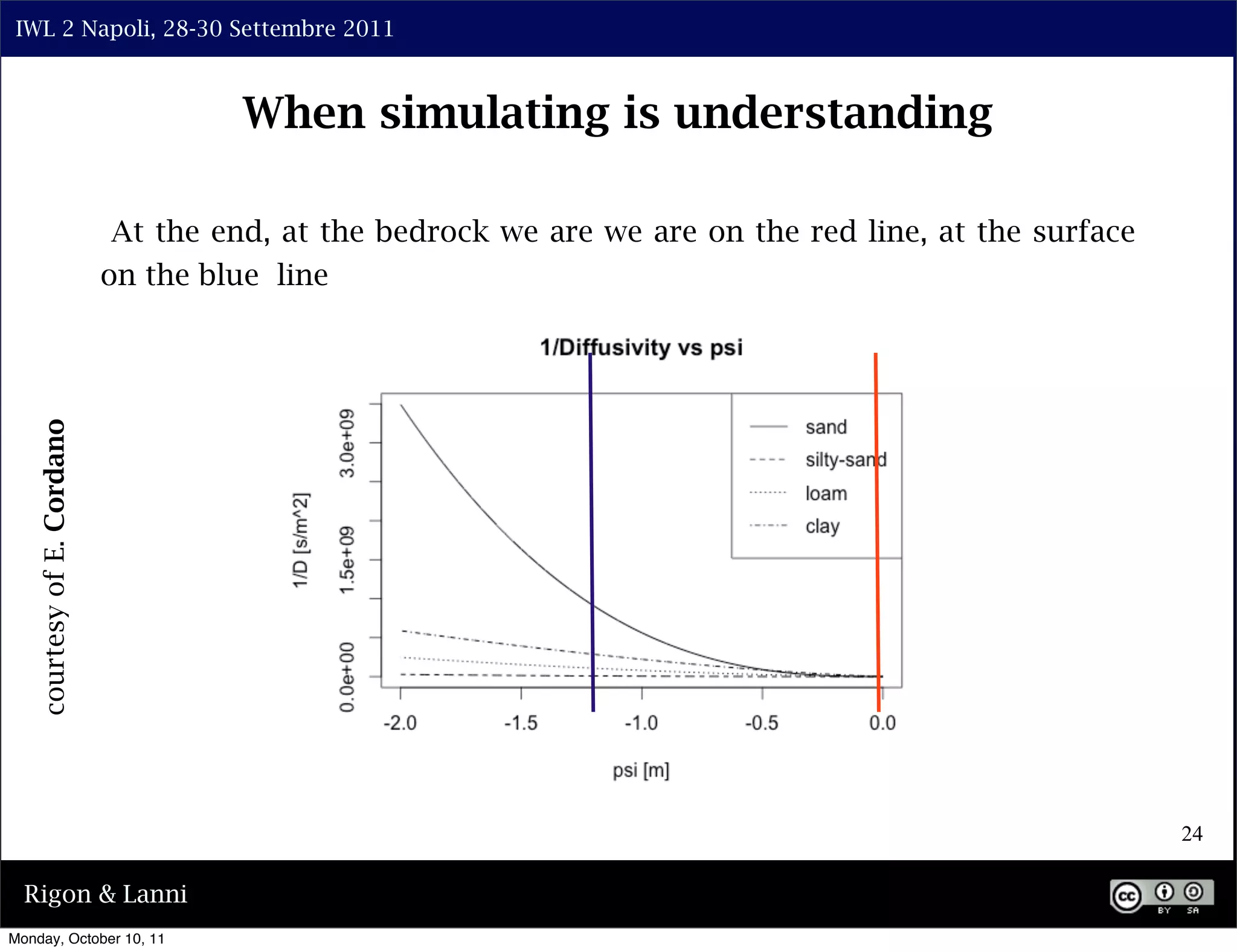
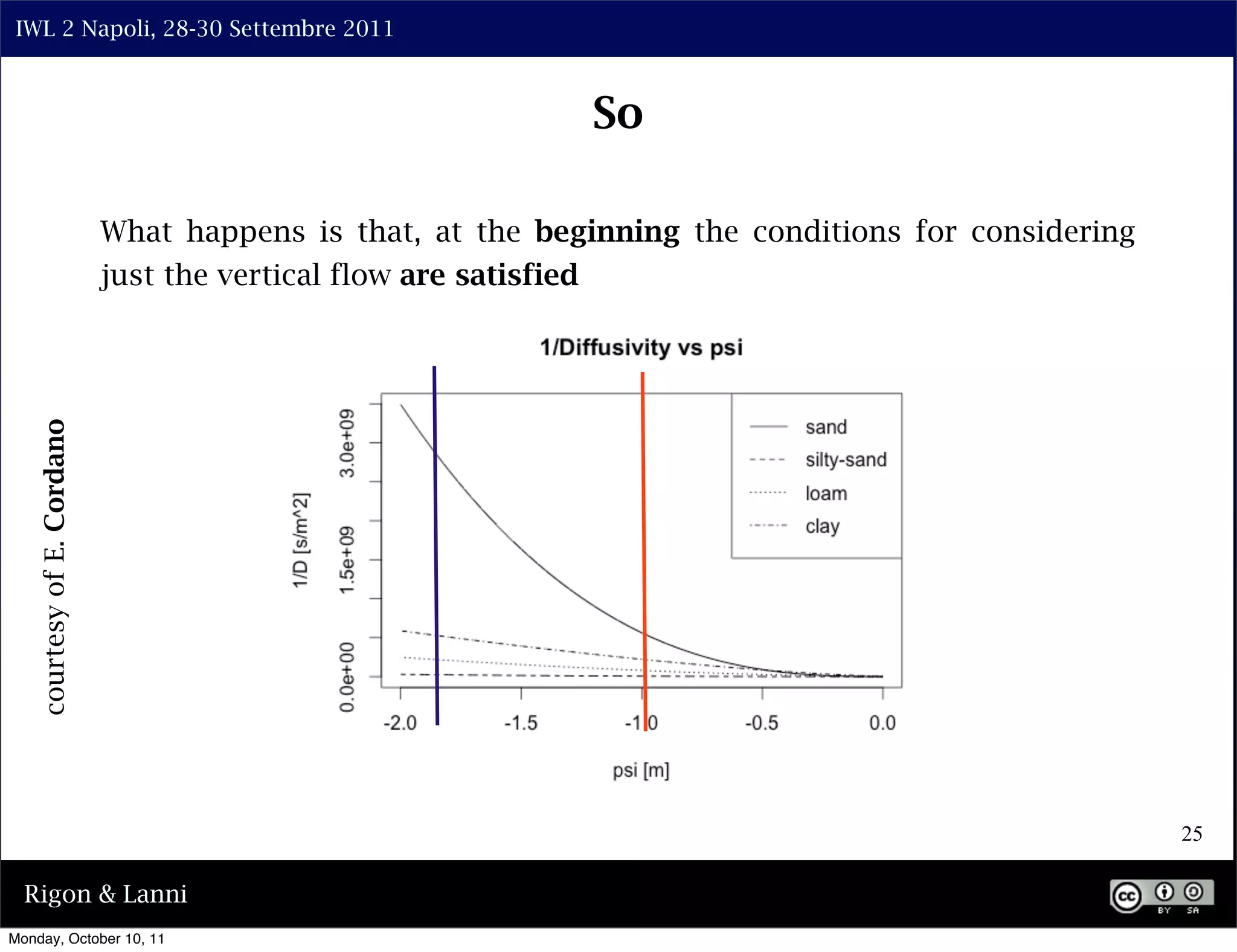
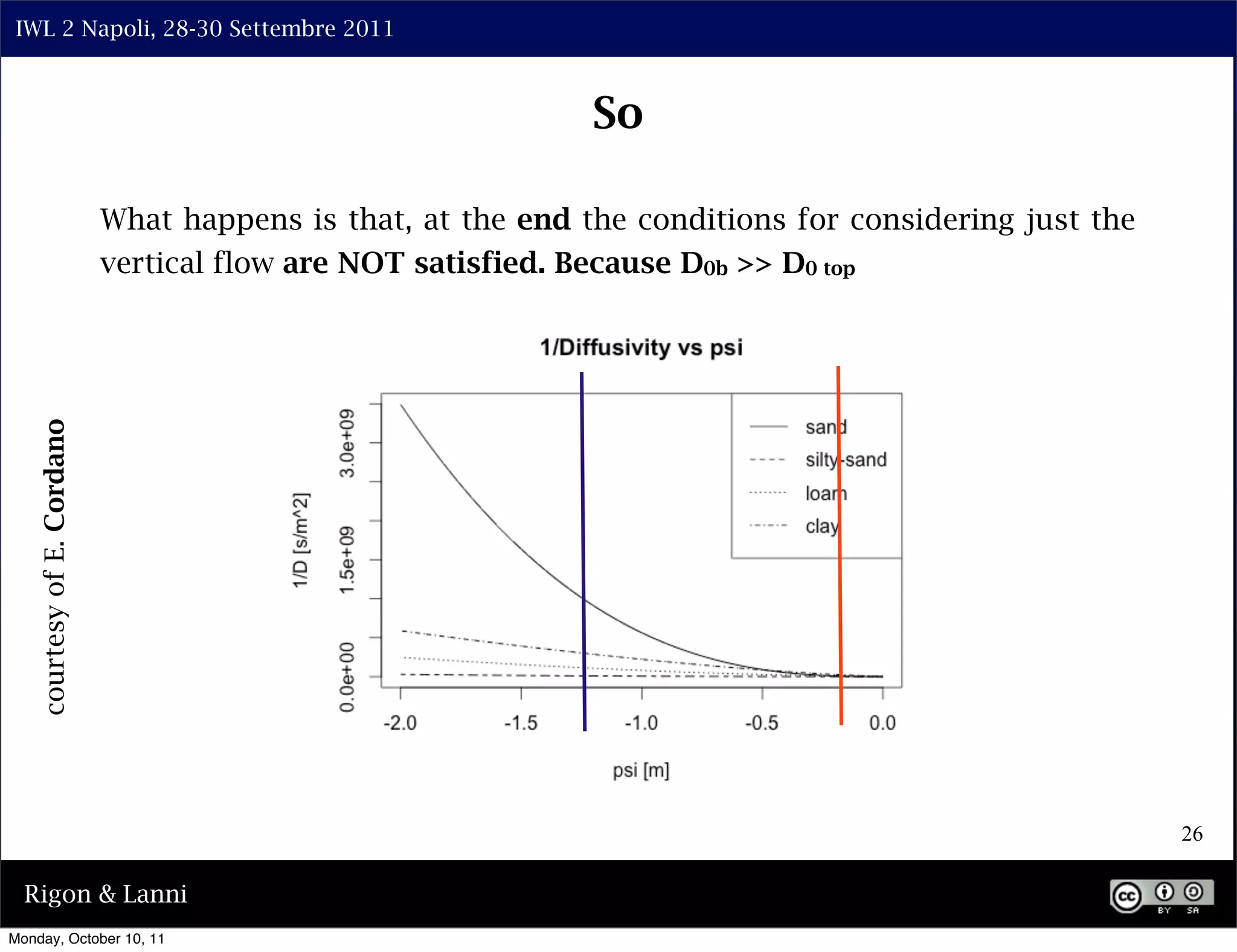
The document discusses the complexities of modeling hillslope hydrology and shallow landslides, focusing on the Richard's equation and its variants. It emphasizes the necessity to reconsider parameterizations related to water flow and soil stability, highlighting aspects of vertical and lateral flow dynamics. The authors propose that better understanding and accurate modeling are crucial for predicting landslide triggers effectively.



![IWL 2 Napoli, 28-30 Settembre 2011
Richards
First, I would say, it means that it would be better to call it, for
instance: Richards-Mualem-vanGenuchten equation, since it is:
⇤⇥ ⇥
C(⇥) = ⇥ · K( w ) ⇥ (z + ⇥)
⇤t
n
Se = [1 + ( ⇥) )] m
⇧ ⇤ ⇥ m ⌅2
w) = Ks 1 (1 Se ) 1/m
K( Se
⇤ w () w r
C(⇥) := Se :=
⇤⇥ ⇥s r
4
Rigon & Lanni
Monday, October 10, 11](https://image.slidesharecdn.com/iwl2rigonlanni-111002162853-phpapp01/75/Presentation-given-at-the-second-I-4-2048.jpg)
![IWL 2 Napoli, 28-30 Settembre 2011
Richards
First, I would say, it means that it would be better to call it, for
instance: Richards-Mualem-vanGenuchten equation, since it is:
⇤⇥ ⇥
C(⇥) = ⇥ · K( w ) ⇥ (z + ⇥) Water balance
⇤t
n
Se = [1 + ( ⇥) )] m
⇧ ⇤ ⇥ m ⌅2
w) = Ks 1 (1 Se ) 1/m
K( Se
⇤ w () w r
C(⇥) := Se :=
⇤⇥ ⇥s r
4
Rigon & Lanni
Monday, October 10, 11](https://image.slidesharecdn.com/iwl2rigonlanni-111002162853-phpapp01/75/Presentation-given-at-the-second-I-5-2048.jpg)
![IWL 2 Napoli, 28-30 Settembre 2011
Richards
First, I would say, it means that it would be better to call it, for
instance: Richards-Mualem-vanGenuchten equation, since it is:
⇤⇥ ⇥
C(⇥) = ⇥ · K( w ) ⇥ (z + ⇥) Water balance
⇤t
n
Se = [1 + ( ⇥) )] m
⇧ ⇤ ⇥ m ⌅2 Parametric
w) = Ks 1 (1 Se ) 1/m
K( Se Mualem
⇤ w () w r
C(⇥) := Se :=
⇤⇥ ⇥s r
4
Rigon & Lanni
Monday, October 10, 11](https://image.slidesharecdn.com/iwl2rigonlanni-111002162853-phpapp01/75/Presentation-given-at-the-second-I-6-2048.jpg)
![IWL 2 Napoli, 28-30 Settembre 2011
Richards
First, I would say, it means that it would be better to call it, for
instance: Richards-Mualem-vanGenuchten equation, since it is:
⇤⇥ ⇥
C(⇥) = ⇥ · K( w ) ⇥ (z + ⇥) Water balance
⇤t
n
Se = [1 + ( ⇥) )] m Parametric
van Genuchten
⇧ ⇤ ⇥ m ⌅2 Parametric
w) = Ks 1 (1 Se ) 1/m
K( Se Mualem
⇤ w () w r
C(⇥) := Se :=
⇤⇥ ⇥s r
4
Rigon & Lanni
Monday, October 10, 11](https://image.slidesharecdn.com/iwl2rigonlanni-111002162853-phpapp01/75/Presentation-given-at-the-second-I-7-2048.jpg)

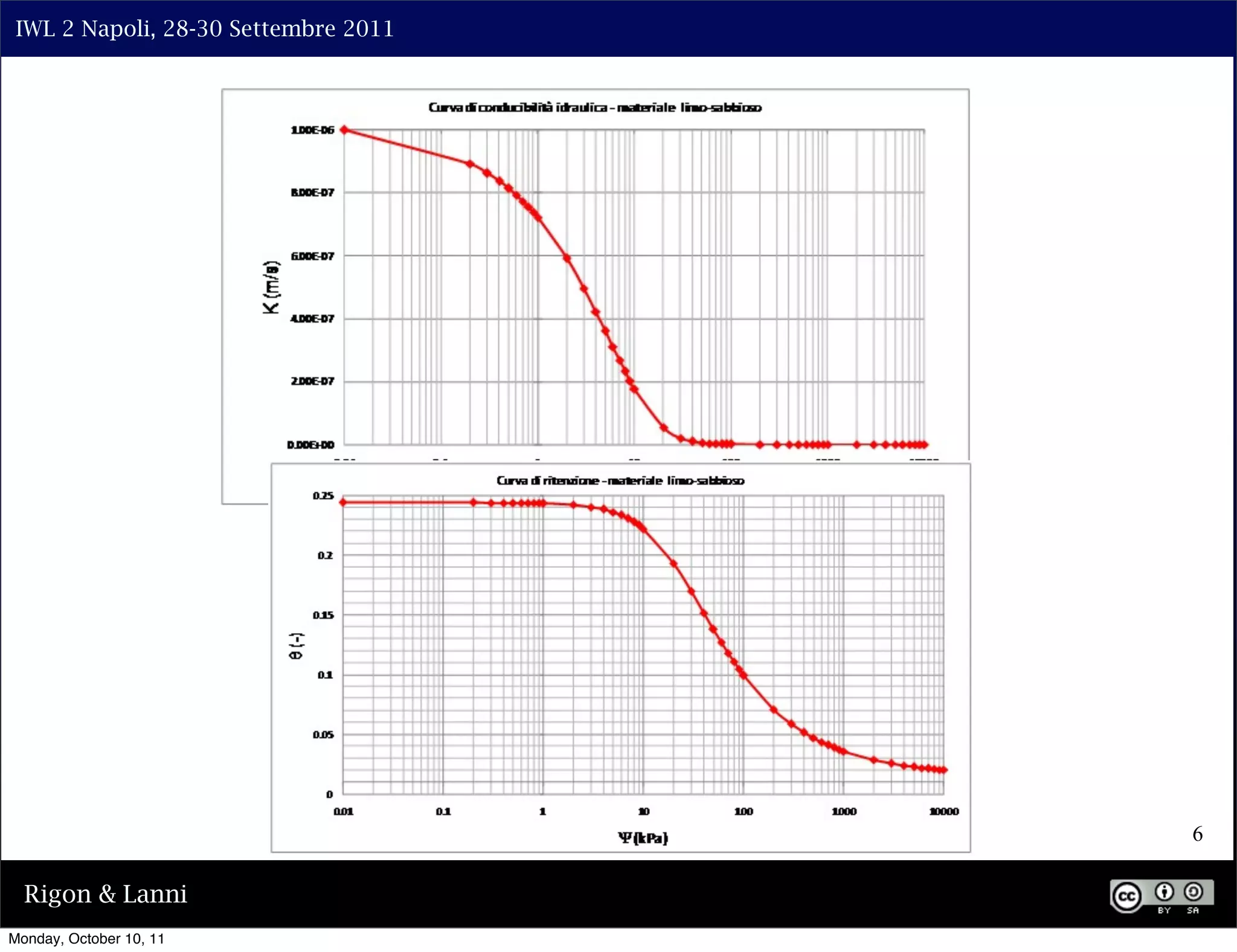
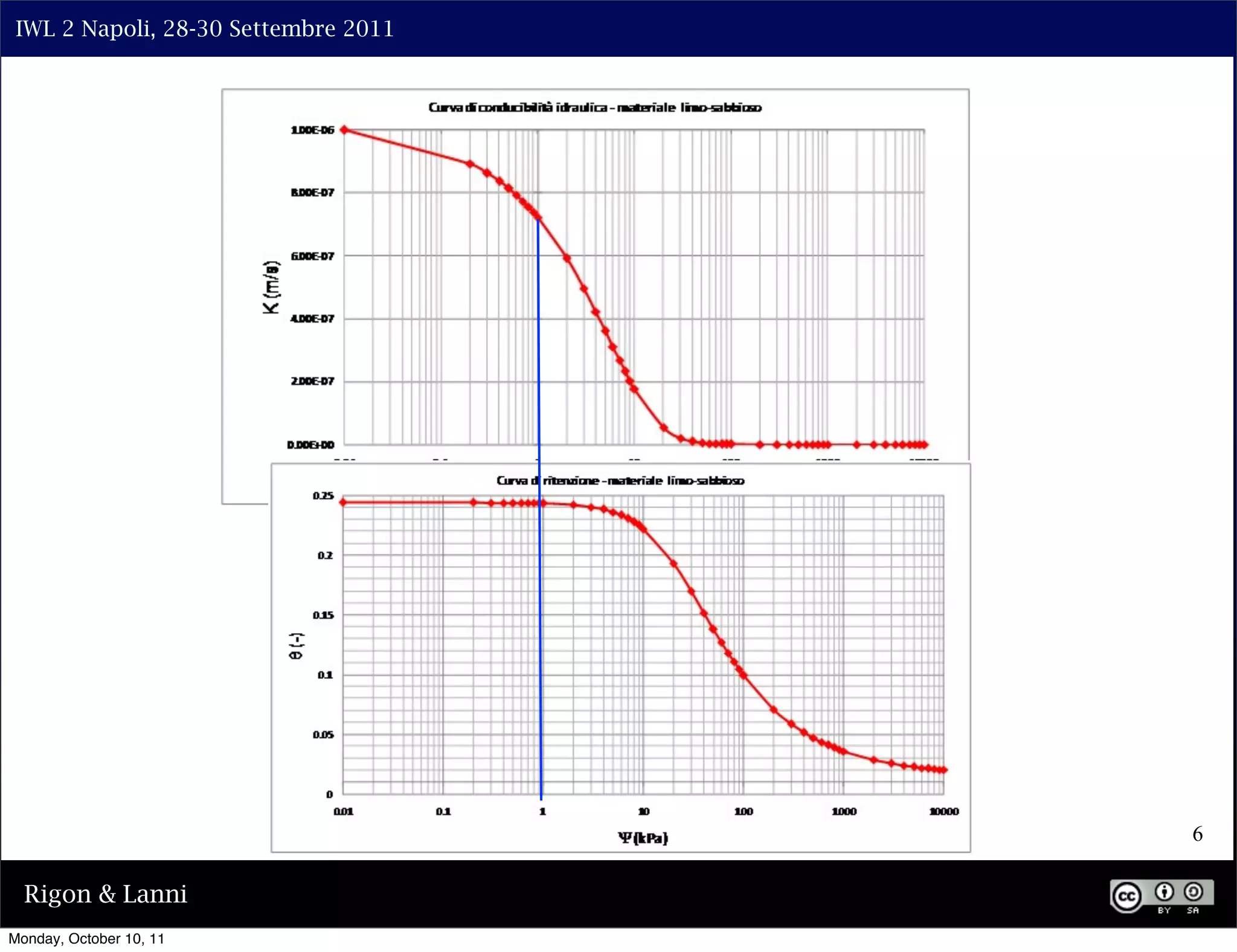
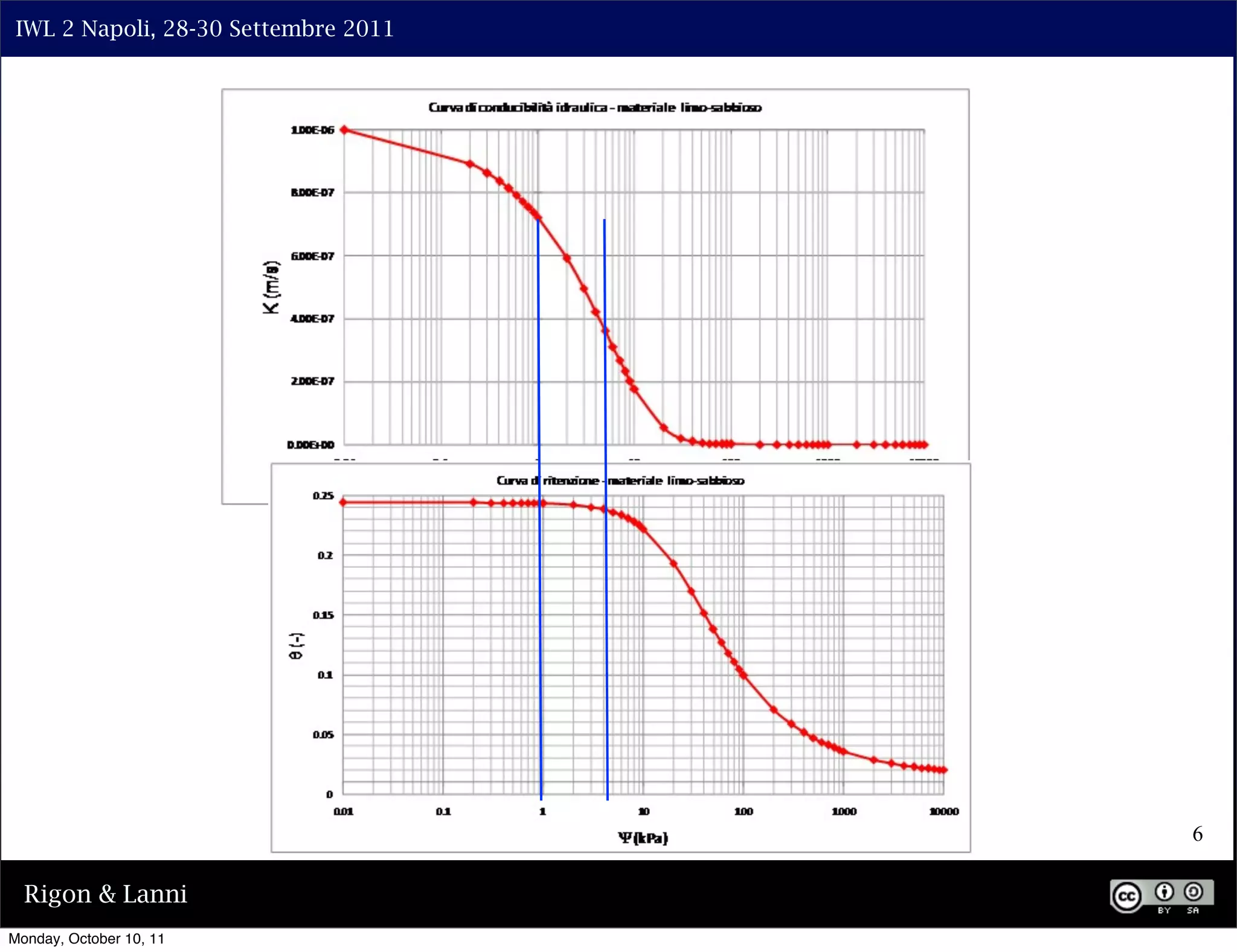
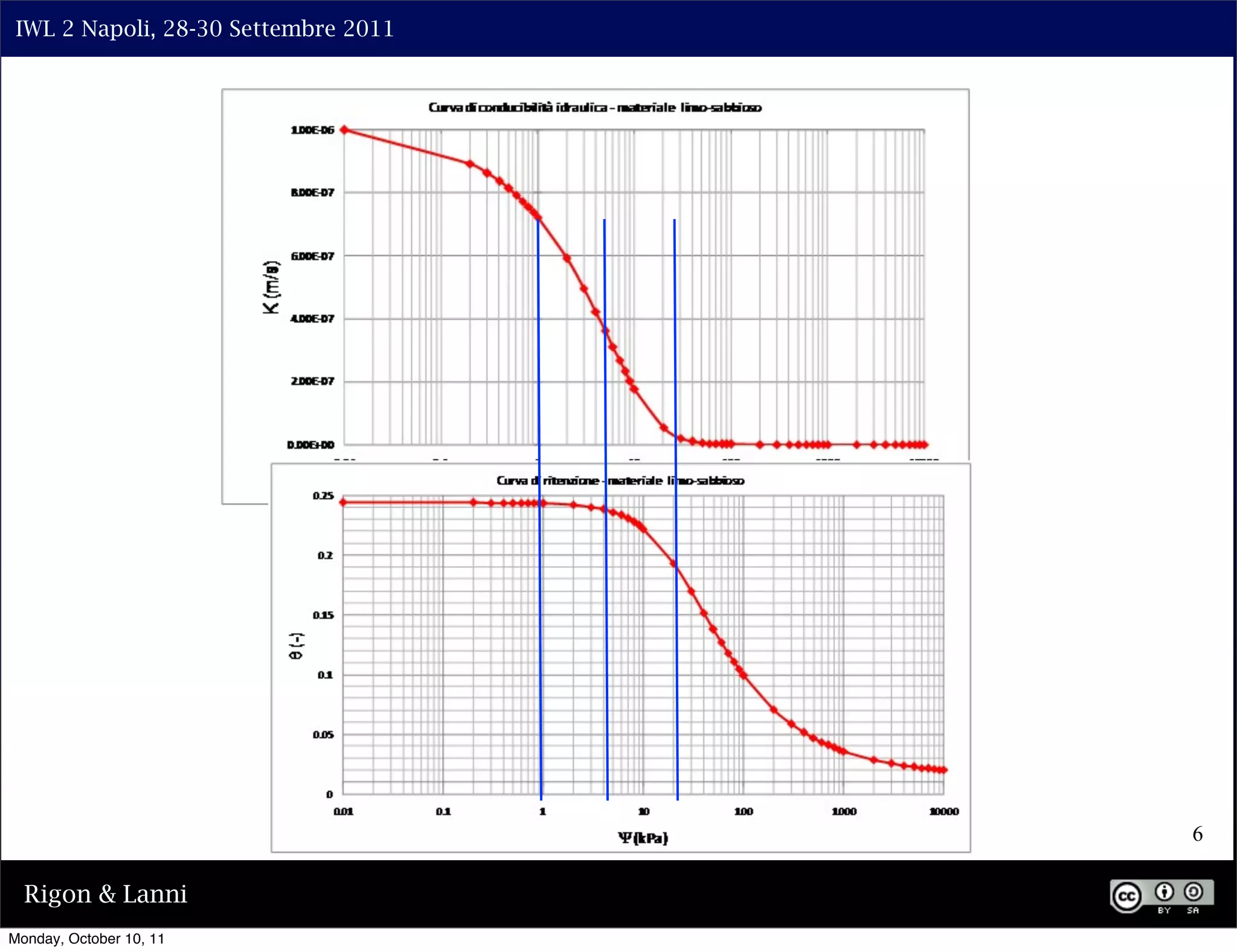
















![IWL 2 Napoli, 28-30 Settembre 2011
PARAMETRIC FORMS OF THE
HYDRAULIC CONDUCTIVITY
there results:
⇤ ⇥m ⌅2
K(Se ) = v
K s Se 1 1 1/m
Se (m = 1 1/n)
or, by expressing everything as a function of the suction
potential:
⇥2
mn n m
Ks 1 ( ⇥) [1 + ( ⇥) ]
K(⇥) = n mv (m = 1 1/n)
[1 + ( ⇥) ]
30
Rigon & Lanni
Monday, October 10, 11](https://image.slidesharecdn.com/iwl2rigonlanni-111002162853-phpapp01/75/Presentation-given-at-the-second-I-40-2048.jpg)